
Concept explainers
The circuit parameters for the differential amplifier shown in Figure 11.2 are V+=5V,V−=−5V,IQ=0.3mA, and RC=20kΩ. The transistor Parameters are β=180,VBE(on)=0.7V, and VA=∞. Determine the voltages vE,vC1,vC2,vCE1, and vCE2 for (a)v1=v2=0,(b) v1=v2=−1V and (c) v1=v2=+1 V. (Ans. (a) vE=−0.7V,vC1=vC2=2V,vCE1= vCE2=2.7V; (b) vE=−1.7V, vC1=vC2=2V, vCE1=vCE2=3.7V (c) vE=+0.3V,vC1=vC2=2V,vCE1=vCE2=1.7V) .
a.
The collector voltages, collector to emitter voltages and the emitter voltage for the given input values of a differential amplifier.
Answer to Problem 11.1EP
vE=−0.7 V , vC1=2 V , vC2=2 V , vCE1=2.7 V , vCE2=2.7 V
Explanation of Solution
Given Information:
The given values are:
V+=5 V, V−=−5 V,IQ=0.3 mA,RC=20 kΩ,β=180,VBE(on)=0.7 V,VA=∞v1=v2=0
The given circuit is shown below.
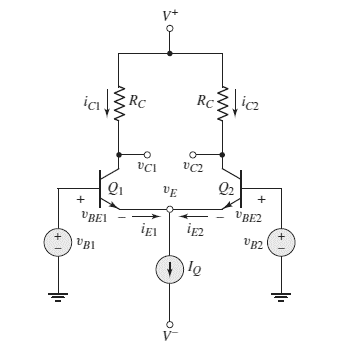
Calculation:
Voltage at emitter of each transistor
vE=0−VBE(on)
vE=−0.7 V
Assume transistors are matched. Then,
iE1=iE2=IQ2
Also assume that the bias currents are negligible. Then,
iC1≅iE1=IQ2,iC2≅=iE2=IQ2
Now
vC1=vC2=V+−IQ2RC=5−0.15×20 V
vC1=2 V, vC2=2 V
Then,
vCE1=vC1−vE=2−(−0.7)
vCE1=2.7 V
Similarly,
vCE2=vC2−vE=2−(−0.7)
vCE2=2.7 V
b.
The collector voltages, collector to emitter voltages and the emitter voltage for the given values of a differential amplifier.
Answer to Problem 11.1EP
vE=−1.7 V , vC1=2 V , vC2=2 V , vCE1=3.7 V , vCE2=3.7 V
Explanation of Solution
Given Information:
The given values are:
V+=5 V, V−=−5 V,IQ=0.3 mA,RC=20 kΩ,β=180,VBE(on)=0.7 V,VA=∞v1=v2=−1 V
The given circuit is shown below.
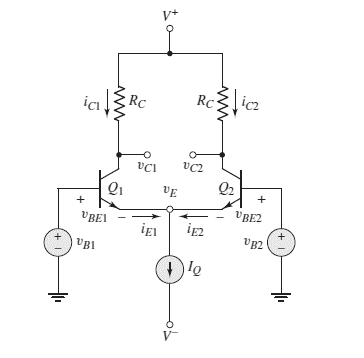
Calculation:
Voltage at emitter of each transistor
vE=v1−VBE(on)=−1−0.7 V
vE=−1.7 V
Assume transistors are matched. Then,
iE1=iE2=IQ2
Also assume the bias currents are negligible. Then,
iC1≅iE1=IQ2,iC2≅iE2=IQ2
Now
vC1=vC2=V+−IQ2RC=5−0.15×20 V
vC1=2 V, vC2=2 V
Then,
vCE1=vC1−vE=2−(−1.7)
vCE1=3.7 V
Similarly,
vCE2=vC2−vE=2−(−0.7)
vCE2=3.7 V
c.
The collector voltages, collector to emitter voltages and the emitter voltage for the given values of differential amplifier.
Answer to Problem 11.1EP
vE=0.3 V , vC1=2 V , vC2=2 V , vCE1=1.7 V , vCE2=1.7 V
Explanation of Solution
Given Information:
The given values are:
V+=5 V, V−=−5 V,IQ=0.3 mA,RC=20 kΩ,β=180,VBE(on)=0.7 V,VA=∞v1=v2=+1 V
The given circuit is shown below.
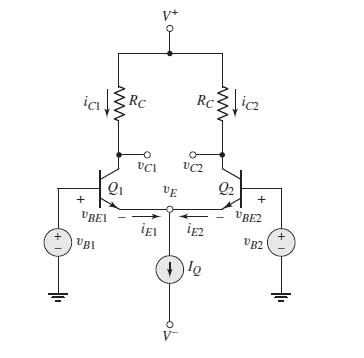
Calculation:
Voltage at emitter of each transistor
vE=v1−VBE(on)=1−0.7 V
vE=0.3 V
Assume transistors are matched. Then,
iE1=iE2=IQ2
Also assume the bias currents are negligible. Then,
iC1≅iE1=IQ2,iC2≅iE2=IQ2
Now
vC1=vC2=V+−IQ2RC=5−0.15×20 V
vC1=2 V, vC2=2 V
Then,
vCE1=vC1−vE=2−(0.3)
vCE1=1.7 V
Similarly,
vCE2=vC2−vE=2−(0.3)
vCE2=1.7 V
Want to see more full solutions like this?
Chapter 11 Solutions
Microelectronics: Circuit Analysis and Design
- 2. Using the approximate method, hand sketch the Bode plot for the following transfer functions. a) H(s) = 10 b) H(s) (s+1) c) H(s): = 1 = +1 100 1000 (s+1) 10(s+1) d) H(s) = (s+100) (180+1)arrow_forwardQ4: Write VHDL code to implement the finite-state machine described by the state Diagram in Fig. 1. Fig. 1arrow_forward1. Consider the following feedback system. Bode plot of G(s) is shown below. Phase (deg) Magnitude (dB) -50 -100 -150 -200 0 -90 -180 -270 101 System: sys Frequency (rad/s): 0.117 Magnitude (dB): -74 10° K G(s) Bode Diagram System: sys Frequency (rad/s): 36.8 Magnitude (dB): -99.7 System: sys Frequency (rad/s): 20 Magnitude (dB): -89.9 System: sys Frequency (rad/s): 20 Phase (deg): -143 System: sys Frequency (rad/s): 36.8 Phase (deg): -180 101 Frequency (rad/s) a) Determine the range of K for which the closed-loop system is stable. 102 10³ b) If we want the gain margin to be exactly 50 dB, what is value for K we should choose? c) If we want the phase margin to be exactly 37°, what is value of K we should choose? What will be the corresponding rise time (T) for step-input? d) If we want steady-state error of step input to be 0.6, what is value of K we should choose?arrow_forward
- : Write VHDL code to implement the finite-state machine/described by the state Diagram in Fig. 4. X=1 X=0 solo X=1 X=0 $1/1 X=0 X=1 X=1 52/2 $3/3 X=1 Fig. 4 X=1 X=1 56/6 $5/5 X=1 54/4 X=0 X-O X=O 5=0 57/7arrow_forwardQuestions: Q1: Verify that the average power generated equals the average power absorbed using the simulated values in Table 7-2. Q2: Verify that the reactive power generated equals the reactive power absorbed using the simulated values in Table 7-2. Q3: Why it is important to correct the power factor of a load? Q4: Find the ideal value of the capacitor theoretically that will result in unity power factor. Vs pp (V) VRIPP (V) VRLC PP (V) AT (μs) T (us) 8° pf Simulated 14 8.523 7.84 84.850 1000 29.88 0.866 Measured 14 8.523 7.854 82.94 1000 29.85 0.86733 Table 7-2 Power Calculations Pvs (mW) Qvs (mVAR) PRI (MW) Pay (mW) Qt (mVAR) Qc (mYAR) Simulated -12.93 -7.428 9.081 3.855 12.27 -4.84 Calculated -12.936 -7.434 9.083 3.856 12.32 -4.85 Part II: Power Factor Correction Table 7-3 Power Factor Correction AT (us) 0° pf Simulated 0 0 1 Measured 0 0 1arrow_forwardQuestions: Q1: Verify that the average power generated equals the average power absorbed using the simulated values in Table 7-2. Q2: Verify that the reactive power generated equals the reactive power absorbed using the simulated values in Table 7-2. Q3: Why it is important to correct the power factor of a load? Q4: Find the ideal value of the capacitor theoretically that will result in unity power factor. Vs pp (V) VRIPP (V) VRLC PP (V) AT (μs) T (us) 8° pf Simulated 14 8.523 7.84 84.850 1000 29.88 0.866 Measured 14 8.523 7.854 82.94 1000 29.85 0.86733 Table 7-2 Power Calculations Pvs (mW) Qvs (mVAR) PRI (MW) Pay (mW) Qt (mVAR) Qc (mYAR) Simulated -12.93 -7.428 9.081 3.855 12.27 -4.84 Calculated -12.936 -7.434 9.083 3.856 12.32 -4.85 Part II: Power Factor Correction Table 7-3 Power Factor Correction AT (us) 0° pf Simulated 0 0 1 Measured 0 0 1arrow_forward
- electric plants. Prepare the load schedulearrow_forwardelectric plants Draw the column diagram. Calculate the voltage drop. by hand writingarrow_forwardelectric plants. Draw the lighting, socket, telephone, TV, and doorbell installations on the given single-story project with an architectural plan by hand writingarrow_forward
- A circularly polarized wave, traveling in the +z-direction, is received by an elliptically polarized antenna whose reception characteristics near the main lobe are given approx- imately by E„ = [2â, + jâ‚]ƒ(r. 8, 4) Find the polarization loss factor PLF (dimensionless and in dB) when the incident wave is (a) right-hand (CW) An elliptically polarized wave traveling in the negative z-direction is received by a circularly polarized antenna. The vector describing the polarization of the incident wave is given by Ei= 2ax + jay.Find the polarization loss factor PLF (dimensionless and in dB) when the wave that would be transmitted by the antenna is (a) right-hand CParrow_forwardjX(1)=j0.2p.u. jXa(2)=j0.15p.u. jxa(0)=0.15 p.u. V₁=1/0°p.u. V₂=1/0° p.u. 1 jXr(1) = j0.15 p.11. jXT(2) = j0.15 p.u. jXr(0) = j0.15 p.u. V3=1/0° p.u. А V4=1/0° p.u. 2 jX1(1)=j0.12 p.u. 3 jX2(1)=j0.15 p.u. 4 jX1(2)=0.12 p.11. JX1(0)=0.3 p.u. jX/2(2)=j0.15 p.11. X2(0)=/0.25 p.1. Figure 1. Circuit for Q3 b).arrow_forwardcan you show me full workings for this problem. the solution is - v0 = 10i2 = 2.941 volts, i0 = i1 – i2 = (5/3)i2 = 490.2mA.arrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





