Fox and McDonald's Introduction to Fluid Mechanics
9th Edition
ISBN: 9781118912652
Author: Philip J. Pritchard, John W. Mitchell
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6, Problem 25P
Repeat Example 6.1, but with the somewhat more realistic assumption that the flow is similar to a free vortex (irrotational) profile, Vθ = c/r (where c is a constant), as shown in Fig. P6.25. In doing so, prove that the flow rate is given by Q=k√Δp, where k is
k=w ln(r2r1)√2r22r21ρ(r22−r21)
and w is the depth of the bend.
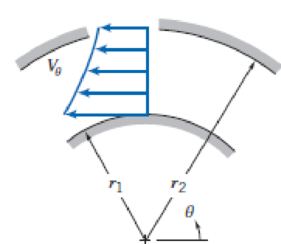
P6.25
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Thermodynamics: Mass and Energy Analysis Of Control Volumes
A 12-ft3 tank contains oxygen at 15 psia and 80◦F. A paddle wheel within the tank is rotated until thepressure inside rises to 20 psia. During the process 25 Btu of heat is lost to the surroundings. Determine thepaddle wheel work done. Neglect the energy stored in the paddle wheel.
Thermodynamics: Mass and Energy Analysis Of Control Volumes
A frictionless piston-cylinder device contains 4.5 kg of nitrogen at 110 kPa and 200 K. Nitrogen is nowcompressed slowly according to the relation PV1.5 = constant until it reaches a final temperature of 360 K.Calculate the work input during the process, in kJ.
Thermodynamics: Mass and Energy Analysis Of Control Volumes
An insulated piston-cylinder device contains 4 L of saturated liquid water at a constant pressure of 200 kPa.Water is stirred by a paddle wheel while a current of 8 A flows for 50 min through a resistor placed in thewater. If one-half of the liquid is evaporated during this constant-pressure process and the paddle-wheelwork amounts to 300 kJ, determine the voltage of the source. Also, show the process on a P–v diagram withrespect to the saturation lines.
Chapter 6 Solutions
Fox and McDonald's Introduction to Fluid Mechanics
Ch. 6 - An incompressible frictionless flow field is given...Ch. 6 - A velocity field in a fluid with density of 1000...Ch. 6 - The x component of velocity in an incompressible...Ch. 6 - Consider the flow field with the velocity given by...Ch. 6 - Consider the flow field with the velocity given by...Ch. 6 - The velocity field for a plane source located...Ch. 6 - In a two-dimensional frictionless, incompressible...Ch. 6 - Consider a two-dimensional incompressible flow...Ch. 6 - An incompressible liquid with a density of 900...Ch. 6 - Consider a flow of water in pipe. What is the...
Ch. 6 - The velocity field for a plane vortex sink is...Ch. 6 - An incompressible liquid with negligible viscosity...Ch. 6 - Consider water flowing in a circular section of a...Ch. 6 - Consider a tornado as air moving in a circular...Ch. 6 - A nozzle for an incompressible, inviscid fluid of...Ch. 6 - A diffuser for an incompressible, inviscid fluid...Ch. 6 - A liquid layer separates two plane surfaces as...Ch. 6 - Consider Problem 6.15 with the nozzle directed...Ch. 6 - Consider Problem 6.16 with the diffuser directed...Ch. 6 - A rectangular computer chip floats on a thin layer...Ch. 6 - Heavy weights can be moved with relative ease on...Ch. 6 - The y component of velocity in a two-dimensional...Ch. 6 - The velocity field for a plane doublet is given in...Ch. 6 - Tomodel the velocity distribution in the curved...Ch. 6 - Repeat Example 6.1, but with the somewhat more...Ch. 6 - Using the analyses of Example 6.1 and Problem...Ch. 6 - Water flows at a speed of 25 ft/s. Calculate the...Ch. 6 - Plot the speed of air versus the dynamic pressure...Ch. 6 - Water flows in a pipeline. At a point in the line...Ch. 6 - In a pipe 0.3 m in diameter, 0.3 m3/s of water are...Ch. 6 - A jet of air from a nozzle is blown at right...Ch. 6 - The inlet contraction and test section of a...Ch. 6 - Maintenance work on high-pressure hydraulic...Ch. 6 - An open-circuit wind tunnel draws in air from the...Ch. 6 - Water is flowing. Calculate H(m) and p(kPa). P6.36Ch. 6 - If each gauge shows the same reading for a flow...Ch. 6 - Derive a relation between A1 and A2 so that for a...Ch. 6 - Water flows steadily up the vertical 1...Ch. 6 - Your car runs out of gas unexpectedly and you...Ch. 6 - A tank at a pressure of 50 kPa gage gets a pinhole...Ch. 6 - The water flow rate through the siphon is 5 L/s,...Ch. 6 - Water flows from a very large tank through a 5 cm...Ch. 6 - Consider frictionless, incompressible flow of air...Ch. 6 - A closed tank contains water with air above it....Ch. 6 - Water jets upward through a 3-in.-diameter nozzle...Ch. 6 - Calculate the rate of flow through this pipeline...Ch. 6 - A mercury barometer is carried in a car on a day...Ch. 6 - A racing car travels at 235 mph along a...Ch. 6 - The velocity field for a plane source at a...Ch. 6 - A smoothly contoured nozzle, with outlet diameter...Ch. 6 - Water flows steadily through a 3.25-in.-diameter...Ch. 6 - A flow nozzle is a device for measuring the flow...Ch. 6 - The head of water on a 50 mm diameter smooth...Ch. 6 - Water flows from one reservoir in a 200-mm pipe,...Ch. 6 - Barometric pressure is 14.0 psia. What is the...Ch. 6 - A spray system is shown in the diagram. Water is...Ch. 6 - Water flows out of a kitchen faucet of...Ch. 6 - A horizontal axisymmetric jet of air with...Ch. 6 - The water level in a large tank is maintained at...Ch. 6 - Many recreation facilities use inflatable bubble...Ch. 6 - Water flows at low speed through a circular tube...Ch. 6 - Describe the pressure distribution on the exterior...Ch. 6 - An aspirator provides suction by using a stream of...Ch. 6 - Carefully sketch the energy grade lines (EGL) and...Ch. 6 - Carefully sketch the energy grade lines (EGL) and...Ch. 6 - Water is being pumped from the lower reservoir...Ch. 6 - The turbine extracts power from the water flowing...Ch. 6 - Consider a two-dimensional fluid flow: u = ax + by...Ch. 6 - The velocity field for a two-dimensional flow is...Ch. 6 - A flow field is characterized by the stream...Ch. 6 - The flow field for a plane source at a distance h...Ch. 6 - The stream function of a flow field is = Ax2y ...Ch. 6 - A flow field is characterized by the stream...Ch. 6 - A flow field is characterized by the stream...Ch. 6 - The stream function of a flow field is = Ax3 ...Ch. 6 - A flow field is represented by the stream function...Ch. 6 - Consider the flow field represented by the...Ch. 6 - Show by expanding and collecting real and...Ch. 6 - Consider the flow field represented by the...Ch. 6 - An incompressible flow field is characterized by...Ch. 6 - Consider an air flow over a flat wall with an...Ch. 6 - A source with a strength of q = 3 m2/s and a sink...Ch. 6 - The velocity distribution in a two-dimensional,...Ch. 6 - Consider the flow past a circular cylinder, of...Ch. 6 - The flow in a corner with an angle can be...Ch. 6 - Consider the two-dimensional flow against a flat...Ch. 6 - A source and a sink with strengths of equal...Ch. 6 - A flow field is formed by combining a uniform flow...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Thermodynamics: Mass and Energy Analysis Of Control Volumes The state of liquid water is changed from 55 psia and 45◦F to 2000 psia and 120◦F. Determine the change inthe internal energy and enthalpy of water on the basis of the (a) compressed liquid tables, (b) incompressiblesubstance approximation and property tables, and (c) specific-heat model.arrow_forwardThermodynamics: Mass and Energy Analysis Of Control Volumes What is the change in enthalpy, in kJ/kg, of oxygen as its temperature changes from 150 to 250◦C? Is thereany difference if the temperature change were from −50 to 100◦C? Does the pressure at the beginning andend of this process have any effect on the enthalpy change?arrow_forwardThermodynamics: Mass and Energy Analysis Of Control Volumes A 50-L electrical radiator containing heating oil is placed in a 50-m3 room. Both the room and the oil in theradiator are initially at 5◦C. The radiator with a rating of 3 kW is now turned on. At the same time, heatis lost from the room at an average rate of 0.3 kJ/s. After some time, the average temperature is measuredto be 20◦C for the air in the room, and 60◦C for the oil in the radiator. Taking the density and the specificheat of the oil to be 950 kg/m3 and 2.2 kJ/(kg◦C), respectively, determine how long the heater is kept on.Assume the room is well-sealed so that there are no air leaks.arrow_forward
- Problem 3 For the beam and loading shown, consider section n-n and determine (a) the largest shearing stress in that section, (b) the shearing stress at point a. 1ft 15 kips 20 kips 15 kips AITT in 1 0.6 in. -10 in. 1 in. 0.375 in.- 2 ft 2ft 2 ft 2ft 10 in. 1 0.6 in.arrow_forwardpractice problems want detailed break downarrow_forward6.105. Determine force P on the cable if the spring is compressed 0.025 m when the mechanism is in the position shown. The spring has a stiffness of k = 6 kN/m. E P 150 mm D T 30° 200 mm 200 mm 200 mm B 800 mmarrow_forward
- 6.71. Determine the reactions at the supports A, C, and E of the compound beam. 3 kN/m 12 kN A B CD E -3 m 4 m 6 m 3 m 2 marrow_forwardA countershaft carrying two V-belt pullets is shown in the figure. Pulley A receives power from a motor through a belt with the belt tensions shown. The power is transmitted through the shaft and delivered to the belt on pulley B. Assume the belt tension on the loose side (T1) at B is 30% of the tension on the tight side (T2). (a) Determine the tension (i.e., T₂ and T₁) in the belt on pulley B, assuming the shaft is running at a constant speed. (b) Find the magnitudes of the bearing reaction forces, assuming the bearings act as simple supports. (c) Draw shear-force and bending moment diagrams for the shaft (in XZ and XY plane if needed). (d) Calculate the maximum moments at points A and B respectively and find the point of maximum bending moment (A or B). (e) Find maximum stresses (tensile, compressive, and shear stresses) at the identified point of maximum moment (hint: principal and max shear stresses) 8 dia. 9 400lbf 50lbf 45° 1.5 dia. T₂ B Units in inches T₁ 10 dia.arrow_forwardThe cantilevered bar in the figure is made from a ductile material and is statically loaded with F,, = 200 lbf and Fx = F₂ = 0. Analyze the stress situation in rod AB by obtaining the following information. Note that the stress concentration factors are neglected in the following questions (Kt and Kts=1). (a) Determine the precise location of the critical stress element. (b) Sketch the critical stress element and determine magnitudes and direction for all stresses acting on it. (Transverse shear may only be neglected if you can justify this decision.) (c) For the critical stress element, determine the principal stresses and maximum shear stress. 6 in 1-in dia. B +1- in in 2 in 5 inarrow_forward
- A laminated thick-walled hydraulic cylinder was fabricated by shrink-fitting jacket having an outside diameter of 300mm onto a SS 304 steel tube having an inside diameter of 100mm and an outside diameter of 200mm as shown in the figure. The interference (8) was 0.15mm. When the Young's modulus for both SS304 and 1020 steel is the same as 200GPa, and the Poisson's ratio is also the same as 0.3 for both materials, find the followings. Initially 100 mm Initially 200 mm Initially 300 mm SS 304 1020 steel (a) P; (interfacial contact stress) (b) The maximum stresses (σ, and σ+) in the laminated steel cylinder resulting from the shrink fit.arrow_forwardAuto Controls Design a proportional derivitivecontroller for a plant orsystemthat satisfies the following specifications : 1. is steady-state error is less than 2 % for a ramp input. 2.) Damping ratio (zeta) is greater than 0.7have determined the 3. Once youvalue of kp and kd, then plotthe response of the compensated(with controller) and uncompensated( without the controller, only the plantsystem using MATLAB.arrow_forwardAuto Controls (a) Refer to the above figure .What kind of controller is it ? (b) simplify the block diagramto derive the closed loop transfer function of the system. (C) What are the assumptions thatare needed to make to findthe controller gain ? What arethe value of Kp , Ti and Td ?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
8.01x - Lect 27 - Fluid Mechanics, Hydrostatics, Pascal's Principle, Atmosph. Pressure; Author: Lectures by Walter Lewin. They will make you ♥ Physics.;https://www.youtube.com/watch?v=O_HQklhIlwQ;License: Standard YouTube License, CC-BY
Dynamics of Fluid Flow - Introduction; Author: Tutorials Point (India) Ltd.;https://www.youtube.com/watch?v=djx9jlkYAt4;License: Standard Youtube License