Chapter 8.3, Problem 19IP

a.

To determine

The expression to represent the amount of money saved after w weeks.

Answer to Problem 19IP

  $7+4x+\left(-4\right)+\left(-2x\right)+3=6+2x$

Explanation of Solution

Given:

She is saving money to buy an MP3 player that costs $212. She already saved $47 and plans to save an additional $15 per week.

Calculation:

In order to write an expression to represent the amount of money saved after w weeks, observe that she already have save $47, so it is the fixed amount and she plans to save an additional $15 every week, so an expression to represent the situation could be

  $\begin{array}{c}\text{Amount of saving}=\text{saved money + 15}\left(\text{number of weeks}\right)\\ A=47+15w\end{array}$

Thus, the expression to represent the amount of money saved after w weeks is $A=47+15w$ .

So, the table can be filled using this expression as

Number of weeks	Amount of saving ($)
1	$47+15\left(1\right)=62$
2	$47+15\left(2\right)=77$
3	$47+15\left(3\right)=92$
4	$47+15\left(4\right)=107$

b.

To determine

The line graph of the data in the table.

Explanation of Solution

Given:

She is saving money to buy an MP3 player that costs $212. She already saved $47 and plans to save an additional $15 per week.

Calculation:

The plot of the data points from the table is shown below,

  

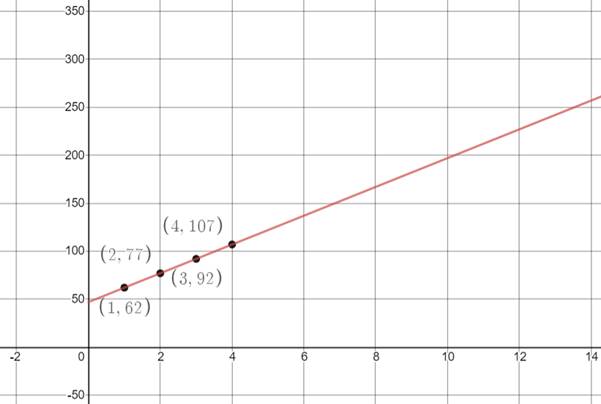
From the graph it is clear that she will have enough money for the MP3 player after 11^th week.

c.

To determine

The number of weeks it will take her to save the money.

Answer to Problem 19IP

  $7+4x+\left(-4\right)+\left(-2x\right)+3=6+2x$

Explanation of Solution

Given:

She is saving money to buy an MP3 player that costs $212. She already saved $47 and plans to save an additional $15 per week.

Calculation:

In order to write an expression to represent the amount of money saved after w weeks, observe that she already have save $47, so it is the fixed amount and she plans to save an additional $15 every week, so an expression to represent the situation could be

  $\begin{array}{c}\text{Amount of saving}=\text{saved money + 15}\left(\text{number of weeks}\right)\\ A=47+15w\end{array}$

Since the cost of the MP3 player is $212, so substitute this value of A in above equation and solve for w as shown below,

  $\begin{array}{c}212=47+15w\\ 15w=212-47\\ 15w=165\\ w=\frac{165}{15}\\ w=11\end{array}$

So, it will take her 11 weeks to save the money to buy MP3.

d.

To determine

To compare the methods for finding the solution used in part (b) and (c).

Explanation of Solution

Given:

She is saving money to buy an MP3 player that costs $212. She already saved $47 and plans to save an additional $15 per week.

Calculation:

Using the graph, once can estimate the time when she can have enough money to buy the MP3, while using the equation, one can find the exact time when she will have the required amount of money.