
Concept explainers
(a)
An equation that represents the distance d the butterfly will travel in t days
The equation is
Given:
The North American Monarch butterfly migrates up to 3000 miles to California and butterfly travels on average 52.5 miles per day
Concept Used:
Rules of Addition/ Subtraction:
- Two numbers with similar sign always get added and the resulting number will carry the similar sign.
- Two numbers with opposite signs always get subtracted and the resulting number will carry the sign of larger number.
Rules of Multiplication/ Division:
- The product/quotient of two similar sign numbers is always positive.
- The product/quotient of two numbers with opposite signs is always negative.
Calculation:
In order to find the equation the distance d the butterfly will travel in t days with the average speed of 52.5 miles is below:
Thus, the equation is
(b)
Complete the table
The table is below
| Time (days) | 1 | 2 | 3 | 4 | 5 | 6 |
| Distance (miles) | 52.5 | 105 | 157.5 | 210 | 262.5 | 315 |
Given:

Concept Used:
Rules of Addition/ Subtraction:
- Two numbers with similar sign always get added and the resulting number will carry the similar sign.
- Two numbers with opposite signs always get subtracted and the resulting number will carry the sign of larger number.
Rules of Multiplication/ Division:
- The product/quotient of two similar sign numbers is always positive.
- The product/quotient of two numbers with opposite signs is always negative.
Calculation:
In order to complete the table by using equation
| Time (days) | 1 | 2 | 3 | 4 | 5 | 6 |
| Distance (miles) |
Thus, the table is below
| Time (days) | 1 | 2 | 3 | 4 | 5 | 6 |
| Distance (miles) | 52.5 | 105 | 157.5 | 210 | 262.5 | 315 |
(c)
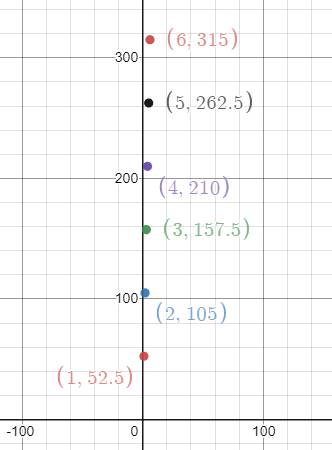
The graph of points in the table
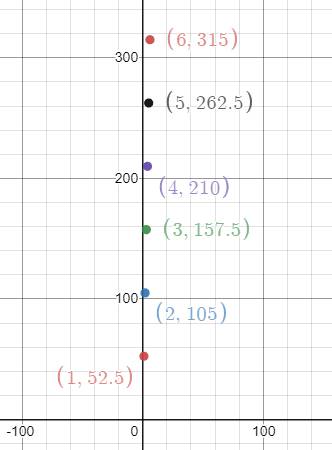
Given:
The table is below
| Time (days) | 1 | 2 | 3 | 4 | 5 | 6 |
| Distance (miles) | 52.5 | 105 | 157.5 | 210 | 262.5 | 315 |
Concept Used:
In rectangular coordinate system any point be in the form of
In Quadrant I, both the coordinates of ordered pair are positive, that is,
In Quadrant II, first number is negative and second is positive, that is,
In Quadrant III, both the coordinates of ordered pair are negative, that is,
In Quadrant IV, first point is positive and second is negative, that is,
Explanation: In order to plot the point
To plot the graph of the point
To plot the graph of the point
To plot the graph of the point
To plot the graph of the point
To plot the graph of the point
To plot the graph of the point
To plot the graph of the point
The graph of the point is shown below:
(d)
The number of days it will take the butterfly to travel 475 days
The time is
Given:
Butterfly travels 475 miles
Concept Used:
Rules of Addition/ Subtraction:
- Two numbers with similar sign always get added and the resulting number will carry the similar sign.
- Two numbers with opposite signs always get subtracted and the resulting number will carry the sign of larger number.
Rules of Multiplication/ Division:
- The product/quotient of two similar sign numbers is always positive.
- The product/quotient of two numbers with opposite signs is always negative.
Calculation:
In order to find the time is below:
Thus, the time is
(e)
How many days will it take the butterfly to travel 2100 miles
The days that the butterfly to travel 2100 miles is
Given:
Concept Used:
Rules of Addition/ Subtraction:
- Two numbers with similar sign always get added and the resulting number will carry the similar sign.
- Two numbers with opposite signs always get subtracted and the resulting number will carry the sign of larger number.
Rules of Multiplication/ Division:
- The product/quotient of two similar sign numbers is always positive.
- The product/quotient of two numbers with opposite signs is always negative.
Calculation:
In order to find the days is below:
Thus, the days that the butterfly to travel 2100 miles is
Chapter 8 Solutions
Glencoe Math Accelerated, Student Edition
Additional Math Textbook Solutions
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Pre-Algebra Student Edition
A First Course in Probability (10th Edition)
Elementary Statistics (13th Edition)
University Calculus: Early Transcendentals (4th Edition)
- After a great deal of experimentation, two college senior physics majors determined that when a bottle of French champagne is shaken several times, held upright, and uncorked, its cork travels according to the function below, where s is its height (in feet) above the ground t seconds after being released. s(t)=-16t² + 30t+3 a. How high will it go? b. How long is it in the air?arrow_forward+6x²+135x+1) (0≤x≤10). a) Find the number of units The total profit P(x) (in thousands of dollars) from a sale of x thousand units of a new product is given by P(x) = In (-x²+6x² + 135x+ that should be sold in order to maximize the total profit. b) What is the maximum profit?arrow_forwardThe fox population in a certain region has an annual growth rate of 8 percent per year. It is estimated that the population in the year 2000 was 22600. (a) Find a function that models the population t years after 2000 (t = 0 for 2000). Your answer is P(t) = (b) Use the function from part (a) to estimate the fox population in the year 2008. Your answer is (the answer should be an integer)arrow_forward
- rarrow_forwardThe solutions are 1 where x1 x2- ● Question 11 Solve: x 54 Give your answer as an interval. Question 12arrow_forwardA population of deer in Pierce County currently has 1875 deer, but due to urban development, the population is decreasing at a rate of 1.1% a year. a) Assuming this growth rate continues, find the formula for a function f(t) describing this population. b) In how many years will the population reach 1300? Do the problems on your own paper, show all your work, and submit your scanned work below. Choose File No file chosenarrow_forward
- Question 3 Rewrite 4 = log₂(16) in exponential form. Question 4 症 If log, (6x+3)= 4, then rarrow_forwardQuestion 6 Find the solution of the exponential equation 2t 100(1.07) 2 = 500,000 in terms of logarithms, or correct to four decimal places. t=arrow_forwardQuestion 6 Find the solution of the exponential equation 100(1.07)² = 500, 000 in terms of logarithms, or correct to four decimal places. t = Question 7 Solve the equation.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





