The Practice of Statistics for AP - 4th Edition
4th Edition
ISBN: 9781429245593
Author: Starnes, Daren S., Yates, Daniel S., Moore, David S.
Publisher: Macmillan Higher Education
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 2.2, Problem 63E
(a)
To determine
To describe: the shape, center, and spread of the distribution of shark lengths
(a)
Expert Solution
Answer to Problem 63E
Shape: symmetric and roughly bell-shaped.
Center:
Spread: standard deviation is 2.5499
Explanation of Solution
Given:
| 18.7 | 12.3 | 18.6 | 16.4 | 15.7 | 18.3 | 14.6 | 15.8 | 14.9 | 17.6 | 12.1 |
| 16.4 | 16.7 | 17.8 | 16.2 | 12.6 | 17.8 | 13.8 | 12.2 | 15.2 | 14.7 | 12.4 |
| 13.2 | 15.8 | 14.3 | 16.6 | 9.4 | 18.2 | 13.2 | 13.6 | 15.3 | 16.1 | 13.5 |
| 19.1 | 16.2 | 22.8 | 16.8 | 13.6 | 131 | 15.7 | 19.7 | 18.7 | 13.2 | 16.8 |
Lengths of sharks are in feet of 44
Calculation:
| Variable | N | Mean | St.Dev. | Min | Q1 | M | Q3 | Max |
| Shark length | 44 | 15.586 | 2.550 | 9.40 | 13.525 | 15.75 | 17.40 | 22.80 |
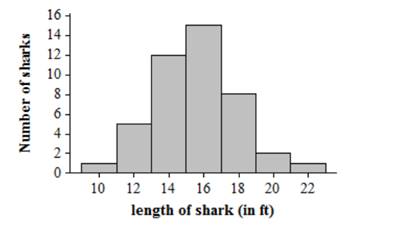
Shark lengths are roughly symmetric with a peak at 16 and vary from minimum value of 9.40 feet to maximum value 22.8 feet.
Shape: symmetric and roughly bell-shaped.
Center: Mean is 15.5884 and median is 15.75
Spread: standard deviation is 2.5499
Conclusion:
Shape: symmetric and roughly bell-shaped.
Center: Mean is 15.5884 and median is 15.75
Spread: standard deviation is 2.5499
(b)
To determine
To describe: the percent of observations that fall within one, two, and three standard deviations of the mean.
(b)
Expert Solution
Answer to Problem 63E
One standard deviations = 68.2%
Two standard deviations = 95.5%
Three standard deviations = 100%
Explanation of Solution
Calculation:
From the above output,
Mean, ˉx=15.586
Sample standard deviation, s=2.550
ˉx−s=13.036ˉx+s=18.136
Percent of interval
(68.26%) 68.2%
ˉx−2s=10.487ˉx+2s=20.686
Percent of interval
(95.44%) 95.5%
ˉx−3s=7.937ˉx+3s=23.236
Percent of interval
(99.73%) 100.0%
According to the 68-95-99.7 rule, approximately 68.2% of the data values fall within one standard deviation. 95.5% of the data values fall within two standard deviations, and 100% of the data values fall within three standard deviations of the mean.
Conclusion:
Therefore,
One standard deviations = 68.2%
Two standard deviations = 95.5%
Threestandard deviations = 100%
(c)
To determine
To construct: a Normal
(c)
Expert Solution
Answer to Problem 63E
The pattern in the Normal probability plot is fairly linear and it is roughly
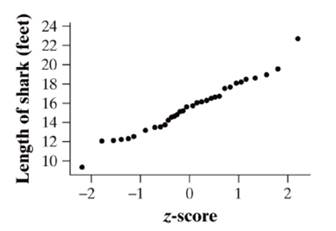
Explanation of Solution
Calculation:
A Normal probability plot from Minitab is shown below:
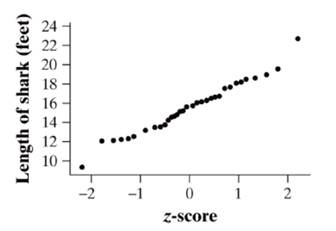
The plot is fairly linear except from one small shark and one large shark lengths, indicating that the Normal distribution is appropriate.
Conclusion:
Therefore, a Normal probability plot is plotted. The pattern in the Normal probability plot is fairly linear and it is roughly normally distributed.
(c)
To determine
To explain:whether the data are approximately Normal
(c)
Expert Solution
Answer to Problem 63E
The data are approximately Normal
Explanation of Solution
Calculation:
Results from the parts (a), (b), and (c) indicates that shark lengths are approximately normal.
Approximately normal, because the normal probability plot was roughlynormal and the histogram were roughly bell-shaped.
Conclusion:
Therefore, the data are approximately Normal
Chapter 2 Solutions
The Practice of Statistics for AP - 4th Edition
Ch. 2.1 - Prob. 1.1CYUCh. 2.1 - Prob. 1.2CYUCh. 2.1 - Prob. 1.3CYUCh. 2.1 - Prob. 1.4CYUCh. 2.1 - Prob. 2.1CYUCh. 2.1 - Prob. 2.2CYUCh. 2.1 - Prob. 2.3CYUCh. 2.1 - Prob. 3.1CYUCh. 2.1 - Prob. 3.2CYUCh. 2.1 - Prob. 3.3CYU
Ch. 2.1 - Prob. 4.1CYUCh. 2.1 - Prob. 4.2CYUCh. 2.1 - Prob. 4.3CYUCh. 2.1 - Prob. 1ECh. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10ECh. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.2 - Prob. 1.1CYUCh. 2.2 - Prob. 1.2CYUCh. 2.2 - Prob. 1.3CYUCh. 2.2 - Prob. 2.1CYUCh. 2.2 - Prob. 2.2CYUCh. 2.2 - Prob. 2.3CYUCh. 2.2 - Prob. 2.4CYUCh. 2.2 - Prob. 2.5CYUCh. 2.2 - Prob. 3.1CYUCh. 2.2 - Prob. 3.2CYUCh. 2.2 - Prob. 3.3CYUCh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - Prob. 51ECh. 2.2 - Prob. 52ECh. 2.2 - Prob. 53ECh. 2.2 - Prob. 54ECh. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - Prob. 57ECh. 2.2 - Prob. 58ECh. 2.2 - Prob. 59ECh. 2.2 - Prob. 60ECh. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - Prob. 63ECh. 2.2 - Prob. 64ECh. 2.2 - Prob. 65ECh. 2.2 - Prob. 66ECh. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - Prob. 69ECh. 2.2 - Prob. 70ECh. 2.2 - Prob. 71ECh. 2.2 - Prob. 72ECh. 2.2 - Prob. 73ECh. 2.2 - Prob. 74ECh. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2 - Prob. 1CRECh. 2 - Prob. 2CRECh. 2 - Prob. 3CRECh. 2 - Prob. 4CRECh. 2 - Prob. 5CRECh. 2 - Prob. 6CRECh. 2 - Prob. 7CRECh. 2 - Prob. 8CRECh. 2 - Prob. 9CRECh. 2 - Prob. 10CRECh. 2 - Prob. 11CRECh. 2 - Prob. 12CRECh. 2 - Prob. 1PTCh. 2 - Prob. 2PTCh. 2 - Prob. 3PTCh. 2 - Prob. 4PTCh. 2 - Prob. 5PTCh. 2 - Prob. 6PTCh. 2 - Prob. 7PTCh. 2 - Prob. 8PTCh. 2 - Prob. 9PTCh. 2 - Prob. 10PTCh. 2 - Prob. 11PTCh. 2 - Prob. 12PTCh. 2 - Prob. 13PT
Additional Math Textbook Solutions
Find more solutions based on key concepts
Find the line integral of f(x, y, z) = x + y + z over the straight-line segment from (1, 2, 3) to (0, −1, 1).
University Calculus: Early Transcendentals (4th Edition)
Find how many SDs above the mean price would be predicted to cost.
Intro Stats, Books a la Carte Edition (5th Edition)
Confidence Intervals. In Exercises 9–24, construct the confidence interval estimate of the mean.
12. Atkins Wei...
Elementary Statistics (13th Edition)
Disks/washers about the y-axis Let R be the region bounded by the following curves. Use the disk or washer meth...
Calculus: Early Transcendentals (2nd Edition)
In Exercises 13–16, find the margin of error for the values of c, ?, and n.
13. c = 0.95, ? = 5.2, n = 30
Elementary Statistics: Picturing the World (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Could you please answer this question using excel. For 1a) I got 84.75 and for part 1b) I got 85.33 and was wondering if you could check if my answers were correct. Thanksarrow_forwardWhat is one sample T-test? Give an example of business application of this test? What is Two-Sample T-Test. Give an example of business application of this test? .What is paired T-test. Give an example of business application of this test? What is one way ANOVA test. Give an example of business application of this test? 1. One Sample T-Test: Determine whether the average satisfaction rating of customers for a product is significantly different from a hypothetical mean of 75. (Hints: The null can be about maintaining status-quo or no difference; If your alternative hypothesis is non-directional (e.g., μ≠75), you should use the two-tailed p-value from excel file to make a decision about rejecting or not rejecting null. If alternative is directional (e.g., μ < 75), you should use the lower-tailed p-value. For alternative hypothesis μ > 75, you should use the upper-tailed p-value.) H0 = H1= Conclusion: The p value from one sample t-test is _______. Since the two-tailed p-value…arrow_forwardUsing the accompanying Accounting Professionals data to answer the following questions. a. Find and interpret a 90% confidence interval for the mean years of service. b. Find and interpret a 90% confidence interval for the proportion of employees who have a graduate degree. view the Accounting Professionals data. Employee Years of Service Graduate Degree?1 26 Y2 8 N3 10 N4 6 N5 23 N6 5 N7 8 Y8 5 N9 26 N10 14 Y11 10 N12 8 Y13 7 Y14 27 N15 16 Y16 17 N17 21 N18 9 Y19 9 N20 9 N Question content area bottom Part 1 a. A 90% confidence interval for the mean years of service is (Use ascending order. Round to two decimal places as needed.)arrow_forward
- If, based on a sample size of 900,a political candidate finds that 509people would vote for him in a two-person race, what is the 95%confidence interval for his expected proportion of the vote? Would he be confident of winning based on this poll? Question content area bottom Part 1 A 9595% confidence interval for his expected proportion of the vote is (Use ascending order. Round to four decimal places as needed.)arrow_forwardQuestions An insurance company's cumulative incurred claims for the last 5 accident years are given in the following table: Development Year Accident Year 0 2018 1 2 3 4 245 267 274 289 292 2019 255 276 288 294 2020 265 283 292 2021 263 278 2022 271 It can be assumed that claims are fully run off after 4 years. The premiums received for each year are: Accident Year Premium 2018 306 2019 312 2020 318 2021 326 2022 330 You do not need to make any allowance for inflation. 1. (a) Calculate the reserve at the end of 2022 using the basic chain ladder method. (b) Calculate the reserve at the end of 2022 using the Bornhuetter-Ferguson method. 2. Comment on the differences in the reserves produced by the methods in Part 1.arrow_forwardA population that is uniformly distributed between a=0and b=10 is given in sample sizes 50( ), 100( ), 250( ), and 500( ). Find the sample mean and the sample standard deviations for the given data. Compare your results to the average of means for a sample of size 10, and use the empirical rules to analyze the sampling error. For each sample, also find the standard error of the mean using formula given below. Standard Error of the Mean =sigma/Root Complete the following table with the results from the sampling experiment. (Round to four decimal places as needed.) Sample Size Average of 8 Sample Means Standard Deviation of 8 Sample Means Standard Error 50 100 250 500arrow_forward
- A survey of 250250 young professionals found that two dash thirdstwo-thirds of them use their cell phones primarily for e-mail. Can you conclude statistically that the population proportion who use cell phones primarily for e-mail is less than 0.720.72? Use a 95% confidence interval. Question content area bottom Part 1 The 95% confidence interval is left bracket nothing comma nothing right bracket0.60820.6082, 0.72510.7251. As 0.720.72 is within the limits of the confidence interval, we cannot conclude that the population proportion is less than 0.720.72. (Use ascending order. Round to four decimal places as needed.)arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forwardA survey of 250 young professionals found that two-thirds of them use their cell phones primarily for e-mail. Can you conclude statistically that the population proportion who use cell phones primarily for e-mail is less than 0.72? Use a 95% confidence interval. Question content area bottom Part 1 The 95% confidence interval is [ ], [ ] As 0.72 is ▼ above the upper limit within the limits below the lower limit of the confidence interval, we ▼ can cannot conclude that the population proportion is less than 0.72. (Use ascending order. Round to four decimal places as needed.)arrow_forward
- I need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
MATLAB: An Introduction with ApplicationsStatisticsISBN:9781119256830Author:Amos GilatPublisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...StatisticsISBN:9781305251809Author:Jay L. DevorePublisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...StatisticsISBN:9781305504912Author:Frederick J Gravetter, Larry B. WallnauPublisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...StatisticsISBN:9780134683416Author:Ron Larson, Betsy FarberPublisher:PEARSON
The Basic Practice of StatisticsStatisticsISBN:9781319042578Author:David S. Moore, William I. Notz, Michael A. FlignerPublisher:W. H. Freeman
Introduction to the Practice of StatisticsStatisticsISBN:9781319013387Author:David S. Moore, George P. McCabe, Bruce A. CraigPublisher:W. H. Freeman
MATLAB: An Introduction with Applications
Statistics
ISBN:9781119256830
Author:Amos Gilat
Publisher:John Wiley & Sons Inc
Probability and Statistics for Engineering and th...
Statistics
ISBN:9781305251809
Author:Jay L. Devore
Publisher:Cengage Learning
Statistics for The Behavioral Sciences (MindTap C...
Statistics
ISBN:9781305504912
Author:Frederick J Gravetter, Larry B. Wallnau
Publisher:Cengage Learning
Elementary Statistics: Picturing the World (7th E...
Statistics
ISBN:9780134683416
Author:Ron Larson, Betsy Farber
Publisher:PEARSON
The Basic Practice of Statistics
Statistics
ISBN:9781319042578
Author:David S. Moore, William I. Notz, Michael A. Fligner
Publisher:W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:9781319013387
Author:David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:W. H. Freeman
Statistics 4.1 Point Estimators; Author: Dr. Jack L. Jackson II;https://www.youtube.com/watch?v=2MrI0J8XCEE;License: Standard YouTube License, CC-BY
Statistics 101: Point Estimators; Author: Brandon Foltz;https://www.youtube.com/watch?v=4v41z3HwLaM;License: Standard YouTube License, CC-BY
Central limit theorem; Author: 365 Data Science;https://www.youtube.com/watch?v=b5xQmk9veZ4;License: Standard YouTube License, CC-BY
Point Estimate Definition & Example; Author: Prof. Essa;https://www.youtube.com/watch?v=OTVwtvQmSn0;License: Standard Youtube License
Point Estimation; Author: Vamsidhar Ambatipudi;https://www.youtube.com/watch?v=flqhlM2bZWc;License: Standard Youtube License