Concept explainers
Videos
a.
To calculate: The quartile points of the data.
a.
Answer to Problem 23E
The quartile points are Q1=424,Q2=538, and Q3=707.5
Explanation of Solution
Given information:
The data is on the college tution and fees.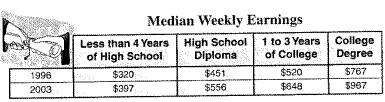 
Formula used:
If each group has the median, the data is divided into four groups. Each group is called quartile.
Median for even terms = (n2)thterm+(n2+1)thterm2
Median for odd terms = (n+12)thterm
Calculation:
Consider the data in ascending order ,
{$320,$397,$451,$520,$556,$648,$767,$967}.
So, n=8 .
There is even number of data.
The median of even number of data is −
=(82)thterm+(82+1)thterm2=(4)thterm+(5)thterm2=520+5562=10762=538
Therefore , the data is divided into two parts.
Lower half - $320,$397,$451,$520 and Upper half - $556,$648,$767,$967.
Median of lower half is −
=(42)thterm+(42+1)thterm2=(2)ndterm+(3)rdterm2=397+4512=8482=424
Median of upper half is −
=(42)thterm+(42+1)thterm2=(2)ndterm+(3)rdterm2=648+7672=14152=707.5
The quartile points are :-
Q1=424Q2=538Q3=707.5
Hence, the quartile points are Q1=424,Q2=538, and Q3=707.5
b.
To calculate: The interquartile range .
b.
Answer to Problem 23E
The interquartile range is 283.5.
Explanation of Solution
Given information:
The data is on the college tution and fees.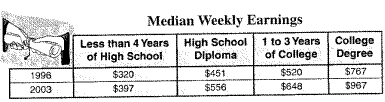 
Formula used:
The difference between the first quartile point and third quartile point is called the inter- quartile range.
Calculation:
Consider the data in ascending order ,
{$320,$397,$451,$520,$556,$648,$767,$967}.
So, n=8 .
There is even number of data.
The median of even number of data is 538.
The quartile points are :-
Q1=424Q2=538Q3=707.5
The inter- quartile range is Q3−Q1.
=707.5−424=283.5.
Hence, the interquartile range is 283.5.
c.
To show: whether there is any outliers.
c.
Answer to Problem 23E
No outliers.
Explanation of Solution
Given information:
The data is on the college tution and fees.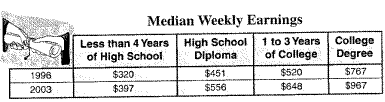 
Formula used:
Outliers are extreme values that are more than 1.5 times the interquartile range beyond the upper or lower quartiles .
Calculation:
Consider the data in ascending order ,
{$320,$397,$451,$520,$556,$648,$767,$967}.
There is even number of data.
The median of even number of data is 538.
The quartile points are :-
Q1=424Q2=538Q3=707.5
The inter- quartile range is 283.5.
For outlier
Q1−1.5(283.5)=424−425.25=−1.25Q3+1.5(283.5)=707.5+425.25=1132.75
The lower extreme 320 and the upper extreme 967 are within the limits.
So, there are no outliers.
d.
To sketch: A box-and-whisker of the number of women’s teams playing a sport.
d.
Explanation of Solution
Given information:
The data is on the college tution and fees.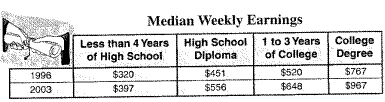 
Graph:
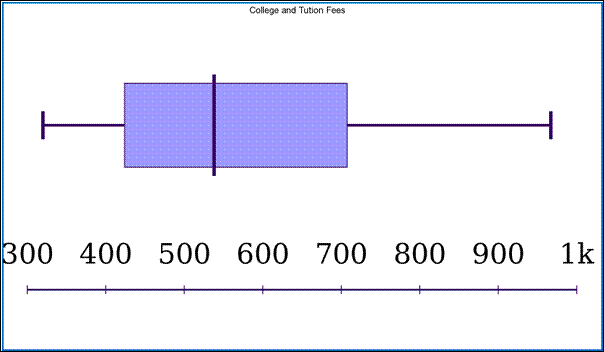
Interpretation:
The horizontal graph is known as box-and-whisker plots. It represents the data on the college tuition and fees. The median is 538. It does not have outliers.
e.
To calculate: The mean deviation of the data.
e.
Answer to Problem 23E
The mean deviation is 169.53125
Explanation of Solution
Given information:
The data is on the college tution and fees. 
Formula used:
The arithmetic mean of the absolute values of the deviations from the mean of a set of data is called the mean deviation.
MD=1nn∑i=1|Xi−ˉX|
Formula of Mean
ˉX=∑Xn where X represents each of the values in the data set.
Calculation:
Consider the data in ascending order ,
{$320,$397,$451,$520,$556,$648,$767,$967}.
So, n=8 .
There is even number of data.
The mean of the data is
=320+397+451+520+556+648+767+9678=578.25
The mean deviation is −
| Xi | ˉX | |Xi−ˉX| |
| 320 | 578.25 | =|320−578.25|=320 |
| 397 | 578.25 | =|397−578.25|=181.25 |
| 451 | 578.25 | =|451−578.25|=127.25 |
| 520 | 578.25 | =|520−578.25|=58.25 |
| 556 | 578.25 | =|556−578.25|=22.25 |
| 648 | 578.25 | =|648−578.25|=69.75 |
| 767 | 578.25 | =|767−578.25|=188.75 |
| 967 | 578.25 | =|967−578.25|=388.75 |
| 8∑i=1|Xi−ˉX| | 1356.25 | |
MD=18(1356.25) =169.53125
Hence, the mean deviation is 169.53125
f.
To calculate: The standard deviation of the data.
f.
Answer to Problem 23E
The standard deviation is 97461.55
Explanation of Solution
Given information:
The data is on the college tution and fees.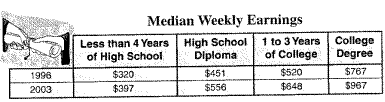 
Formula used:
A measure of variability associated with the arithmetic mean is the standard deviation.
σ=√1nn∑i=1(Xi−ˉX)2
Calculation:
Consider the data in ascending order ,
{$320,$397,$451,$520,$556,$648,$767,$967}.
So, n=8 .
There is even number of data.
The mean of the data is
=320+397+451+520+556+648+767+9678=578.25
The standard deviation is −
| Xi | ˉX | (Xi−ˉX) | (Xi−ˉX)2 |
| 320 | 578.25 | =320−578.25=−320 | 102400 |
| 397 | 578.25 | =397−578.25=−181.25 | 32851.5625 |
| 451 | 578.25 |
=451−578.25=−127.25 | 16192.5625 |
| 520 | 578.25 | =520−578.25=−58.25 | 3393.0625 |
| 556 | 578.25 | =556−578.25=−22.25 | 495.0625 |
| 648 | 578.25 | =648−578.25=69.75 | 4865.0625 |
| 767 | 578.25 | =767−578.25=188.75 | 35626.5625 |
| 967 | 578.25 | =967−578.25=388.75 | 151126.5625 |
| 8∑i=1|Xi−ˉX| | 346950.4375 | ||
=σ=√18(346950.4375)=σ=√43368.80=σ=208.251
Hence, the standard deviation is 208.251.
g.
To discuss: The variability of the data.
g.
Explanation of Solution
Given information:
The data is on the college tution and fees.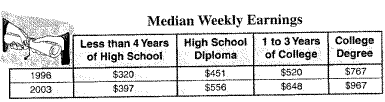 
Summary:
Variability of the data can be studied by box-and-whisker plot.
It represent the median, quartiles, interquartile range , and extreme values in a set of the data.
| Terms | 7 |
| Median | 538 |
| Q1 | 424 |
| Q3 | 707.5 |
| Interquartile | 283.5 |
| Semi-interquartile | 141.75 |
| Outliers | No |
Thus, the box-and-whisker drawn in previous part is a pictorial representation of the variability of the data.
Chapter 14 Solutions
Advanced Mathematical Concepts: Precalculus with Applications, Student Edition
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics (13th Edition)
University Calculus: Early Transcendentals (4th Edition)
Thinking Mathematically (6th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
- (14 points) Let S = {(x, y, z) | z = e−(x²+y²), x² + y² ≤ 1}. The surface is the graph of ze(+2) sitting over the unit disk.arrow_forward6. Solve the system of differential equations using Laplace Transforms: x(t) = 3x₁ (t) + 4x2(t) x(t) = -4x₁(t) + 3x2(t) x₁(0) = 1,x2(0) = 0arrow_forward3. Determine the Laplace Transform for the following functions. Show all of your work: 1-t, 0 ≤t<3 a. e(t) = t2, 3≤t<5 4, t≥ 5 b. f(t) = f(tt)e-3(-) cos 4τ drarrow_forward
- 4. Find the inverse Laplace Transform Show all of your work: a. F(s) = = 2s-3 (s²-10s+61)(5-3) se-2s b. G(s) = (s+2)²arrow_forward1. Consider the differential equation, show all of your work: dy =(y2)(y+1) dx a. Determine the equilibrium solutions for the differential equation. b. Where is the differential equation increasing or decreasing? c. Where are the changes in concavity? d. Suppose that y(0)=0, what is the value of y as t goes to infinity?arrow_forward2. Suppose a LC circuit has the following differential equation: q'+4q=6etcos 4t, q(0) = 1 a. Find the function for q(t), use any method that we have studied in the course. b. What is the transient and the steady-state of the circuit?arrow_forward
- 5. Use variation of parameters to find the general solution to the differential equation: y" - 6y' + 9y=e3x Inxarrow_forwardLet the region R be the area enclosed by the function f(x) = ln (x) + 2 and g(x) = x. Write an integral in terms of x and also an integral in terms of y that would represent the area of the region R. If necessary, round limit values to the nearest thousandth. 5 4 3 2 1 y x 1 2 3 4arrow_forward(28 points) Define T: [0,1] × [−,0] → R3 by T(y, 0) = (cos 0, y, sin 0). Let S be the half-cylinder surface traced out by T. (a) (4 points) Calculate the normal field for S determined by T.arrow_forward
- (14 points) Let S = {(x, y, z) | z = e−(x²+y²), x² + y² ≤ 1}. The surface is the graph of ze(+2) sitting over the unit disk. = (a) (4 points) What is the boundary OS? Explain briefly. (b) (4 points) Let F(x, y, z) = (e³+2 - 2y, xe³±² + y, e²+y). Calculate the curl V × F.arrow_forward(6 points) Let S be the surface z = 1 − x² - y², x² + y² ≤1. The boundary OS of S is the unit circle x² + y² = 1. Let F(x, y, z) = (x², y², z²). Use the Stokes' Theorem to calculate the line integral Hint: First calculate V x F. Jos F F.ds.arrow_forward(28 points) Define T: [0,1] × [−,0] → R3 by T(y, 0) = (cos 0, y, sin 0). Let S be the half-cylinder surface traced out by T. (a) (4 points) Calculate the normal field for S determined by T.arrow_forward
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning