
Concept explainers
Interpretation:
The energies of rotation for ammonia,
Concept introduction:
Atoms of a molecule rotate in space about its moment of inertia. The rotational quantum number is represented by the symbol
Answer to Problem 14.98E
The energies of rotation for ammonia,
| 1 | -1 | 3753.185 |
| 1 | 0 | 1264.06 |
| 1 | 1 | 3753.185 |
| 2 | -2 | 13748.68 |
| 2 | -1 | 6281.305 |
| 2 | 0 | 3792.18 |
| 2 | 1 | 6281.305 |
| 2 | 2 | 13748.68 |
| 3 | -3 | 29986.49 |
| 3 | -2 | 17540.86 |
| 3 | -1 | 10073.49 |
| 3 | 0 | 7584.36 |
| 3 | 1 | 10073.49 |
| 3 | 2 | 17540.86 |
| 3 | 3 | 29986.49 |
| 4 | -4 | 52466.6 |
| 4 | -3 | 35042.73 |
| 4 | -2 | 22597.1 |
| 4 | -1 | 15129.73 |
| 4 | 0 | 12640.6 |
| 4 | 1 | 15129.73 |
| 4 | 2 | 22597.1 |
| 4 | 3 | 52466.6 |
| 4 | 4 | 52466.6 |
| 5 | -5 | 81189.03 |
| 5 | -4 | 58786.9 |
| 5 | -3 | 41363.03 |
| 5 | -2 | 28917.4 |
| 5 | -1 | 21450.03 |
| 5 | 0 | 18960.9 |
| 5 | 1 | 21450.03 |
| 5 | 2 | 28917.4 |
| 5 | 3 | 41363.03 |
| 5 | 4 | 58786.9 |
| 5 | 5 | 81189.03 |
| 6 | -6 | 116153.8 |
| 6 | -5 | 88773.39 |
| 6 | -4 | 66371.26 |
| 6 | -3 | 48947.39 |
| 6 | -2 | 36501.76 |
| 6 | -1 | 29034.39 |
| 6 | 0 | 26545.26 |
| 6 | 1 | 29034.39 |
| 6 | 2 | 36501.76 |
| 6 | 3 | 48947.39 |
| 6 | 4 | 66371.26 |
| 6 | 5 | 88773.39 |
| 6 | 6 | 116153.8 |
| 7 | -7 | 157360.8 |
| 7 | -6 | 125002.2 |
| 7 | -5 | 97621.81 |
| 7 | -4 | 75219.68 |
| 7 | -3 | 57795.81 |
| 7 | -2 | 45350.18 |
| 7 | -1 | 37882.81 |
| 7 | 0 | 35393.68 |
| 7 | 1 | 37882.81 |
| 7 | 2 | 45350.18 |
| 7 | 3 | 57795.81 |
| 7 | 4 | 75219.68 |
| 7 | 5 | 97621.81 |
| 7 | 6 | 125002.2 |
| 7 | 7 | 157360.8 |
| 8 | -8 | 204810.2 |
| 8 | -7 | 167473.3 |
| 8 | -6 | 135114.7 |
| 8 | -5 | 107734.3 |
| 8 | -4 | 85332.16 |
| 8 | -3 | 67908.29 |
| 8 | -2 | 55462.66 |
| 8 | -1 | 47995.29 |
| 8 | 0 | 45506.16 |
| 8 | 1 | 47995.29 |
| 8 | 2 | 55462.66 |
| 8 | 3 | 67908.29 |
| 8 | 4 | 85332.16 |
| 8 | 5 | 107734.3 |
| 8 | 6 | 135114.7 |
| 8 | 7 | 167473.3 |
| 8 | 8 | 204810.2 |
| 9 | -9 | 258501.8 |
| 9 | -8 | 216186.7 |
| 9 | -7 | 178849.8 |
| 9 | -6 | 146491.2 |
| 9 | -5 | 119110.8 |
| 9 | -4 | 96708.7 |
| 9 | -3 | 79284.83 |
| 9 | -2 | 66839.2 |
| 9 | -1 | 59371.83 |
| 9 | 0 | 56882.7 |
| 9 | 1 | 59371.83 |
| 9 | 2 | 66839.2 |
| 9 | 3 | 79284.83 |
| 9 | 4 | 96708.7 |
| 9 | 5 | 119110.8 |
| 9 | 6 | 146491.2 |
| 9 | 7 | 178849.8 |
| 9 | 8 | 216186.7 |
| 9 | 9 | 258501.8 |
| 10 | -10 | 318435.8 |
| 10 | -9 | 271142.4 |
| 10 | -8 | 228827.3 |
| 10 | -7 | 191490.4 |
| 10 | -6 | 159131.8 |
| 10 | -5 | 131751.4 |
| 10 | -4 | 109349.3 |
| 10 | -3 | 91925.43 |
| 10 | -2 | 79479.8 |
| 10 | -1 | 72012.43 |
| 10 | 0 | 69523.3 |
| 10 | 1 | 72012.43 |
| 10 | 2 | 79479.8 |
| 10 | 3 | 91925.43 |
| 10 | 4 | 109349.3 |
| 10 | 5 | 131751.4 |
| 10 | 6 | 159131.8 |
| 10 | 7 | 191490.4 |
| 10 | 8 | 228827.3 |
| 10 | 9 | 271142.4 |
| 10 | 10 | 318435.8 |
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
For the rotational quantum number
The energy level diagram for all the rotational levels is shown below.
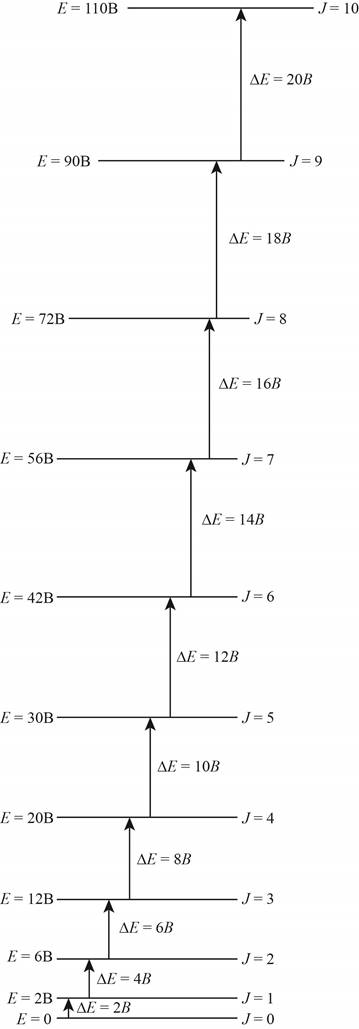
Explanation of Solution
The formula to energy of rotation (
Where,
•
•
The formula for
The formula for
Where,
•
•
The value of
Substitute the value of
The value of
Substitute the value of
The value of
The degeneracy is calculated by the formula given below.
For the rotational quantum number
The value of
The value of
Substitute the value of
Therefore, the degeneracy is
Substitute the value of
Similarly the value of
| 1 | -1 | 3753.185 |
| 1 | 0 | 1264.06 |
| 1 | 1 | 3753.185 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 2 | -2 | 13748.68 |
| 2 | -1 | 6281.305 |
| 2 | 0 | 3792.18 |
| 2 | 1 | 6281.305 |
| 2 | 2 | 13748.68 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 3 | -3 | 29986.49 |
| 3 | -2 | 17540.86 |
| 3 | -1 | 10073.49 |
| 3 | 0 | 7584.36 |
| 3 | 1 | 10073.49 |
| 3 | 2 | 17540.86 |
| 3 | 3 | 29986.49 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 4 | -4 | 52466.6 |
| 4 | -3 | 35042.73 |
| 4 | -2 | 22597.1 |
| 4 | -1 | 15129.73 |
| 4 | 0 | 12640.6 |
| 4 | 1 | 15129.73 |
| 4 | 2 | 22597.1 |
| 4 | 3 | 52466.6 |
| 4 | 4 | 52466.6 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 5 | -5 | 81189.03 |
| 5 | -4 | 58786.9 |
| 5 | -3 | 41363.03 |
| 5 | -2 | 28917.4 |
| 5 | -1 | 21450.03 |
| 5 | 0 | 18960.9 |
| 5 | 1 | 21450.03 |
| 5 | 2 | 28917.4 |
| 5 | 3 | 41363.03 |
| 5 | 4 | 58786.9 |
| 5 | 5 | 81189.03 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 6 | -6 | 116153.8 |
| 6 | -5 | 88773.39 |
| 6 | -4 | 66371.26 |
| 6 | -3 | 48947.39 |
| 6 | -2 | 36501.76 |
| 6 | -1 | 29034.39 |
| 6 | 0 | 26545.26 |
| 6 | 1 | 29034.39 |
| 6 | 2 | 36501.76 |
| 6 | 3 | 48947.39 |
| 6 | 4 | 66371.26 |
| 6 | 5 | 88773.39 |
| 6 | 6 | 116153.8 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 7 | -7 | 157360.8 |
| 7 | -6 | 125002.2 |
| 7 | -5 | 97621.81 |
| 7 | -4 | 75219.68 |
| 7 | -3 | 57795.81 |
| 7 | -2 | 45350.18 |
| 7 | -1 | 37882.81 |
| 7 | 0 | 35393.68 |
| 7 | 1 | 37882.81 |
| 7 | 2 | 45350.18 |
| 7 | 3 | 57795.81 |
| 7 | 4 | 75219.68 |
| 7 | 5 | 97621.81 |
| 7 | 6 | 125002.2 |
| 7 | 7 | 157360.8 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 8 | -8 | 204810.2 |
| 8 | -7 | 167473.3 |
| 8 | -6 | 135114.7 |
| 8 | -5 | 107734.3 |
| 8 | -4 | 85332.16 |
| 8 | -3 | 67908.29 |
| 8 | -2 | 55462.66 |
| 8 | -1 | 47995.29 |
| 8 | 0 | 45506.16 |
| 8 | 1 | 47995.29 |
| 8 | 2 | 55462.66 |
| 8 | 3 | 67908.29 |
| 8 | 4 | 85332.16 |
| 8 | 5 | 107734.3 |
| 8 | 6 | 135114.7 |
| 8 | 7 | 167473.3 |
| 8 | 8 | 204810.2 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 9 | -9 | 258501.8 |
| 9 | -8 | 216186.7 |
| 9 | -7 | 178849.8 |
| 9 | -6 | 146491.2 |
| 9 | -5 | 119110.8 |
| 9 | -4 | 96708.7 |
| 9 | -3 | 79284.83 |
| 9 | -2 | 66839.2 |
| 9 | -1 | 59371.83 |
| 9 | 0 | 56882.7 |
| 9 | 1 | 59371.83 |
| 9 | 2 | 66839.2 |
| 9 | 3 | 79284.83 |
| 9 | 4 | 96708.7 |
| 9 | 5 | 119110.8 |
| 9 | 6 | 146491.2 |
| 9 | 7 | 178849.8 |
| 9 | 8 | 216186.7 |
| 9 | 9 | 258501.8 |
For the rotational quantum number
Substitute the value of
Therefore, the degeneracy is
Similarly the value of
| 10 | -10 | 318435.8 |
| 10 | -9 | 271142.4 |
| 10 | -8 | 228827.3 |
| 10 | -7 | 191490.4 |
| 10 | -6 | 159131.8 |
| 10 | -5 | 131751.4 |
| 10 | -4 | 109349.3 |
| 10 | -3 | 91925.43 |
| 10 | -2 | 79479.8 |
| 10 | -1 | 72012.43 |
| 10 | 0 | 69523.3 |
| 10 | 1 | 72012.43 |
| 10 | 2 | 79479.8 |
| 10 | 3 | 91925.43 |
| 10 | 4 | 109349.3 |
| 10 | 5 | 131751.4 |
| 10 | 6 | 159131.8 |
| 10 | 7 | 191490.4 |
| 10 | 8 | 228827.3 |
| 10 | 9 | 271142.4 |
| 10 | 10 | 318435.8 |
The energy level diagram for all the rotational levels is shown below.
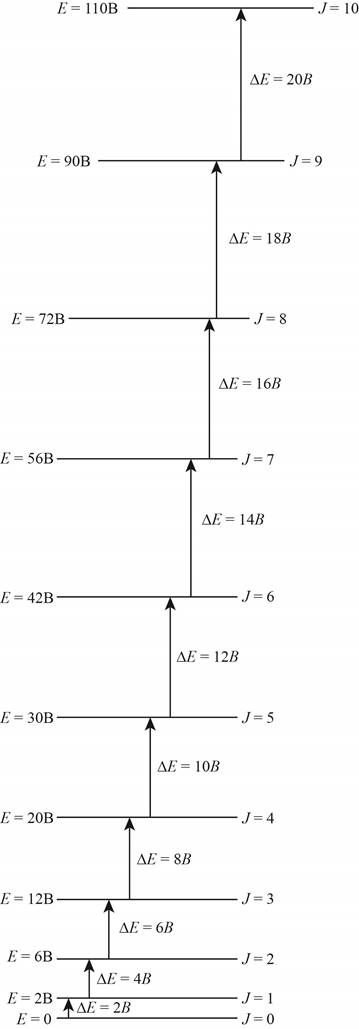
Figure 1
The energies of rotation for ammonia,
Want to see more full solutions like this?
Chapter 14 Solutions
Physical Chemistry
- Experiment 27 hates & Mechanisms of Reations Method I visual Clock Reaction A. Concentration effects on reaction Rates Iodine Run [I] mol/L [S₂082] | Time mo/L (SCC) 0.04 54.7 Log 1/ Time Temp Log [ ] 13,20] (time) / [I] 199 20.06 23.0 30.04 0.04 0.04 80.0 22.8 45 40.02 0.04 79.0 21.6 50.08 0.03 51.0 22.4 60-080-02 95.0 23.4 7 0.08 0-01 1970 23.4 8 0.08 0.04 16.1 22.6arrow_forward(15 pts) Consider the molecule B2H6. Generate a molecular orbital diagram but this time using a different approach that draws on your knowledge and ability to put concepts together. First use VSEPR or some other method to make sure you know the ground state structure of the molecule. Next, generate an MO diagram for BH2. Sketch the highest occupied and lowest unoccupied MOs of the BH2 fragment. These are called frontier orbitals. Now use these frontier orbitals as your basis set for producing LGO's for B2H6. Since the BH2 frontier orbitals become the LGOS, you will have to think about what is in the middle of the molecule and treat its basis as well. Do you arrive at the same qualitative MO diagram as is discussed in the book? Sketch the new highest occupied and lowest unoccupied MOs for the molecule (B2H6).arrow_forwardQ8: Propose an efficient synthesis of cyclopentene from cyclopentane.arrow_forward
- Q7: Use compound A-D, design two different ways to synthesize E. Which way is preferred? Please explain. CH3I ONa NaOCH 3 A B C D E OCH3arrow_forwardPredict major product(s) for the following reactions. Note the mechanism(s) of the reactions (SN1, E1, SN2 or E2).arrow_forward(10 pts) The density of metallic copper is 8.92 g cm³. The structure of this metal is cubic close-packed. What is the atomic radius of copper in copper metal?arrow_forward
- Predict major product(s) for the following reactions. Note the mechanism(s) of the reactions (SN1, E1, SN2 or E2).arrow_forwardPredict major product(s) for the following reactions. Note the mechanism(s) of the reactions (SN1, E1, SN2 or E2).arrow_forwardQ3: Rank the following compounds in increasing reactivity of E1 and E2 eliminations, respectively. Br ca. go do A CI CI B C CI Darrow_forward
- Q5: Predict major product(s) for the following reactions. Note the mechanism(s) of the reactions (SN1, E1, SN2 or E2). H₂O דיי "Br KN3 CH3CH2OH NaNH2 NH3 Page 3 of 6 Chem 0310 Organic Chemistry 1 HW Problem Sets CI Br excess NaOCH 3 CH3OH Br KOC(CH3)3 DuckDuckGarrow_forwardQ4: Circle the substrate that gives a single alkene product in a E2 elimination. CI CI Br Brarrow_forwardPlease calculate the chemical shift of each protonsarrow_forward
 Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning
Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,
Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,

