Chapter 4.3, Problem 36E

(a)

To determine

To find : The vertical and horizontal asymptotes.

Explanation of Solution

Given: The function is $f\left(x\right)=x\tan x$

Consider the function.

  $f\left(x\right)=x\tan x$

The horizontal asymptote is not defined.

The vertical asymptote is calculated as,

  $\begin{array}{c}\underset{x\to {\frac{\pi }{2}}^{+}}{\lim }f\left(x\right)=\underset{x\to {\frac{\pi }{2}}^{+}}{\lim }x\tan x\\ =\underset{x\to {\frac{\pi }{2}}^{+}}{\lim }x\cdot \underset{x\to {\frac{\pi }{2}}^{+}}{\lim }\tan x\\ =\infty \end{array}$

And,

  $\begin{array}{c}\underset{x\to {\frac{\pi }{2}}^{-}}{\lim }f\left(x\right)=\underset{x\to {\frac{\pi }{2}}^{-}}{\lim }x\tan x\\ =\underset{x\to {\frac{\pi }{2}}^{-}}{\lim }x\cdot \underset{x\to {\frac{\pi }{2}}^{-}}{\lim }\tan x\\ =-\infty \end{array}$

So, the vertical asymptotes are $x=\pm \frac{\pi }{2}$ .

(b)

To determine

To find : The interval of increase or decrease.

Explanation of Solution

Given: The function is $f\left(x\right)=x\tan x$

Consider the function.

  $f\left(x\right)=x\tan x$

Differentiate the above expression with respect to $x$ .

  $f^{\prime }\left(x\right)=x{\sec }^{2}x+\tan x$

The function is decreasing in the interval $\left(-\frac{\pi }{2},0\right)$

The function is increasing in the interval $\left(0,\frac{\pi }{2}\right)$

(c)

To determine

To find : The local maximum and minimum values..

Explanation of Solution

Given: The function is $f\left(x\right)=x\tan x$

The function is decreasing in the interval $\left(-\frac{\pi }{2},0\right)$

The function is increasing in the interval $\left(0,\frac{\pi }{2}\right)$

So, the function is minimum at $x=0$ and the local maxima is $\left(0,f\left(0\right)\right)=\left(0,0\right)$ .

There is no local maxima.

(d)

To determine

To find : The intervals of concavity and the inflection points.

Explanation of Solution

Given: The function is $f\left(x\right)=x\tan x$

Differentiate $f^{\prime }\left(x\right)$ with respect to $x$ .

  $\begin{array}{c}{f}^{″}\left(x\right)=x\left(2\sec x\right)\left(\sec x\tan x\right)+2{\sec }^{2}x\\ =2x{\sec }^{2}x\tan x+2{\sec }^{2}x\end{array}$

The value of $f^{″}\left(c\right)$ is positive for $-\frac{\pi }{2}<x<\frac{\pi }{2}$ . So the concavity is upward in the interval $\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ .

The function has no inflection point.

(e)

To determine

To sketch : The graph of the function.

Explanation of Solution

Given: The function is $f\left(x\right)=x\tan x$

Consider the function.

  $f\left(x\right)=x\tan x$

The graph of the above function is shown in figure below.

  

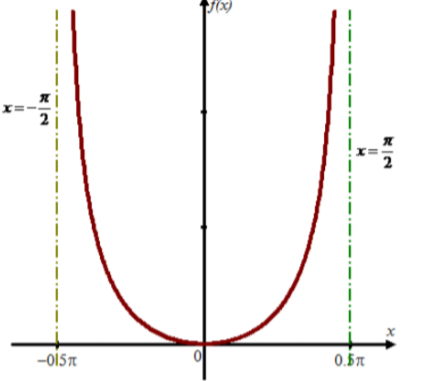
Figure (1)

Therefore, the graph of the function is shown in Figure (1).