Concept explainers
Videos
(a)
To find: Thevertical and horizontal asymptote of the function.
(a)
Answer to Problem 10RE
The Horizontal asymptote is y=0 and vertical asymptote is x=1.
Explanation of Solution
Given: f(x)=11-x2 .
Concept used:
If the degree of the numerator is less than the denominator, thehorizontal asymptote is
y=0 .
If the denominator has no zeroes then there has no vertical asymptotes
Or
To get Vertical asymptote function should be rational and denominator must contain some variable otherwise there has no vertical asymptote.
Calculation:
Accordingto the laws of asymptotes:
If the degree of the numerator is more than the denominator, there is no horizontal asymptote.
If the denominator has no zeroes then there has no vertical asymptotes/.
Here the numerator of the function has degree 1 and denominator has degree of 2.
the horizontal asymptote is y=0 and Vertical asymptote is denominator equal to zero.
1−x2=0
−x2=−1
x=1.
Vertical asymptote is at x=1.
Hence, the Horizontal asymptote is y=0 and vertical asymptote is x=1.
(b)
To find: TheInterval of increasing or decreasing of the function.
(b)
Answer to Problem 10RE
The Interval of increasing or decreasing of the function is
(−∞,−3),(−3,0),(0,3) .
Decreasing at interval of (−∞,−3) .
Increasing at interval of (−3,0),(0,3) .
Explanation of Solution
Given: f(x)=11-x2 .
Concept used:
Increasing or decreasing function can be calculated by equating first derivative of the function to 0.
dydx=0 .
Zeroes of x can be calculatedafter that the increasing and decreasing can be measured.
Calculation:
Increasing or decreasing function can be calculated by equating first derivative of the function to 0.
dydx=0 .
dydx=(1-x2)(0)-1(-2x)(1-x2)2=2x(1-x2)2
dydx=2x(1-x2)2
2x(1-x2)2=0
x=0 .
Hence the Interval of increasing or decreasing of the function is
(−∞,0) and (0,∞). .
Decreasing at interval of (−∞,0) .
Increasing at interval of (0,∞) .
(c)
To find: The
(c)
Answer to Problem 10RE
x=0 and y=1 are the point of local
the point of inflection at x=0 .
Explanation of Solution
Given: f(x)=11-x2 .
Concept used:
The local maxima and minima can be calculated by firstly equating the double differentiation to 0.
1. d2ydx2=0.
2.If d2ydx2>0. the concave will be open upward and local minima can be found.
3. d2ydx2<0. the concave will open downward and local maxima can be found.
Calculation:
f(x)=11-x2
dydx=2x(1-x2)2
2x(1-x2)2=0
x=0 .
d2ydx2=(1-x2)2.2+2.2x.2(1-x2)(1-x2)4=2(1-x2)2+8x(1-x2)(1-x2)4=2(1-x2)+8x(1-x2)3.
d2ydx2=2(1-x2)+8x(1-x2)3
At x=0 ,
d2ydx2=2(1-(0)2)+8(0)(1-(0)2)3=2.
d2ydx2=2.
d2ydx2>0.
Hence, x=0 and y=1 are the point of local maxima and there is no
Local minima.
the point of inflection at x=0 .
(d)
To find: The interval of concavity and the inflection point.
(d)
Answer to Problem 10RE
Concave downward in the interval of (−∞,−2) .
Concave upward in the interval of (−2,0), (0,∞) .
These points are point of inflection
x=0,x=−2 .
Explanation of Solution
Given: f(x)=11-x2 .
Concept used:
The second derivative of function is calculated first.
Set the second derivative equal to zero and solve.
Check whether the second derivative undefined for any values of x.
Plot the number on number line and test the regions with the second derivative.
Plug these 3 values for obtain three inflection points.
The graph of y=f(x) is concave upward on those intervals where
y=f″(x)>0 .
The graph of y=f(x) id concave downward on thoseintervals where
y=f″(x)<0 .
If the graph of y=f(x) has point of inflection then y=f″(x)=0 .
Calculation:
d2ydx2=2(1-x2)+8x(1-x2)3
d2ydx2=2(1-x2)+8x(1-x2)3=0.
2(1-x2)+8x=0.
2−2x2+8x=0.
1−x2+4x=0
x2−4x−1=0 .
a=1, b=-4, c=-1.
x=4±√16+42=4±√202=4±2√52 .
x=2(2±1√5)2=2±1√5.
x=2+1√5, x=2-1√5.
This two are the point of inflection.
By putting the values in the equation.
The interval will be (−∞,2−1√5), (2−1√5,2+1√5), (2+1√5,∞) .
Hence,
Concave downward in the interval of (−∞,−2) .
Concave upward in the interval of (−2,0), (0,∞) .
These points are point of inflection
x=0,x=−2 .
(e)
To Sketch:the graph of the function using graphing device.
(e)
Answer to Problem 10RE
Through the graph it’s easily verified the point of local maxima and minima, function is increasing or decreasing, concavity down or up and point of inflection.
Explanation of Solution
Given: f(x)=11-x2 .
Concept used:
Desmos graphing calculator is used her to plot the graph and it can easily verify the maxima, minima and point of inflection etc.
Calculation:
The graph of f(x)=11-x2
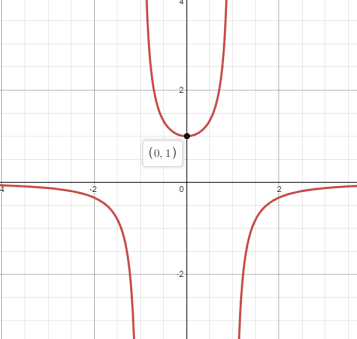
Hence, through the graph it’s easily verified the point of local maxima and minima, function is increasing or decreasing, concavity down or up and point of inflection.
Chapter 4 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
- A factorization A = PDP 1 is not unique. For A= 7 2 -4 1 1 1 5 0 2 1 one factorization is P = D= and P-1 30 = Use this information with D₁ = to find a matrix P₁ such that - -1 -2 0 3 1 - - 1 05 A-P,D,P P1 (Type an integer or simplified fraction for each matrix element.)arrow_forwardMatrix A is factored in the form PDP 1. Use the Diagonalization Theorem to find the eigenvalues of A and a basis for each eigenspace. 30 -1 - 1 0 -1 400 0 0 1 A= 3 4 3 0 1 3 040 3 1 3 0 0 4 1 0 0 003 -1 0 -1 Select the correct choice below and fill in the answer boxes to complete your choice. (Use a comma to separate vectors as needed.) A basis for the corresponding eigenspace is { A. There is one distinct eigenvalue, λ = B. In ascending order, the two distinct eigenvalues are λ₁ ... = and 2 = Bases for the corresponding eigenspaces are { and ( ), respectively. C. In ascending order, the three distinct eigenvalues are λ₁ = = 12/2 = and 3 = Bases for the corresponding eigenspaces are {}, }, and { respectively.arrow_forwardN Page 0.6. 0.4. 0.2- -0.2- -0.4- -6.6 -5 W 10arrow_forward
- Diagonalize the following matrix, if possible. 8 0 6 - 8 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. 8 0 OA. For P= D= 0 3 6 0 B. For P = D= 0 -6 8 0 C. For P = D= 0 - 8 D. The matrix cannot be diagonalized.arrow_forwardCalculus lll May I please have the solutions for the following exercises? Thank youarrow_forwardCalculus lll May I please have the solution for the following question? Thank youarrow_forward
- Find three horizontal tangents between [0,10]arrow_forward4 In the integral dxf1dy (7)², make the change of variables x = ½(r− s), y = ½(r + s), and evaluate the integral. Hint: Find the limits on r and s by sketching the area of integration in the (x, y) plane along with the r and s axes, and then show that the same area can be covered by s from 0 to r and r from 0 to 1.arrow_forward7. What are all values of 0, for 0≤0<2л, where 2 sin² 0=-sin? - 5π 6 π (A) 0, л, and 6 7π (B) 0,л, 11π , and 6 6 π 3π π (C) 5π 2 2 3 , and π 3π 2π (D) 2' 2'3 , and 3 4元 3 1 די } I -2m 3 1 -3 บ 1 # 1 I 3# 3m 8. The graph of g is shown above. Which of the following is an expression for g(x)? (A) 1+ tan(x) (B) 1-tan (x) (C) 1-tan (2x) (D) 1-tan + X - 9. The function j is given by j(x)=2(sin x)(cos x)-cos x. Solve j(x) = 0 for values of x in the interval Quiz A: Topic 3.10 Trigonometric Equations and Inequalities Created by Bryan Passwaterarrow_forward
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning