Chapter 4.3, Problem 27E

(a)

To determine

To find:The intervals of increase or decrease.

Explanation of Solution

Given: $A\left(x\right)=x\sqrt{x+3}$

Calculate the first derivative of the given function.

  $\begin{array}{c}{A}^{\prime }\left(x\right)=\sqrt{x+3}+x\cdot \frac{1}{2\sqrt{x+3}}\\ =\frac{2\left(x+3\right)+x}{2\sqrt{x+3}}\\ =\frac{2x+6+x}{2\sqrt{x+3}}\end{array}$

Equate to zero.

  $x=-2,-3$

The function is decreasing in the interval $\left(-3,-2\right)$ .

The function is increasing in the interval $\left(-2,\infty \right)$

(b)

To determine

To find :The local maxima and local minima.

Explanation of Solution

The function is decreasing in the interval $\left(-3,-2\right)$ .

The function is increasing in the interval $\left(-2,\infty \right)$

The value of $A^{\prime }$ is changing from negative to positive at $x=-2$

So, the local minima is $\left(-2,-2\right)$

There is no local maxima.

(c)

To determine

To find:The concavity of the function and the point of inflection.

Explanation of Solution

Calculate the second derivative of the given function.

  $\begin{array}{c}{A}^{″}\left(x\right)=\frac{3}{2}\left[\frac{x+4}{2\left(x+3\right)\sqrt{x+3}}\right]\\ =\frac{3}{4}\left[\frac{x+4}{{\left(x+3\right)}^{3/2}}\right]\end{array}$

  $A^{″}\left(x\right)>0$ for the interval $-3<x<ki$ . So, the graph is concave up for $\left(-3,\infty \right)$

There is no change of sign so no inflection point.

(d)

To determine

To sketch :The graph of result obtained from part (a) to (c).

Explanation of Solution

Given: $A\left(x\right)=x\sqrt{x+3}$

The graph of the result obtained is shown in figure below.

  

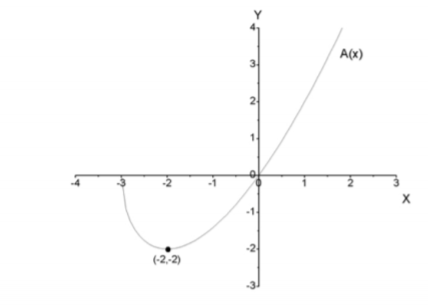
Figure (1)

Therefore, the required graph is shown in figure (1).