Introduction to Algorithms
3rd Edition
ISBN: 9780262033848
Author: Thomas H. Cormen, Ronald L. Rivest, Charles E. Leiserson, Clifford Stein
Publisher: MIT Press
expand_more
expand_more
format_list_bulleted
Question
Chapter 24.4, Problem 8E
Program Plan Intro
To show that Bellman-Ford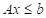 
graph then it maximizes the value function 
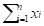for 
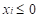
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Given a system of difference constraints. Let G=(V,E) be the corresponding constraint graph. By applying BELLMAN_FORD's algorithm on v0 (v0 is the source vertex), the number of vertices who's shortest paths will be updated is at the second iteration.
x1 - x2 ≤ 7
x1 - x3 ≤ 6
x2 - x4 ≤ -3
x3 - x4 ≤ -2
x4 - x1 ≤ -3
We know that when we have a graph with negative edge costs, Dijkstra’s algorithm is not guaranteed to work.
(a) Does Dijkstra’s algorithm ever work when some of the edge costs are negative? Explain why or why not.
(b) Find an algorithm that will always find a shortest path between two nodes, under the assumption that at most one edge in the input has a negative weight. Your algorithm should run in time O(m log n), where m is the number of edges and n is the number of nodes. That is, the runnning time should be at most a constant factor slower than Dijkstra’s algorithm. To be clear, your algorithm takes as input
(i) a directed graph, G, given in adjacency list form. (ii) a weight function f, which, given two adjacent nodes, v,w, returns the weight of the edge between them. For non-adjacent nodes v,w, you may assume f(v,w) returns +1. (iii) a pair of nodes, s, t. If the input contains a negative cycle, you should find one and output it. Otherwise, if the graph contains at least one…
he heuristic path algorithm is a best-first search in which the objective function is f(n) = (4 −w)g(n) + wh(n). For what values of w is this algorithm guaranteed to be optimal? What kind of search does this perform when w = 0? When w = 1? When w = 4?
Chapter 24 Solutions
Introduction to Algorithms
Ch. 24.1 - Prob. 1ECh. 24.1 - Prob. 2ECh. 24.1 - Prob. 3ECh. 24.1 - Prob. 4ECh. 24.1 - Prob. 5ECh. 24.1 - Prob. 6ECh. 24.2 - Prob. 1ECh. 24.2 - Prob. 2ECh. 24.2 - Prob. 3ECh. 24.2 - Prob. 4E
Ch. 24.3 - Prob. 1ECh. 24.3 - Prob. 2ECh. 24.3 - Prob. 3ECh. 24.3 - Prob. 4ECh. 24.3 - Prob. 5ECh. 24.3 - Prob. 6ECh. 24.3 - Prob. 7ECh. 24.3 - Prob. 8ECh. 24.3 - Prob. 9ECh. 24.3 - Prob. 10ECh. 24.4 - Prob. 1ECh. 24.4 - Prob. 2ECh. 24.4 - Prob. 3ECh. 24.4 - Prob. 4ECh. 24.4 - Prob. 5ECh. 24.4 - Prob. 6ECh. 24.4 - Prob. 7ECh. 24.4 - Prob. 8ECh. 24.4 - Prob. 9ECh. 24.4 - Prob. 10ECh. 24.4 - Prob. 11ECh. 24.4 - Prob. 12ECh. 24.5 - Prob. 1ECh. 24.5 - Prob. 2ECh. 24.5 - Prob. 3ECh. 24.5 - Prob. 4ECh. 24.5 - Prob. 5ECh. 24.5 - Prob. 6ECh. 24.5 - Prob. 7ECh. 24.5 - Prob. 8ECh. 24 - Prob. 1PCh. 24 - Prob. 2PCh. 24 - Prob. 3PCh. 24 - Prob. 4PCh. 24 - Prob. 5PCh. 24 - Prob. 6P
Knowledge Booster
Similar questions
- Problem 5 R y. Let G be a connected weighted undirected graph with n nodes and m edges. The weight of edge e is represented as we. We define a minimum-maximum spanning tree to be a spanning tree T that minimizes the quantity Y = max we eeT A minimum-maximum spanning tree has the smallest maximum edge weight of all possible spanning tree. To show a statement is correct, you need to provide a proof. To show a statement is wrong, you only need to provide a counter-example. (a) maximum spanning tree for G. Prove that a minimum spanning tree of graph G is always a minimum- Show that a minimum-maximum spanning tree is not necessary a minimum (b) spanning tree.arrow_forwardDemonstrate that the decision problem variant is NP-complete; Exists, given a graph G and a cost objective c, a spanning tree where the maximum payment of any vertex does not exceed c?arrow_forwardP is the set of problems that can be solved in polynomial time. More formally, P is the set of decision problems (e.g. given a graph G, does this graph G contain an odd cycle) for which there exists a polynomial-time algorithm to correctly output the answer to that problem. What is NP? Consider these five options and determine which option is correct. O NP is the set of problems that cannot be solved in polynomial time. NP is the set of problems whose answer can be found in polynomial time. O NP is the set of problems whose answer cannot be found in polynomial time. O NP is the set of problems that can be verified in polynomial time. O NP is the set of problems that cannot be verified in polynomial time.arrow_forward
- L = {f in SAT | the number of satisfying assignments of f > 1/2 |f| } Show that L is NP-completearrow_forwardQuestion 2: Consider the 0/1 knapsack problem. Given Nobjects where each object is specified by a weight and a profit, you are to put the objects in a bag of capacity C such that the sum of weights of the items in the bag does not exceed Cand the profits of the items is maximized. Note that you cannot use an item type more than once. a. Using dynamic programming, write an algorithm that finds the maximum total value according to the above constraints. b. What is the complexity of your algorithm? c. Show the dynamic programming table for the following data: W= { 2 ,7 , 1} , P={ 3 ,15 , 2 } and C=8.arrow_forwardPlease answer the following question in full detail. Please be specifix about everything: You have learned before that A∗ using graph search is optimal if h(n) is consistent. Does this optimality still hold if h(n) is admissible but inconsistent? Using the graph in Figure 1, let us now show that A∗ using graph search returns the non-optimal solution path (S,B,G) from start node S to goal node G with an admissible but inconsistent h(n). We assume that h(G) = 0. Give nonnegative integer values for h(A) and h(B) such that A∗ using graph search returns the non-optimal solution path (S,B,G) from S to G with an admissible but inconsistent h(n), and tie-breaking is not needed in A∗.arrow_forward
- P is the set of problems that can be solved in polynomial time. More formally, P is the set of decision problems (e.g. given a graph G, does this graph G contain an odd cycle) for which there exists a polynomial-time algorithm to correctly output the answer to that problem. What is NP? Consider these five options. A. NP is the set of problems that cannot be solved in polynomial time. B. NP is the set of problems whose answer can be found in polynomial time. C. NP is the set of problems whose answer cannot be found in polynomial time. D. NP is the set of problems that can be verified in polynomial time. E. NP is the set of problems that cannot be verified in polynomial time. Determine which option is correct. Answer either A, B, C, D, or E.arrow_forwardPlease assist with the following question as I am struggling. Thank you!arrow_forwardHow would you modify the dynamic programming algorithm for the coin collecting problem if some cells on the board are inaccessible for the robot? Apply your algorithm to the board below, where the inaccessible cells are shown by X’s. How many optimal paths are there for this board? You need to provide 1) a modified recurrence relation, 2) a pseudo code description of the algorithm, and 3) a table that stores solutions to the subproblems.arrow_forward
- Show that this version of the choice problem is NP-complete; Does the graph G have a spanning tree in which the biggest cost paid by any point is less than the goal cost c?arrow_forwardIn every instance (i.e., example) of the TSP, we are given n cities, where each pair of cities is connected by a weighted edge that measures the cost of traveling between those two cities. Our goal is to find the optimal TSP tour, minimizing the total cost of a Hamiltonian cycle in G. Although it is NP-complete to solve the TSP, there is a simple 2-approximation achieved by first generating a minimum-weight spanning tree of G and using this output to determine our TSP tour. Prove that our output is guaranteed to be a 2-approximation, provided the Triangle Inequality holds. In other words, if OPT is the total cost of the optimal solution, and APP is the total cost of our approximate solution, clearly explain why APP≤ 2∗OPT.arrow_forwardLet NE NFA = {N| N is an nfa and L(N) = Ø} 1. Show the NENFA is in NP 2.Show that NENFA is in Parrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
Operations Research : Applications and Algorithms
Computer Science
ISBN:9780534380588
Author:Wayne L. Winston
Publisher:Brooks Cole