Related questions
Please answer the following question in full detail. Please be specifix about everything:
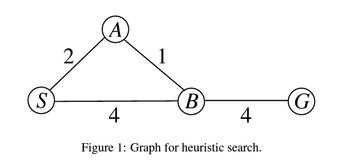
You have learned before that A∗ using graph search is optimal if h(n) is consistent. Does this optimality still hold if h(n) is admissible but inconsistent? Using the graph in Figure 1, let us now show that A∗ using graph search returns the non-optimal solution path (S,B,G) from start node S to goal node G with an admissible but inconsistent h(n). We assume that h(G) = 0. Give nonnegative integer values for h(A) and h(B) such that A∗ using graph search returns the non-optimal solution path (S,B,G) from S to G with an admissible but inconsistent h(n), and tie-breaking is not needed in A∗.
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps
I meant to say that S -> A -> B -> G is the actual optimal path with cost 7 compared to S -> B -> G which has a path cost of 8. But with the heuristics considered this would be the search:
S -> A = 2 + h(A) = 3
S -> B = 4 + h(B) = 7
From there on, it would lead to S -> A -> B -> G and not S -> B -> G, which is we want to have in this problem. So how is this solved? Since S -> A -> G isn't optimal as it is not possible to reach G without intercepting B.
Sorry for the typo earlier.
Isn't the actual optimal S->B->G. If yes, then how are the assumed heuristics valid?
I meant to say that S -> A -> B -> G is the actual optimal path with cost 7 compared to S -> B -> G which has a path cost of 8. But with the heuristics considered this would be the search:
S -> A = 2 + h(A) = 3
S -> B = 4 + h(B) = 7
From there on, it would lead to S -> A -> B -> G and not S -> B -> G, which is we want to have in this problem. So how is this solved? Since S -> A -> G isn't optimal as it is not possible to reach G without intercepting B.
Sorry for the typo earlier.
Isn't the actual optimal S->B->G. If yes, then how are the assumed heuristics valid?
- Please show written work with answer!! An independent set in a graph is a set of vertices no two of which are adjacent to each other. A clique is a complete subgraph of a given graph. This means that there is an edge between any two nodes in the subgraph. The maximal clique is the complete subgraph of a given graph which contains the maximum number of nodes. We know that independent set is a NP complete problem. Transform the independent set to max clique (in polynomial time) to show that Max Clique is also NParrow_forwardQuestion 7. We have computed the shortest path between all the nodes in a weighted graph. Then all the edges increase their costs by adding the same value c > 0. Will the shortest paths change? If your answer is NO, prove so, if the answer is YES, give an example of a graph where at least one shortest path changes.arrow_forwardShow that the decision problem version is an NP-complete problem; Exists, given a graph G and a goal cost c, a spanning tree in which the most any vertex pays is not more than c?arrow_forward
- Consider a graph G that is comprised only of non-negative weight edges such that (u, v) € E, w(u, w) > 0. Is it possible for Bellman-Ford and Dijkstra's algorithm to produce different shortest path trees despite always producing the same shortest-path weights? Justify your answer.arrow_forwardConsider a directed graph G=(V,E) with n vertices, m edges, a starting vertex s∈V, real-valued edge lengths, and no negative cycles. Suppose you know that every shortest path in G from s to another vertex has at most k edges. How quickly can you solve the single-source shortest path problem? (Choose the strongest statement that is guaranteed to be true.) a) O(m+n) b) O(kn) c) O( km) d) O(mn)arrow_forwardWe know that if the heuristic function in A* is good enough, then A* can always find a shortest weighted path between two vertices, and is generally much faster than Dijkstra. Assume we are using a graph where a good heuristic function is well defined for A*, such that A* can always find the same shortest paths as Dijkstra. Briefly explain when you should choose Dijkstra over A* in this case.arrow_forward
- Database System ConceptsComputer ScienceISBN:9780078022159Author:Abraham Silberschatz Professor, Henry F. Korth, S. SudarshanPublisher:McGraw-Hill Education
Starting Out with Python (4th Edition)Computer ScienceISBN:9780134444321Author:Tony GaddisPublisher:PEARSON
Digital Fundamentals (11th Edition)Computer ScienceISBN:9780132737968Author:Thomas L. FloydPublisher:PEARSON 
C How to Program (8th Edition)Computer ScienceISBN:9780133976892Author:Paul J. Deitel, Harvey DeitelPublisher:PEARSON
Database Systems: Design, Implementation, & Manag...Computer ScienceISBN:9781337627900Author:Carlos Coronel, Steven MorrisPublisher:Cengage Learning
Programmable Logic ControllersComputer ScienceISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education