
McDougal Littell Jurgensen Geometry: Student Edition Geometry
5th Edition
ISBN: 9780395977279
Author: Ray C. Jurgensen, Richard G. Brown, John W. Jurgensen
Publisher: Houghton Mifflin Company College Division
expand_more
expand_more
format_list_bulleted
Question
Chapter 11, Problem 26CUR
To determine
To Find: Ratio in which the altitude to hypotenuse divides the hypotenuse.
Expert Solution & Answer
Answer to Problem 26CUR
1:3
Explanation of Solution
Given:
A
Formula used:
Referring to the below figure as per given dimensions:
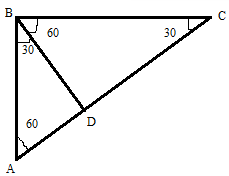
Let
In
In
Dividing (1) by (2):
Chapter 11 Solutions
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Ch. 11.1 - Prob. 1CECh. 11.1 - Prob. 2CECh. 11.1 - Prob. 3CECh. 11.1 - Prob. 4CECh. 11.1 - Prob. 5CECh. 11.1 - Prob. 6CECh. 11.1 - Prob. 7CECh. 11.1 - Prob. 8CECh. 11.1 - Prob. 9CECh. 11.1 - Prob. 10CE
Ch. 11.1 - Prob. 11CECh. 11.1 - Prob. 12CECh. 11.1 - Prob. 13CECh. 11.1 - Prob. 14CECh. 11.1 - Prob. 15CECh. 11.1 - Prob. 1WECh. 11.1 - Prob. 2WECh. 11.1 - Prob. 3WECh. 11.1 - Prob. 4WECh. 11.1 - Prob. 5WECh. 11.1 - Prob. 6WECh. 11.1 - Prob. 7WECh. 11.1 - Prob. 8WECh. 11.1 - Prob. 9WECh. 11.1 - Prob. 10WECh. 11.1 - Prob. 11WECh. 11.1 - Prob. 12WECh. 11.1 - Prob. 13WECh. 11.1 - Prob. 14WECh. 11.1 - Prob. 15WECh. 11.1 - Prob. 16WECh. 11.1 - Prob. 17WECh. 11.1 - Prob. 18WECh. 11.1 - Prob. 19WECh. 11.1 - Prob. 20WECh. 11.1 - Prob. 21WECh. 11.1 - Prob. 22WECh. 11.1 - Prob. 23WECh. 11.1 - Prob. 24WECh. 11.1 - Prob. 25WECh. 11.1 - Prob. 26WECh. 11.1 - Prob. 27WECh. 11.1 - Prob. 28WECh. 11.1 - Prob. 29WECh. 11.1 - Prob. 30WECh. 11.1 - Prob. 31WECh. 11.1 - Prob. 32WECh. 11.1 - Prob. 33WECh. 11.1 - Prob. 34WECh. 11.1 - Prob. 35WECh. 11.1 - Prob. 36WECh. 11.1 - Prob. 37WECh. 11.1 - Prob. 1ECh. 11.1 - Prob. 2ECh. 11.1 - Prob. 3ECh. 11.2 - Prob. 1CECh. 11.2 - Prob. 2CECh. 11.2 - Prob. 3CECh. 11.2 - Prob. 4CECh. 11.2 - Prob. 5CECh. 11.2 - Prob. 6CECh. 11.2 - Prob. 7CECh. 11.2 - Prob. 8CECh. 11.2 - Prob. 9CECh. 11.2 - Prob. 1WECh. 11.2 - Prob. 2WECh. 11.2 - Prob. 3WECh. 11.2 - Prob. 4WECh. 11.2 - Prob. 5WECh. 11.2 - Prob. 6WECh. 11.2 - Prob. 7WECh. 11.2 - Prob. 8WECh. 11.2 - Prob. 9WECh. 11.2 - Prob. 10WECh. 11.2 - Prob. 11WECh. 11.2 - Prob. 12WECh. 11.2 - Prob. 13WECh. 11.2 - Prob. 14WECh. 11.2 - Prob. 15WECh. 11.2 - Prob. 16WECh. 11.2 - Prob. 17WECh. 11.2 - Prob. 18WECh. 11.2 - Prob. 19WECh. 11.2 - Prob. 20WECh. 11.2 - Prob. 21WECh. 11.2 - Prob. 22WECh. 11.2 - Prob. 23WECh. 11.2 - Prob. 24WECh. 11.2 - Prob. 25WECh. 11.2 - Prob. 26WECh. 11.2 - Prob. 27WECh. 11.2 - Prob. 28WECh. 11.2 - Prob. 29WECh. 11.2 - Prob. 30WECh. 11.2 - Prob. 31WECh. 11.2 - Prob. 32WECh. 11.2 - Prob. 33WECh. 11.2 - Prob. 34WECh. 11.2 - Prob. 35WECh. 11.2 - Prob. 36WECh. 11.2 - Prob. 37WECh. 11.2 - Prob. 38WECh. 11.2 - Prob. 39WECh. 11.2 - Prob. 40WECh. 11.2 - Prob. 41WECh. 11.2 - Prob. 42WECh. 11.2 - Prob. 1ECh. 11.2 - Prob. 2ECh. 11.2 - Prob. 3ECh. 11.2 - Prob. 4ECh. 11.2 - Prob. 5ECh. 11.2 - Prob. 6ECh. 11.2 - Prob. 7ECh. 11.2 - Prob. 8ECh. 11.2 - Prob. 9ECh. 11.2 - Prob. 10ECh. 11.2 - Prob. 11ECh. 11.2 - Prob. 12ECh. 11.2 - Prob. 13ECh. 11.2 - Prob. 14ECh. 11.3 - Prob. 1CECh. 11.3 - Prob. 2CECh. 11.3 - Prob. 3CECh. 11.3 - Prob. 4CECh. 11.3 - Prob. 5CECh. 11.3 - Prob. 6CECh. 11.3 - Prob. 7CECh. 11.3 - Prob. 8CECh. 11.3 - Prob. 9CECh. 11.3 - Prob. 10CECh. 11.3 - Prob. 1WECh. 11.3 - Prob. 2WECh. 11.3 - Prob. 3WECh. 11.3 - Prob. 4WECh. 11.3 - Prob. 5WECh. 11.3 - Prob. 6WECh. 11.3 - Prob. 7WECh. 11.3 - Prob. 8WECh. 11.3 - Prob. 9WECh. 11.3 - Prob. 10WECh. 11.3 - Prob. 11WECh. 11.3 - Prob. 12WECh. 11.3 - Prob. 13WECh. 11.3 - Prob. 14WECh. 11.3 - Prob. 15WECh. 11.3 - Prob. 16WECh. 11.3 - Prob. 17WECh. 11.3 - Prob. 18WECh. 11.3 - Prob. 19WECh. 11.3 - Prob. 20WECh. 11.3 - Prob. 21WECh. 11.3 - Prob. 22WECh. 11.3 - Prob. 23WECh. 11.3 - Prob. 24WECh. 11.3 - Prob. 25WECh. 11.3 - Prob. 26WECh. 11.3 - Prob. 27WECh. 11.3 - Prob. 28WECh. 11.3 - Prob. 29WECh. 11.3 - Prob. 30WECh. 11.3 - Prob. 31WECh. 11.3 - Prob. 32WECh. 11.3 - Prob. 33WECh. 11.3 - Prob. 34WECh. 11.3 - Prob. 1ECh. 11.3 - Prob. 2ECh. 11.3 - Prob. 3ECh. 11.3 - Prob. 1MRECh. 11.3 - Prob. 2MRECh. 11.3 - Prob. 3MRECh. 11.3 - Prob. 4MRECh. 11.3 - Prob. 5MRECh. 11.3 - Prob. 6MRECh. 11.3 - Prob. 7MRECh. 11.3 - Prob. 8MRECh. 11.4 - Prob. 1CECh. 11.4 - Prob. 2CECh. 11.4 - Prob. 3CECh. 11.4 - Prob. 4CECh. 11.4 - Prob. 5CECh. 11.4 - Prob. 6CECh. 11.4 - Prob. 7CECh. 11.4 - Prob. 8CECh. 11.4 - Prob. 9CECh. 11.4 - Prob. 1WECh. 11.4 - Prob. 2WECh. 11.4 - Prob. 3WECh. 11.4 - Prob. 4WECh. 11.4 - Prob. 5WECh. 11.4 - Prob. 6WECh. 11.4 - Prob. 7WECh. 11.4 - Prob. 8WECh. 11.4 - Prob. 9WECh. 11.4 - Prob. 10WECh. 11.4 - Prob. 11WECh. 11.4 - Prob. 12WECh. 11.4 - Prob. 13WECh. 11.4 - Prob. 14WECh. 11.4 - Prob. 15WECh. 11.4 - Prob. 16WECh. 11.4 - Prob. 17WECh. 11.4 - Prob. 18WECh. 11.4 - Prob. 19WECh. 11.4 - Prob. 20WECh. 11.4 - Prob. 21WECh. 11.4 - Prob. 22WECh. 11.4 - Prob. 1ST1Ch. 11.4 - Prob. 2ST1Ch. 11.4 - Prob. 3ST1Ch. 11.4 - Prob. 4ST1Ch. 11.4 - Prob. 5ST1Ch. 11.4 - Prob. 6ST1Ch. 11.4 - Prob. 7ST1Ch. 11.4 - Prob. 8ST1Ch. 11.4 - Prob. 9ST1Ch. 11.4 - Prob. 10ST1Ch. 11.4 - Prob. 1ECh. 11.4 - Prob. 2ECh. 11.5 - Prob. 1CECh. 11.5 - Prob. 2CECh. 11.5 - Prob. 3CECh. 11.5 - Prob. 4CECh. 11.5 - Prob. 5CECh. 11.5 - Prob. 6CECh. 11.5 - Prob. 7CECh. 11.5 - Prob. 8CECh. 11.5 - Prob. 9CECh. 11.5 - Prob. 10CECh. 11.5 - Prob. 11CECh. 11.5 - Prob. 12CECh. 11.5 - Prob. 13CECh. 11.5 - Prob. 14CECh. 11.5 - Prob. 1WECh. 11.5 - Prob. 2WECh. 11.5 - Prob. 3WECh. 11.5 - Prob. 4WECh. 11.5 - Prob. 5WECh. 11.5 - Prob. 6WECh. 11.5 - Prob. 7WECh. 11.5 - Prob. 8WECh. 11.5 - Prob. 9WECh. 11.5 - Prob. 10WECh. 11.5 - Prob. 11WECh. 11.5 - Prob. 12WECh. 11.5 - Prob. 13WECh. 11.5 - Prob. 14WECh. 11.5 - Prob. 15WECh. 11.5 - Prob. 16WECh. 11.5 - Prob. 17WECh. 11.5 - Prob. 18WECh. 11.5 - Prob. 19WECh. 11.5 - Prob. 20WECh. 11.5 - Prob. 21WECh. 11.5 - Prob. 22WECh. 11.5 - Prob. 23WECh. 11.5 - Prob. 24WECh. 11.5 - Prob. 25WECh. 11.5 - Prob. 26WECh. 11.5 - Prob. 27WECh. 11.5 - Prob. 28WECh. 11.5 - Prob. 29WECh. 11.5 - Prob. 30WECh. 11.5 - Prob. 31WECh. 11.5 - Prob. 32WECh. 11.5 - Prob. 33WECh. 11.5 - Prob. 34WECh. 11.5 - Prob. 35WECh. 11.5 - Prob. 1ECh. 11.5 - Prob. 2ECh. 11.5 - Prob. 3ECh. 11.5 - Prob. 4ECh. 11.5 - Prob. 1ARCh. 11.5 - Prob. 2ARCh. 11.5 - Prob. 3ARCh. 11.5 - Prob. 4ARCh. 11.5 - Prob. 5ARCh. 11.5 - Prob. 6ARCh. 11.5 - Prob. 7ARCh. 11.5 - Prob. 8ARCh. 11.6 - Prob. 1CECh. 11.6 - Prob. 2CECh. 11.6 - Prob. 3CECh. 11.6 - Prob. 4CECh. 11.6 - Prob. 5CECh. 11.6 - Prob. 6CECh. 11.6 - Prob. 7CECh. 11.6 - Prob. 1WECh. 11.6 - Prob. 2WECh. 11.6 - Prob. 3WECh. 11.6 - Prob. 4WECh. 11.6 - Prob. 5WECh. 11.6 - Prob. 6WECh. 11.6 - Prob. 7WECh. 11.6 - Prob. 8WECh. 11.6 - Prob. 9WECh. 11.6 - Prob. 10WECh. 11.6 - Prob. 11WECh. 11.6 - Prob. 12WECh. 11.6 - Prob. 13WECh. 11.6 - Prob. 14WECh. 11.6 - Prob. 15WECh. 11.6 - Prob. 16WECh. 11.6 - Prob. 17WECh. 11.6 - Prob. 18WECh. 11.6 - Prob. 19WECh. 11.6 - Prob. 20WECh. 11.6 - Prob. 21WECh. 11.6 - Prob. 22WECh. 11.6 - Prob. 23WECh. 11.6 - Prob. 24WECh. 11.6 - Prob. 25WECh. 11.6 - Prob. 26WECh. 11.6 - Prob. 27WECh. 11.6 - Prob. 28WECh. 11.6 - Prob. 29WECh. 11.6 - Prob. 30WECh. 11.7 - Prob. 1CECh. 11.7 - Prob. 2CECh. 11.7 - Prob. 3CECh. 11.7 - Prob. 4CECh. 11.7 - Prob. 5CECh. 11.7 - Prob. 6CECh. 11.7 - Prob. 7CECh. 11.7 - Prob. 8CECh. 11.7 - Prob. 9CECh. 11.7 - Prob. 10CECh. 11.7 - Prob. 11CECh. 11.7 - Prob. 12CECh. 11.7 - Prob. 13CECh. 11.7 - Prob. 14CECh. 11.7 - Prob. 15CECh. 11.7 - Prob. 1WECh. 11.7 - Prob. 2WECh. 11.7 - Prob. 3WECh. 11.7 - Prob. 4WECh. 11.7 - Prob. 5WECh. 11.7 - Prob. 6WECh. 11.7 - Prob. 7WECh. 11.7 - Prob. 8WECh. 11.7 - Prob. 9WECh. 11.7 - Prob. 10WECh. 11.7 - Prob. 11WECh. 11.7 - Prob. 12WECh. 11.7 - Prob. 13WECh. 11.7 - Prob. 14WECh. 11.7 - Prob. 15WECh. 11.7 - Prob. 16WECh. 11.7 - Prob. 17WECh. 11.7 - Prob. 18WECh. 11.7 - Prob. 19WECh. 11.7 - Prob. 20WECh. 11.7 - Prob. 21WECh. 11.7 - Prob. 22WECh. 11.7 - Prob. 23WECh. 11.7 - Prob. 24WECh. 11.7 - Prob. 25WECh. 11.7 - Prob. 26WECh. 11.7 - Prob. 27WECh. 11.7 - Prob. 28WECh. 11.7 - Prob. 29WECh. 11.7 - Prob. 30WECh. 11.7 - Prob. 31WECh. 11.7 - Prob. 32WECh. 11.8 - Prob. 1CECh. 11.8 - Prob. 2CECh. 11.8 - Prob. 3CECh. 11.8 - Prob. 4CECh. 11.8 - Prob. 1WECh. 11.8 - Prob. 2WECh. 11.8 - Prob. 3WECh. 11.8 - Prob. 4WECh. 11.8 - Prob. 5WECh. 11.8 - Prob. 6WECh. 11.8 - Prob. 7WECh. 11.8 - Prob. 8WECh. 11.8 - Prob. 9WECh. 11.8 - Prob. 10WECh. 11.8 - Prob. 11WECh. 11.8 - Prob. 12WECh. 11.8 - Prob. 13WECh. 11.8 - Prob. 14WECh. 11.8 - Prob. 15WECh. 11.8 - Prob. 16WECh. 11.8 - Prob. 17WECh. 11.8 - Prob. 1ST2Ch. 11.8 - Prob. 2ST2Ch. 11.8 - Prob. 3ST2Ch. 11.8 - Prob. 4ST2Ch. 11.8 - Prob. 5ST2Ch. 11.8 - Prob. 6ST2Ch. 11.8 - Prob. 7ST2Ch. 11.8 - Prob. 8ST2Ch. 11.8 - Prob. 9ST2Ch. 11.8 - Prob. 10ST2Ch. 11.8 - Prob. 1AECh. 11.8 - Prob. 2AECh. 11.8 - Prob. 3AECh. 11.8 - Prob. 4AECh. 11.8 - Prob. 5AECh. 11.8 - Prob. 6AECh. 11.8 - Prob. 7AECh. 11.8 - Prob. 8AECh. 11.8 - Prob. 1BECh. 11.8 - Prob. 2BECh. 11.8 - Prob. 3BECh. 11.8 - Prob. 4BECh. 11 - Prob. 1CRCh. 11 - Prob. 2CRCh. 11 - Prob. 3CRCh. 11 - Prob. 4CRCh. 11 - Prob. 5CRCh. 11 - Prob. 6CRCh. 11 - Prob. 7CRCh. 11 - Prob. 8CRCh. 11 - Prob. 9CRCh. 11 - Prob. 10CRCh. 11 - Prob. 11CRCh. 11 - Prob. 12CRCh. 11 - Prob. 13CRCh. 11 - Prob. 14CRCh. 11 - Prob. 15CRCh. 11 - Prob. 16CRCh. 11 - Prob. 17CRCh. 11 - Prob. 18CRCh. 11 - Prob. 19CRCh. 11 - Prob. 20CRCh. 11 - Prob. 21CRCh. 11 - Prob. 22CRCh. 11 - Prob. 23CRCh. 11 - Prob. 1CTCh. 11 - Prob. 2CTCh. 11 - Prob. 3CTCh. 11 - Prob. 4CTCh. 11 - Prob. 5CTCh. 11 - Prob. 6CTCh. 11 - Prob. 7CTCh. 11 - Prob. 8CTCh. 11 - Prob. 9CTCh. 11 - Prob. 10CTCh. 11 - Prob. 11CTCh. 11 - Prob. 12CTCh. 11 - Prob. 13CTCh. 11 - Prob. 14CTCh. 11 - Prob. 15CTCh. 11 - Prob. 16CTCh. 11 - Prob. 17CTCh. 11 - Prob. 18CTCh. 11 - Prob. 19CTCh. 11 - Prob. 20CTCh. 11 - Prob. 1CURCh. 11 - Prob. 2CURCh. 11 - Prob. 3CURCh. 11 - Prob. 4CURCh. 11 - Prob. 5CURCh. 11 - Prob. 6CURCh. 11 - Prob. 7CURCh. 11 - Prob. 8CURCh. 11 - Prob. 9CURCh. 11 - Prob. 10CURCh. 11 - Prob. 11CURCh. 11 - Prob. 12CURCh. 11 - Prob. 13CURCh. 11 - Prob. 14CURCh. 11 - Prob. 15CURCh. 11 - Prob. 16CURCh. 11 - Prob. 17CURCh. 11 - Prob. 18CURCh. 11 - Prob. 19CURCh. 11 - Prob. 20CURCh. 11 - Prob. 21CURCh. 11 - Prob. 22CURCh. 11 - Prob. 23CURCh. 11 - Prob. 24CURCh. 11 - Prob. 25CURCh. 11 - Prob. 26CURCh. 11 - Prob. 27CURCh. 11 - Prob. 28CURCh. 11 - Prob. 29CURCh. 11 - Prob. 30CURCh. 11 - Prob. 31CURCh. 11 - Prob. 32CURCh. 11 - Prob. 33CURCh. 11 - Prob. 34CURCh. 11 - Prob. 35CURCh. 11 - Prob. 36CURCh. 11 - Prob. 37CUR
Additional Math Textbook Solutions
Find more solutions based on key concepts
Choose your test Use the test of your choice to determine whether the following series converge. 49. k=31lnk
Calculus: Early Transcendentals (2nd Edition)
If n is a counting number, bn, read______, indicates that there are n factors of b. The number b is called the_...
Algebra and Trigonometry (6th Edition)
Confidence Intervals. In Exercises 9–24, construct the confidence interval estimate of the mean.
16. Arsenic in...
Elementary Statistics (13th Edition)
Stating the Null and Alternative Hypotheses In Exercises 25–30, write the claim as a mathematical statement. St...
Elementary Statistics: Picturing the World (7th Edition)
Drug for Nausea Ondansetron (Zofran) is a drug used by some pregnant women for nausea. There was some concern t...
Introductory Statistics
the below subtraction
Pre-Algebra Student Edition
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- 3. Construct a triangle in the Poincare plane with all sides equal to ln(2). (Hint: Use the fact that, the circle with center (0,a) and radius ln(r), r>1 in the Poincaré plane is equal to the point set { (x,y) : x^2+(y-1/2(r+1/r)a)^2=1/4(r-1/r)^2a^2 }arrow_forwardn. g. = neutral geometry <ABC = angle ABC \leq = less or equal than sqrt{x} = square root of x cLr = the line in the Poincaré plane defined by the equation (x-c)^2+y^2=r^2 1. Find the bisector of the angle <ABC in the Poincaré plane, where A=(0,5), B=(0,3) and C=(2,\sqrt{21})arrow_forward2. Let l=2L\sqrt{5} and P=(1,2) in the Poincaré plane. Find the uniqe line l' through P such that l' is orthogonal to l.arrow_forward
- Let A, B and C be three points in neutral geometry, lying on a circle with center D. If D is in the interior of the triangle ABC, then show that m(<ABC) \leq 1/2m(<ADC).arrow_forwardиз Review the deck below and determine its total square footage (add its deck and backsplash square footage together to get the result). Type your answer in the entry box and click Submit. 126 1/2" 5" backsplash A 158" CL 79" B 26" Type your answer here.arrow_forwardIn the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forward
- Select all that apply. 104 8 6 4 2 U U' -10 -8 -6 4 -2 2 4 6 10 -2 V' W' -4 -6 -8 -10 W V Select 2 correct answerts! The side lengths are equal in measure. The scale factor is 1/5. The figure has been enlarged in size. The center of dilation is (0.0) 8 10 Xarrow_forwardIn the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forwardQll consider the problem -abu+bou+cu=f., u=0 ondor I prove atu, ul conts. @ if Blu,v) = (b. 14, U) + ((4,0) prove that B244) = ((c- — ob)4;4) ③if c±vbo prove that acuius v. elliptic.arrow_forward
- Q3: Define the linear functional J: H₁(2) R by ¡(v) = a(v, v) - L(v) Л Let u be the unique weak solution to a(u,v) = L(v) in H(2) and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u) can be rewritten under 1(u) = u Au-ub, algebraic form 1 2 Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer 1- show that the solution to -Au = f in A, u = 0 on a satisfies the stability Vullfll and show that ||V(u u)||||||2 - ||vu||2 2- Prove that Where lu-ul Chuz - !ull = a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinea forta Л a(u, v) = (Au, Av) (Vu, Vv + (Vu, v) + (u,v) Show that a(u, v) continues and V- elliptic on H(2)arrow_forward7) In the diagram below of quadrilateral ABCD, E and F are points on AB and CD respectively, BE=DF, and AE = CF. Which conclusion can be proven? A 1) ED = FB 2) AB CD 3) ZA = ZC 4) ZAED/CFB E B D 0arrow_forward1) In parallelogram EFGH, diagonals EG and FH intersect at point I such that EI = 2x - 2 and EG = 3x + 11. Which of the following is the length of GH? a) 15 b) 28 c) 32 d) 56arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Algebra - Pythagorean Theorem; Author: yaymath;https://www.youtube.com/watch?v=D_y_owf1WsI;License: Standard YouTube License, CC-BY
The Organic Chemistry Tutor; Author: Pythagorean Theorem Explained!;https://www.youtube.com/watch?v=B0G35RkmwSw;License: Standard Youtube License