Fox and McDonald's Introduction to Fluid Mechanics
9th Edition
ISBN: 9781118912652
Author: Philip J. Pritchard, John W. Mitchell
Publisher: WILEY
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 7, Problem 32P
The sketch shows an air jet discharging vertically. Experiments show that a ball placed in the jet is suspended in a stable position. The equilibrium height of the ball in the jet is found to depend on D, d, V, ρ, μ, and W, where W is the weight of the ball. Dimensional analysis is suggested to correlate experimental data. Find the Π parameters that characterize this phenomenon.
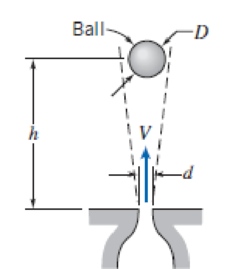
P7.32
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
1. (a)
The motion of a floating vessel through the surrounding fluid results in
a drag force D which is thought to depend upon the vessel's speed v,
its length I, the density p and dynamic viscosity μ of the fluid and the
acceleration due to gravity g.
Show that:-
D = pv²1² (1)
(b)
In order to predict the drag on a full scale 50m long ship traveling at
7m/s in sea water at 5°C of density 1027.7225 kg/m³ and viscosity
1.62 x 103 Pa.s, a model 3m long is tested in a liquid of density
805 kg/m³.
What speed does the model need to be tested at and what is the
required viscosity of the liquid?
1. The thrust of a marine propeller Fr depends on water density p, propeller diameter D, speed of advance
through the water V, acceleration due to gravity g, the angular speed of the propeller w, the water pressure
p, and the water viscosity μ. You want to find a set of dimensionless variables on which the thrust coefficient
depends. In other words
CT =
FT
· = ƒen(#1, #2, ...)
pV2D2
(a) What is k? Explain.
(b) Find the 's on the right-hand-side of equation 1 if one of them HAS to be a Froude number gD/V²,
(1)
The time t d to drain a liquid from a hole in the bottom of atank is a function of the hole diameter d , the initial fluidvolume y 0 , the initial liquid depth h 0 , and the density ρ andviscosity μ of the fluid. Rewrite this relation as a dimensionlessfunction, using Ipsen’s method.
Chapter 7 Solutions
Fox and McDonald's Introduction to Fluid Mechanics
Ch. 7 - The slope of the free surface of a steady wave in...Ch. 7 - One-dimensional unsteady flow in a thin liquid...Ch. 7 - In atmospheric studies the motion of the earths...Ch. 7 - Fluid fills the space between two parallel plates....Ch. 7 - By using order of magnitude analysis, the...Ch. 7 - Consider a disk of radius R rotating in an...Ch. 7 - An unsteady, two-dimensional, compressible,...Ch. 7 - Experiments show that the pressure drop for flow...Ch. 7 - At very low speeds, the drag on an object is...Ch. 7 - We saw in Chapter 3 that the buoyant force, FB, on...
Ch. 7 - Assume that the velocity acquired by a body...Ch. 7 - Derive by dimensional analysis an expression for...Ch. 7 - The speed of shallow water waves in the ocean...Ch. 7 - The speed, V, of a free-surface wave in shallow...Ch. 7 - The boundary-layer thickness, , on a smooth flat...Ch. 7 - The speed, V, of a free-surface gravity wave in...Ch. 7 - Derive an expression for the velocity of very...Ch. 7 - Derive an expression for the axial thrust exerted...Ch. 7 - Derive an expression for drag force on a smooth...Ch. 7 - The energy released during an explosion, E, is a...Ch. 7 - Measurements of the liquid height upstream from an...Ch. 7 - The load-carrying capacity, W, of a journal...Ch. 7 - Derive an expression for the drag force on a...Ch. 7 - A circular disk of diameter d and of negligible...Ch. 7 - Two cylinders are concentric, the outer one fixed...Ch. 7 - The time, t, for oil to drain out of a viscosity...Ch. 7 - You are asked to find a set of dimensionless...Ch. 7 - A continuous belt moving vertically through a bath...Ch. 7 - Derive an expression for the frictional torque...Ch. 7 - Tests on the established flow of six different...Ch. 7 - The power, P, required to drive a fan is believed...Ch. 7 - The sketch shows an air jet discharging...Ch. 7 - The diameter, d, of bubbles produced by a...Ch. 7 - Choked-flow nozzles are often used to meter the...Ch. 7 - A large tank of liquid under pressure is drained...Ch. 7 - Spin plays an important role in the flight...Ch. 7 - The power loss, P, in a journal bearing depends on...Ch. 7 - The thrust of a marine propeller is to be measured...Ch. 7 - The rate dT/dt at which the temperature T at the...Ch. 7 - When a valve is closed suddenly in a pipe with...Ch. 7 - An airship is to operate at 20 m/s in air at...Ch. 7 - An airplane wing of 3 m chord length moves through...Ch. 7 - A flat plate 1.5 m long and 0.3 m wide is towed at...Ch. 7 - This 1:12 pump model using water at 15C simulates...Ch. 7 - An ocean-going vessel is to be powered by a...Ch. 7 - On a cruise ship, passengers complain about the...Ch. 7 - A 1:3 scale model of a torpedo is tested in a wind...Ch. 7 - A flow rate of 0:18 m3/s of water at 20C...Ch. 7 - A force of 9 N is required to tow a 1:50 ship...Ch. 7 - An airplane wing, with chord length of 1.5 m and...Ch. 7 - A water pump with impeller diameter of 24 in. is...Ch. 7 - A model hydrofoil is to be tested at 1:20 scale....Ch. 7 - A ship 120 m long moves through freshwater at 15C...Ch. 7 - A 1:30 scale model of a cavitating overflow...Ch. 7 - In some speed ranges, vortices are shed from the...Ch. 7 - A 1:8 scale model of a tractor-trailer rig is...Ch. 7 - On a cruise ship, passengers complain about the...Ch. 7 - When a sphere of 0.25 mm diameter and specific...Ch. 7 - The flow about a 150 mm artillery projectile which...Ch. 7 - Your favorite professor likes mountain climbing,...Ch. 7 - A 1:50-scale model of a submarine is to be tested...Ch. 7 - Consider water flow around a circular cylinder, of...Ch. 7 - A 1:10 scale model of a tractor-trailer rig is...Ch. 7 - The power, P, required to drive a fan is assumed...Ch. 7 - Over a certain range of air speeds, V, the lift,...Ch. 7 - The pressure rise, p, of a liquid flowing steadily...Ch. 7 - An axial-flow pump is required to deliver 0.75...Ch. 7 - A model propeller 1 m in diameter is tested in a...Ch. 7 - Consider Problem 7.38. Experience shows that for...Ch. 7 - Closed-circuit wind tunnels can produce higher...Ch. 7 - A 1:16 model of a bus is tested in a wind tunnel...Ch. 7 - The propagation speed of small-amplitude surface...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
In a math expression, multiplication and division take place before addition and subtraction.
Starting Out with Programming Logic and Design (5th Edition) (What's New in Computer Science)
What is a storyboard?
Computer Science: An Overview (13th Edition) (What's New in Computer Science)
A loading causes the member to deform into the dashed shape. Explain how to determine the normal strains CD and...
Mechanics of Materials (10th Edition)
ICA 8-38
An ideal gas is kept in a 10-liter [L] container at a pressure of 1.5 atmospheres [atm] and a temperat...
Thinking Like an Engineer: An Active Learning Approach (4th Edition)
Explain what must be done when fully replicating a database but allowing only one computer to process updates.
Database Concepts (8th Edition)
What function or functions are performed by the outer zone of the welding flame?
Degarmo's Materials And Processes In Manufacturing
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- When a sphere falls freely through a homogeneous fluid, it reaches a terminal velocity at which the weight of the sphere is balanced by the buoyant force and the frictional resistance of the fluid. Make a dimensional analysis of this problem and indicate how experimental data for this problem could be correlated. Neglect compressibility effects and the influence of surface roughness.arrow_forwardA simply supported beam of diameter D , length L , and modulusof elasticity E is subjected to a fluid crossflow of velocityV , density ρ , and viscosity μ . Its center deflection δ isassumed to be a function of all these variables. ( a ) Rewritethis proposed function in dimensionless form. ( b ) Suppose itis known that δ is independent of μ , inversely proportionalto E , and dependent only on ρ V 2 , not ρ and V separately.Simplify the dimensionless function accordingly. Hint:Take L , ρ , and V as r e peating variables.arrow_forwardA liquid of density ? and viscosity ? is pumped at volume flow rate V· through a pump of diameter D. The blades of the pump rotate at angular velocity ? . The pump supplies a pressure rise ΔP to the liquid. Using dimensional analysis, generate a dimensionless relationship for ΔP as a function of the other parameters in the problem. Identify any established nondimensional parameters that appear in your result. Hint: For consistency (and whenever possible), it is wise to choose a length, a density, and a velocity (or angular velocity) as repeating variables.arrow_forward
- Problem 4: The power P developed by a wind turbine is a function of diameter D, air density p, wind speed V, and rotational rate @. Viscous effect is negligible. (4a) Rewrite the above relationship in a dimensionless form; (4b) In a wind tunnel, a small model with a diameter of 90cm, rotating at 1200 RPM (revolution per minute), delivered 200 watts when the wind speed is 12m/s. The data are to be used for a prototype of diameter of 50m and wind speed of 8 m/s. For dynamic similarity, what will be (i) the rotational speed of the prototype turbine? (ii) the power delivered by the prototype turbine? Assume air has sea-level density.arrow_forwardWhen a fluid flows slowly past a vertical plate of height h and width b, pressure develops on the face of the plate. Assume that the pressure, p, at the midpoint of the plate is a function of plate height and width, the approach velocity V, and the fluid viscosity u and fluid density p. Make use of dimensional analysis to determine how the pressure, p will be formed with a dimensionless group. (Take b, V. p as repeating variables). Select one: O a. n1 = p /V² p O b. n1 = p/Ve O c.n1 = p/Vp? O d. 11 = p/V² p²arrow_forwardQ1: If an air stream flowing at velocity (U) pasta body of length (L) causes a drag force (F) on the body which depends only upon U, L, and fluid viscosity μ. Formulate the suitable dimensionless parameter of the air drag force.arrow_forward
- The thrust F of a propeller is generally thought to be afunction of its diameter D and angular velocity V , the forwardspeed V , and the density ρ and viscosity μ of the fl uid.Rewrite this relationship as a dimensionless function.arrow_forwardPlease solve this problem, Thank you very much! Figure is attached 1. liquids in rotating cylinders rotates as a rigid body and considered at rest. The elevation difference h between the center of the liquid surface and the rim of the liquid surface is a function of angular velocity ?, fluid density ?, gravitational acceleration ?, and radius ?. Use the method of repeating variables to find a dimensionless relationship between the parameters. Show all the steps.arrow_forwardP1.20 A baseball, with m = 145 g, is thrown directly upward from the initial position z = 0 and Vo = 45 m/s. The air drag on the ball is CV², as in Prob. 1.19, where C~ 0.0013 N: s*/m". Set up a differential equation for the ball motion, and solve for the instantaneous velocity V(t) and position z(1). Find the maximum height zmax reached by the ball, and compare your results with the classical case of zero air drag.arrow_forward
- Problem 01 t* = 0.015s 100 m In 1940, fluid dynamicist G. I. Taylor determined from Dimensional Analysis that the radius R of a fireball created by a nuclear explosion is exclusively determined by the released energy E, initial gas density po and elapsed time t* since detonation. Note: 1 kiloton = 4 × 1012 J (Joules). (a) List in a table the primary dimensions of R, E, po and t*. How many primary dimensions are there? (b) Find the single Pi group that controls the blast radius R. (c) In 1945, an experiment was conducted in the desert of New Mexico with a 20 kiloton bomb. On that day, air density was recorded at po = 1.23kg/m³. The photograph above taken at t* 0.015s shows a radius R108 m. Compute the value of the Pi group you have found. (d) Assuming that the Pi group remains constant, find the blast radius R at t* = 0.02s.arrow_forwardThe drag force on a submarine, which is moving on the surface, is to be determined by a test on a model which is scaled down to one-twentieth of the prototype. The test is to be carried in a towing tank, where the model submarine is moved along a channel of liquid. The density and the kinematic viscosity of the seawater are 1010 kg/m³ and 1.3x10-6 m 2/s, respectively. The speed of the prototype is 2.6 m/s. Assume that F = f(V, L. g. p.), using pi-theorem and similarity principle to: a) Determine the speed at which the model should be moved in the towing tank. b) Determine the kinematic viscosity of the liquid that should be used in the towing tank.arrow_forward(b) A Formula 1 team tests their car in a wind tunnel at a scale of 50%, at a speed of Vwinarunnet = 50 m/s. The measured downforce at this speed is Foownforce.WT = 3000 N and the model reference area is Aref wT = 0.5 m?. 1. Find the downforce magnitude on the full-scale race car at the same Reynolds number. Assume constant air density p = 1.2 kg/m. II. It is said that F1 cars could travel upside down, as shown below. At what speed should the full-scale car travel to achieve this, if its mass is m = 740 kg? The acceleration of gravity is g = 9.81 m/s?. Downforce Weightarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
What is Metrology in Mechanical Engineering? | Terminologies & Measurement; Author: GaugeHow;https://www.youtube.com/watch?v=_KhMhFRehy8;License: Standard YouTube License, CC-BY