
Part (a)
Fraction of its initial energy is lost during the bounce.
Part (a)
Answer to Problem 52P
Solution: 20%
Explanation of Solution
Given:
Initial height of ball =2.0 m
Maximum height attained by ball after bounce =1.6 m
Formula Used: P.E of a body at height from a point (reference point) =mgh
Conservation of mechanical energy.
KE2+PE2=KE1+PE1
When only conservative force is acting.
Calculation:
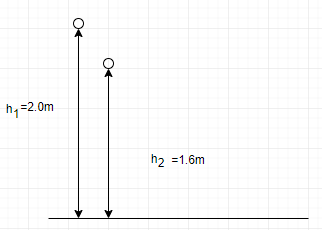
Initial height of ball h1=2.0 m
P.E1=mgh1
Maximum height attained by ball is h2
PE2=mgh2
Loss in P.E (P.E2)=P.E1-P.E2
=mg h1-mg h2=mg(h1-h2).
Fraction of its potential energy losses.
=mg(h1-h2)mg h1×100=h1-h2h1×100=2-1.62×100=0.42×100=20%
Conclusion:The fraction of energy lost during the bounce =20%
Part (b)
The ball’s speed just before and just after the bounce.
Part (b)
Answer to Problem 52P
Solution: 6.3 m/s (just before bounce), 5.6 m/s (just after bounce)
Explanation of Solution
Given: Initial height of ball =2.0 m
Maximum height attained by ball after bounce =1.6 m
Formula Used: P.E of a body at height from a point (reference point) =mgh
Conservation of mechanical energy.
KE2+PE2=KE1+PE1
(when only conservative force is acting)
Calculation:
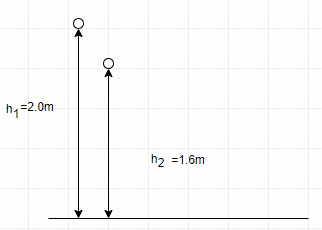
Before and after bounce only gravitational force is acting on ball (conservative force) so apply conservation of energy before bounce and after bounces.
Initial mechanical energy of ball (Ei)
=P.E1+K.E1=mg h1+12m(0)2=mg h1.
Mechanical energy of ball just before collision (Ef)
=P.E2+K.E2=mg(0)+12m(v2)2
Reference position for potential energy is taken ground surface.
Ei=Efmg h1=12m(v2)2v2=√2gh1 =√2×9.80×2 =6.26 m/s≈6.3 m/s
Speed of ball just before bounce =6.26m/s2 after bounce
Initial mechanical energy of ball (Ei)
=P.E1+K.E1=mg(0)+12mv12=12mv12
Final mechanical energy of ball (Ef)
=P.E2+K.E2=mg h2+12m(0)2 (at the heighest point velocity=0)=mg h2
12mv22=mgh2 (conservation of energy)v2=√2gh2 =√2×9.80×1.60 =5.6 m/s.
Conclusion:
Speed of ball just after bounce =5.6 m/s
Part (c)
Where did the energy go
Part (c)
Answer to Problem 52P
Solution:Into heat and sound energy
Explanation of Solution
Loss in mechanical energy is converted into heat and sound energy during collision with Earth’s surface.
Conclusion:
Loss in mechanical energy is converted into sound and heat energy.
Chapter 6 Solutions
Physics: Principles with Applications
Additional Science Textbook Solutions
Campbell Biology (11th Edition)
College Physics: A Strategic Approach (3rd Edition)
Microbiology: An Introduction
Campbell Essential Biology (7th Edition)
Campbell Essential Biology with Physiology (5th Edition)
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
- The rectangular loop of wire shown in the figure (Figure 1) has a mass of 0.18 g per centimeter of length and is pivoted about side ab on a frictionless axis. The current in the wire is 8.5 A in the direction shown. Find the magnitude of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane. The answer is .028 T, I just need help understanding how to do it. Please show all steps.arrow_forwardA ray of light from an object you want to look at strikes a mirror so that the light ray makes a 32 degree angle relative to the normal line (a line perpendicular to the surface of the mirror at the point where the ray strikes the mirror). If you want to see the object in the mirror, what angle does your line of sight need to make relative to the normal line? Give your answer as the number of degrees.arrow_forwardSuppose you have a converging lens with a focal length of 65 cm. You hold this lens 120 cm away from a candle. How far behind the lens should you place a notecard if you want to form a clear image of the candle, on the card? Give your answer as the number of centimeters.arrow_forward
- Suppose you have a diverging lens with a focal length of - 25 cm. You look through this lens at a sleeping squirrel, and notice that it forms a virtual image of the squirrel with di = - 18 cm. How far away from the lens is the squirrel? Give your answer as the number of centimeters (a positive number).arrow_forwardDiamond has an index of refraction of about 2.4. Suppose you cut a diamond so it has a flat surface, and shine a laser pointer beam so that it makes a 27 degree angle with respect to the normal line to that surface. What angle will the laser beam make with respect to the normal after it passes through the air-diamond boundary and is inside the diamond? Give your answer as the number of degrees.arrow_forwardFind current of each line of D,E, and F. Where V1 is 9V, V2 is 7V, R1 is 989 , R2 is 2160, R3 is 4630 , R4 is 5530, R5 is 6720, and E is 16V. Please explain all steps. Thank youarrow_forward
- You are tasked with designing a parallel-plate capacitor using two square metal plates, eachwith an area of 0.5 m², separated by a 0.1 mm thick layer of air. However, to increase the capacitance,you decide to insert a dielectric material with a dielectric constant κ = 3.0 between the plates. Describewhat happens (and why) to the E field between the plates when the dielectric is added in place of theair.arrow_forwardCalculate the work required to assemble a uniform charge Q on a thin spherical shell of radiusR. Start with no charge and add infinitesimal charges dq until the total charge reaches Q, assuming thecharge is always evenly distributed over the shell’s surface. Show all steps.arrow_forwardRod AB is fixed to a smooth collar D, which slides freely along the vertical guide shown in (Figure 1). Point C is located just to the left of the concentrated load P = 70 lb. Suppose that w= 17 lb/ft. Follow the sign convention. Part A Figure 3 ft -1.5 ft √30° 1 of 1 Determine the normal force at point C. Express your answer in pounds to three significant figures. ΜΕ ΑΣΦ Η vec Nc= Submit Request Answer Part B Determine the shear force at point C. Express your answer in pounds to three significant figures. VC= ΜΕ ΑΣΦΗ vec Submit Request Answer Part C Determine the moment at point C. Express your answer in pound-feet to three significant figures. Mc= Ο ΑΣΦ Η vec Submit Request Answer Provide Feedback ? ? lb lb ? lb-ftarrow_forward
- Consider a uniformly charged ring of radius R with total charge Q, centered at the origin inthe xy-plane. Find the electric field (as a vector) at a point on the z-axis at a distance z above thecenter of the ring. Assume the charge density is constant along the ring.arrow_forward3) If the slider block C is moving at 3m/s, determine the angular velocity of BC and the crank AB at the instant shown. (Use equation Vs Vc wx fuc, then use equation Vs VA + Ve/athen write it in terms of w and the appropriate r equate the two and solve) 0.5 m B 1 m 60° A 45° vc = 3 m/sarrow_forward3) If the slider block C is moving at 3m/s, determine the angular velocity of BC and the crank AB at the instant shown. (Use equation Vs Vc wxf, then use equation V, VA + Va/Athen write it in terms of w and the appropriate r equate the two and solve) f-3marrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





