
Concept explainers
Ends A and D of the two solid steel shafts AB and CD are fixed, while ends B and C are connected to gears as shown. Knowing that the allowable shearing stress is 50 MPa in each shaft, determine the largest torque T that can be applied to gear B.
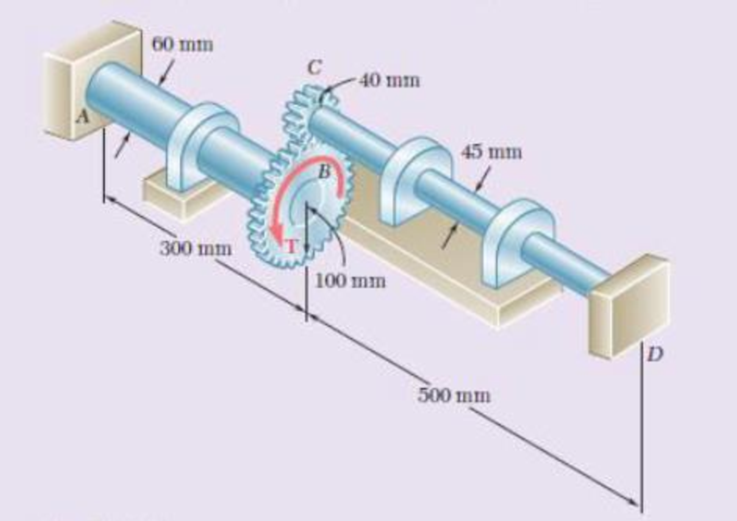
Fig. P3.157
Find the largest torque (T) that can be applied to gear B.
Answer to Problem 157RP
The largest torque (T) that can be applied to gear B is
Explanation of Solution
Given information:
The allowable shearing stress
The diameter of the shaft AB
The diameter of the shaft CD
The radius of the gear B
The radius of the gear C
The length of the shaft AB
The length of the shaft CD
Assume that clockwise direction is negative and anticlockwise direction is positive.
Calculation:
Gear B and C:
Calculate the rotation in gear B
Substitute
Show the free body diagram of the gear C as in Figure 1.
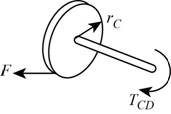
Calculate the force in the shaft CD (F) using the formula:
Show the free body diagram of the gear B as in Figure 2.

Calculate the torque produced in the shaft AB
Substitute
Substitute
Shaft AB:
Calculate the radius of the shaft AB
Substitute
Calculate the polar moment of inertia in the shaft AB
Substitute
Calculate the radius of the shaft CD
Substitute
Calculate the polar moment of inertia in the shaft CD
Substitute
Calculate the rotation about gear B
Substitute
Calculate the rotation about gear C
Substitute
Calculate the torque in CD
Substitute
Calculate the total torque (T) using the formula:
Consider the equation (2),
Substitute
Substitute
Calculate the torque in the shaft AB
Substitute
Substitute
Calculate the torque in the shaft CD
Substitute
Calculate the total torque (T):
Substitute
From the above calculated torque in the shaft AB and CD, take the lesser value.
Thus, the largest torque (T) that can be applied to gear B is
Want to see more full solutions like this?
Chapter 3 Solutions
Mechanics of Materials, 7th Edition
- 3,27 F'or the gear train shown, the diameters of the three solid shafts a dan = 20 mm dcp = 25 mm deF = 40 mm Knowing that for each shaft the allowable shearing stress is 60 MPa, determine the largest torque T that can be applied B 30 mm T 75 mm 30 mm 90 mm E Fig. P3.27arrow_forward3.48 The design of the gear-and-shaft system shown requires that steel shafts of the same diameter be used for both AB and CD. It is further required that 7ma60 MPa and that the angle d, through which end D of shaft CD rotates not exceed 1.5. Knowing that G = 77.2 GPa, determine the required diamcter of the shafts. 40 mm 1000 N m 100 mm 400 mm 600 mm Fig. P3.48arrow_forwardQ2/ The torques shown, in Fig. 2, are exerted on pulleys A and B. Knowing that the shafts are solid and made of steel (G=77 GPa), determine the maximum shear stress (t) of shaft BC, and then find the total angle of twist (0) between A and C. Fig. 2 TA Ta 300 N-m 30 mm 400 N-m 46 mm 0.9 m 0.75 m c!arrow_forward
- 3.27 A torque of magnitude T = 100 N •m is applied to shaft AB of the gear train shown. Knowing that the diameters of the three solid shafts are, respectively, das = 21 mm, dcp = 30 mm, and dgr = 40 mm, determine the maximum shearing stress in (a) shaft AB, (b) shaft CD, (c) shaft EF. 75 mm 30 mm 60 mm 25 mm Fig. P3.27 and P3.28arrow_forward3.41 plzarrow_forward3.36 The torques shown are exerted on pulleys B, C, and D. Knowing that the entire shaft is made of aluminum (G = 27 GPa), deter- mine the angle of twist between (a) C and B, (b) D and B. 30 mm 30 mm 400 N- m GG 36 mm 900 N- m 36 mm 500 N. m B "0.6 m E. 0.5 m D m 0.5 Fig. P3.36arrow_forward
- The solid spindle AB is made of a steel with an allowable shearing stress of 12 ksi, while sleeve CD is made of a brass with an allowable shearing stress of 7 ksi. Determine (a) the largest torque T that can be applied at A if the allowable shearing stress is not to be exceeded in sleeve CD, (b) the corresponding required value of the diameter ds of spindle ABarrow_forwardas shown, determine the angle of twist between (a) B and C, 3.35 The electric motor exerts a 500 N•m-torque on the aluminum shaft ABCD when it is rotating at a constant speed. Knowing that G = 27 GPa and that the torques exerted on pulleys B and C are as shown, determine the angle of twist between (a) R are 300 N. m 200 N - m 4S min 0.9 m B 44 mm 1.2 m 40 mm Fig. P3.35arrow_forward2.1arrow_forward
- 3.23 Under normal operating conditions a motor exerts a torque of magnitude T: at F. The shafts are made of a steel for which the allowable shearing stress is 82 MPa and have diameters dcDE = 24 mm and dran = 20 mm. Knowing that rp = 165 mm and rg = 114 mm, determine the largest allowable value of Tr. F. C T; B TEV E Fig. P3.23arrow_forwardTwo solid shafts are connected by gears as shown and are made of a steel for which the allowable shearing stress is 7000 psi. Knowing that the diameters of the two shafts are, respectively dBC= 1.6 in. and dEF= 1.25 in., determine the largest torque TC that can be applied at Carrow_forward3.46 The electric motor exerts a torque of 800 N · m on the steel shaft ABCD when it is rotating at a constant speed. Design specifications require that the diameter of the shaft be uniform from A to D and that the angle of twist between A and D not exceed 1.5°. Knowing that Tmas s 60 MPa and G = 77 GPa, determine the minimum diameter shaft that can be used. 300 N- m 500 N- m 04 m 0.6 m 0.3 m Fig. P3.46arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





