Chapter 2.2, Problem 26E

Solution

To Describe: The degree and leading coefficient of the graph of the polynomial function.

The degree of the polynomial function is odd, and the leading coefficient is negative.

Given graph:

  

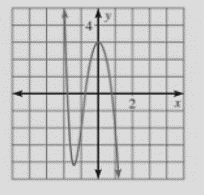
Concept Used:

In a graph if left end of the graph rises and right end falls: the degree of the equation will be odd, and the leading coefficient will be negative.

Description:

From the graph of the polynomial function, it is observed that $y$ rises to left as $x$ decreases and $y$ falls to the right as $x$ increases.

The end behaviour of the polynomial is $f\left(x\right)\to \infty$ as $x\to -\infty$ and $f\left(x\right)\to -\infty$ as $x\to \infty$ .

The degree should be odd the leading coefficient should be negative.

Conclusion:

Therefore, the degree of the polynomial function is odd, and the leading coefficient is negative.