6th Edition

ISBN: 9781133150572

Author: Redlin Watson Stewart

Publisher: Compliation @ Cengage Learning

See similar textbooks

Videos

Question

Chapter 1.9, Problem 74E

To determine

Graph the equation with the help of graphing calculator

Expert Solution & Answer

Answer to Problem 74E

Explanation of Solution

Given information:

Write a short essay describing different ways in which a graphing calculator might give a misleading graph of an equation.

Calculation:

A graphing calculator displays a rectangular portion of the graph of an equation in a display window or viewing screen, which we call a viewing rectangle. The default screen often gives an incomplete or misleading picture, so it is important to coose the viewing rectangle with care.

Let us graph the equation y=x2+3 with different viewing rectangles. We start with the viewing rectangle [−2,2]by[−2,2] . The resulting graph as shown below is blank.

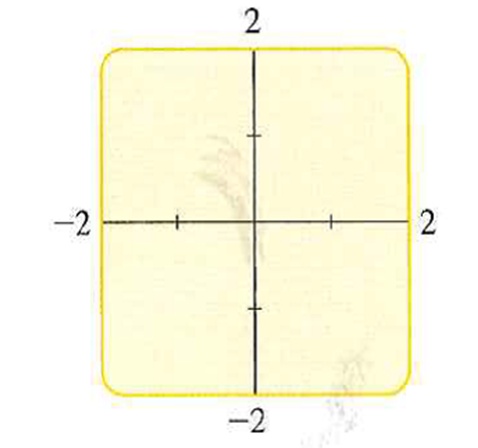
Precalculus - A Custom Text for UNLV, Chapter 1.9, Problem 74E , additional homework tip 1

This is because for all x ,

x2≥0x2+3≥3

Hence, the graph lies entirely above the viewing rectangle, so this viewing rectangle is not appropriate.

If we enlarge the viewing rectangle to [−4,4]by[−4,4] , as illustrated below, we begin to see a portion of the graph.

Precalculus - A Custom Text for UNLV, Chapter 1.9, Problem 74E , additional homework tip 2

If we enlarge the viewing rectangle to [−10,10]by[−5,30] , the graph seems to be more complete.

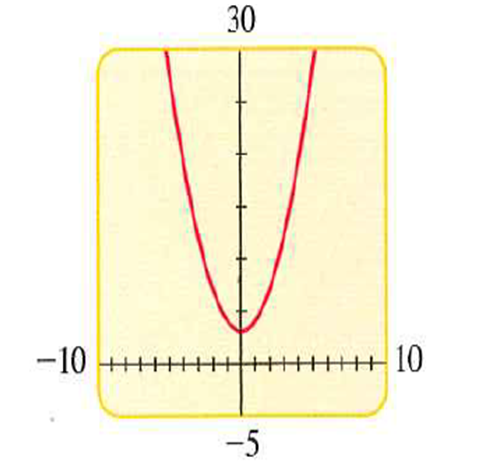
Precalculus - A Custom Text for UNLV, Chapter 1.9, Problem 74E , additional homework tip 3

Further enlarging the viewing rectangle, the graph do not show the y− intercept is 3 .

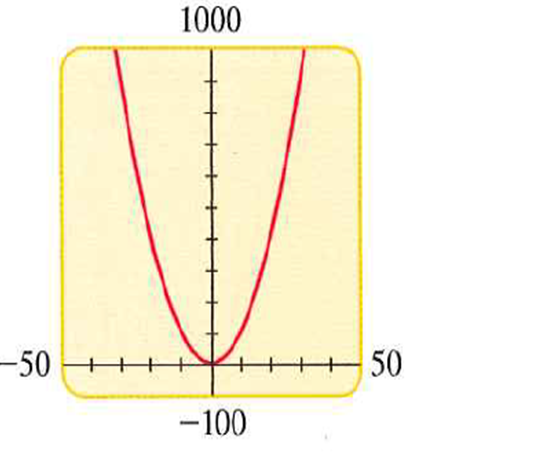
Precalculus - A Custom Text for UNLV, Chapter 1.9, Problem 74E , additional homework tip 4

Hence, the viewing rectangle to [−10,10]by[−5,30] is an appropriate representation of the graph.

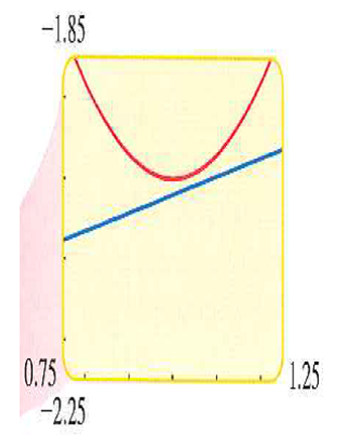
Now graph the equations y=3x2−6+1&y=0.23x−2.25 together in the viewing rectangle [−1,3]by[−2.5,1.5] . The graphs are so shown below.

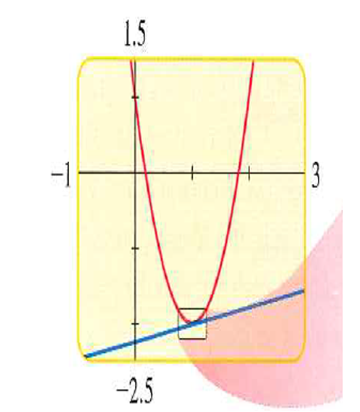
Precalculus - A Custom Text for UNLV, Chapter 1.9, Problem 74E , additional homework tip 5

One is a parabola, while the other is a line. It seems as if the graphs intersect near the point (1,−2) .

Hence, if we zoom in on the area around this point as illustrated below, we see that although the graphs almost touch, but they do not actually intersect.

Precalculus - A Custom Text for UNLV, Chapter 1.9, Problem 74E , additional homework tip 6

Chapter 1.9, Problem 73E

Chapter 1.9, Problem 75E

Chapter 1 Solutions

Precalculus - A Custom Text for UNLV

Ch. 1.1 - Give an example of each of the following: (a) A...Ch. 1.1 - Complete each statement and name the property of...Ch. 1.1 - Prob. 3E Ch. 1.1 - The symbol | x | stands for the __________of the...Ch. 1.1 - Prob. 5E Ch. 1.1 - Prob. 6E Ch. 1.1 - Prob. 7E Ch. 1.1 - Prob. 8E Ch. 1.1 - Prob. 9E Ch. 1.1 - Prob. 10E

Ch. 1.1 - Prob. 11E Ch. 1.1 - Prob. 12E Ch. 1.1 - Prob. 13E Ch. 1.1 - Prob. 14E Ch. 1.1 - Prob. 15E Ch. 1.1 - Prob. 16E Ch. 1.1 - Prob. 17E Ch. 1.1 - Prob. 18E Ch. 1.1 - Prob. 19E Ch. 1.1 - Prob. 20E Ch. 1.1 - Prob. 21E Ch. 1.1 - Prob. 22E Ch. 1.1 - Prob. 23E Ch. 1.1 - Prob. 24E Ch. 1.1 - Prob. 25E Ch. 1.1 - Prob. 26E Ch. 1.1 - Prob. 27E Ch. 1.1 - Prob. 28E Ch. 1.1 - Prob. 29E Ch. 1.1 - Prob. 30E Ch. 1.1 - Prob. 31E Ch. 1.1 - Prob. 32E Ch. 1.1 - Prob. 33E Ch. 1.1 - Prob. 34E Ch. 1.1 - Prob. 35E Ch. 1.1 - Prob. 36E Ch. 1.1 - Prob. 37E Ch. 1.1 - Prob. 38E Ch. 1.1 - Prob. 39E Ch. 1.1 - Prob. 40E Ch. 1.1 - Prob. 41E Ch. 1.1 - Prob. 42E Ch. 1.1 - Prob. 43E Ch. 1.1 - Prob. 44E Ch. 1.1 - Prob. 45E Ch. 1.1 - Prob. 46E Ch. 1.1 - Prob. 47E Ch. 1.1 - Prob. 48E Ch. 1.1 - Prob. 49E Ch. 1.1 - Prob. 50E Ch. 1.1 - Prob. 51E Ch. 1.1 - Prob. 52E Ch. 1.1 - Prob. 53E Ch. 1.1 - Prob. 54E Ch. 1.1 - Prob. 55E Ch. 1.1 - Prob. 56E Ch. 1.1 - Prob. 57E Ch. 1.1 - Prob. 58E Ch. 1.1 - Prob. 59E Ch. 1.1 - Prob. 60E Ch. 1.1 - Prob. 61E Ch. 1.1 - Prob. 62E Ch. 1.1 - Prob. 63E Ch. 1.1 - Prob. 64E Ch. 1.1 - Prob. 65E Ch. 1.1 - Prob. 66E Ch. 1.1 - Prob. 67E Ch. 1.1 - Prob. 68E Ch. 1.1 - Prob. 69E Ch. 1.1 - Prob. 70E Ch. 1.1 - Prob. 71E Ch. 1.1 - Prob. 72E Ch. 1.1 - Prob. 73E Ch. 1.1 - Prob. 74E Ch. 1.1 - Prob. 75E Ch. 1.1 - Prob. 76E Ch. 1.1 - Area of a Garden Marys backyard vegetable garden...Ch. 1.1 - Temperature Variation The bar graph shows the...Ch. 1.1 - Mailing a Package The post office will accept only...Ch. 1.1 - Prob. 80E Ch. 1.1 - Prob. 81E Ch. 1.1 - Prob. 82E Ch. 1.1 - Prob. 83E Ch. 1.1 - Prob. 84E Ch. 1.1 - Prob. 85E Ch. 1.2 - (a) Using exponential notation, we can write the...Ch. 1.2 - (a) When we multiply two powers with the same...Ch. 1.2 - Prob. 3E Ch. 1.2 - Explain what 43/2 means, then calculate 43/2 in...Ch. 1.2 - Explain how we rationalize a denominator, then...Ch. 1.2 - Find the missing power in the following...Ch. 1.2 - Prob. 7E Ch. 1.2 - Prob. 8E Ch. 1.2 - Prob. 9E Ch. 1.2 - Prob. 10E Ch. 1.2 - Prob. 11E Ch. 1.2 - Prob. 12E Ch. 1.2 - Prob. 13E Ch. 1.2 - Prob. 14E Ch. 1.2 - Prob. 15E Ch. 1.2 - Prob. 16E Ch. 1.2 - Prob. 17E Ch. 1.2 - Prob. 18E Ch. 1.2 - Prob. 19E Ch. 1.2 - Prob. 20E Ch. 1.2 - Prob. 21E Ch. 1.2 - Prob. 22E Ch. 1.2 - Prob. 23E Ch. 1.2 - Prob. 24E Ch. 1.2 - Prob. 25E Ch. 1.2 - Prob. 26E Ch. 1.2 - Prob. 27E Ch. 1.2 - Prob. 28E Ch. 1.2 - Prob. 29E Ch. 1.2 - Prob. 30E Ch. 1.2 - Prob. 31E Ch. 1.2 - Prob. 32E Ch. 1.2 - Prob. 33E Ch. 1.2 - Prob. 34E Ch. 1.2 - Prob. 35E Ch. 1.2 - Prob. 36E Ch. 1.2 - Prob. 37E Ch. 1.2 - Prob. 38E Ch. 1.2 - Prob. 39E Ch. 1.2 - Prob. 40E Ch. 1.2 - Prob. 41E Ch. 1.2 - Prob. 42E Ch. 1.2 - Prob. 43E Ch. 1.2 - Prob. 44E Ch. 1.2 - Prob. 45E Ch. 1.2 - Prob. 46E Ch. 1.2 - Prob. 47E Ch. 1.2 - Prob. 48E Ch. 1.2 - Prob. 49E Ch. 1.2 - Prob. 50E Ch. 1.2 - Prob. 51E Ch. 1.2 - Prob. 52E Ch. 1.2 - Prob. 53E Ch. 1.2 - Prob. 54E Ch. 1.2 - Prob. 55E Ch. 1.2 - Prob. 56E Ch. 1.2 - Prob. 57E Ch. 1.2 - Prob. 58E Ch. 1.2 - Prob. 59E Ch. 1.2 - Prob. 60E Ch. 1.2 - Prob. 61E Ch. 1.2 - Prob. 62E Ch. 1.2 - Prob. 63E Ch. 1.2 - Prob. 64E Ch. 1.2 - Prob. 65E Ch. 1.2 - Prob. 66E Ch. 1.2 - Prob. 67E Ch. 1.2 - Prob. 68E Ch. 1.2 - Prob. 69E Ch. 1.2 - Prob. 70E Ch. 1.2 - Prob. 71E Ch. 1.2 - Prob. 72E Ch. 1.2 - Prob. 73E Ch. 1.2 - Prob. 74E Ch. 1.2 - Prob. 75E Ch. 1.2 - Prob. 76E Ch. 1.2 - Prob. 77E Ch. 1.2 - Prob. 78E Ch. 1.2 - Prob. 79E Ch. 1.2 - Prob. 80E Ch. 1.2 - Prob. 81E Ch. 1.2 - Prob. 82E Ch. 1.2 - Prob. 83E Ch. 1.2 - Prob. 84E Ch. 1.2 - Prob. 85E Ch. 1.2 - Prob. 86E Ch. 1.2 - Prob. 87E Ch. 1.2 - Prob. 88E Ch. 1.2 - Prob. 89E Ch. 1.2 - Prob. 90E Ch. 1.2 - Prob. 91E Ch. 1.2 - Prob. 92E Ch. 1.2 - Prob. 93E Ch. 1.2 - Prob. 94E Ch. 1.2 - Prob. 95E Ch. 1.2 - Prob. 96E Ch. 1.2 - Volume of the Oceans The average ocean depth is...Ch. 1.2 - Prob. 98E Ch. 1.2 - Number of Molecules A sealed room in a hospital,...Ch. 1.2 - Prob. 100E Ch. 1.2 - Speed of a Skidding Car Police use the formula...Ch. 1.2 - Distance from the Earth to the Sun It follows from...Ch. 1.2 - Prob. 103E Ch. 1.2 - Prob. 104E Ch. 1.2 - Prob. 105E Ch. 1.2 - Prob. 106E Ch. 1.3 - Prob. 1E Ch. 1.3 - To factor the trinomial x2 + 7x + 10, we look for...Ch. 1.3 - The Special Product Formula for the square of a...Ch. 1.3 - The Special Product Formula for the product of the...Ch. 1.3 - Prob. 5E Ch. 1.3 - Prob. 6E Ch. 1.3 - Prob. 7E Ch. 1.3 - Prob. 8E Ch. 1.3 - Prob. 9E Ch. 1.3 - Prob. 10E Ch. 1.3 - Prob. 11E Ch. 1.3 - Prob. 12E Ch. 1.3 - Prob. 13E Ch. 1.3 - Prob. 14E Ch. 1.3 - Prob. 15E Ch. 1.3 - Prob. 16E Ch. 1.3 - Prob. 17E Ch. 1.3 - Prob. 18E Ch. 1.3 - Prob. 19E Ch. 1.3 - Prob. 20E Ch. 1.3 - Prob. 21E Ch. 1.3 - Prob. 22E Ch. 1.3 - Prob. 23E Ch. 1.3 - Prob. 24E Ch. 1.3 - Prob. 25E Ch. 1.3 - Prob. 26E Ch. 1.3 - Prob. 27E Ch. 1.3 - Prob. 28E Ch. 1.3 - Prob. 29E Ch. 1.3 - Prob. 30E Ch. 1.3 - Prob. 31E Ch. 1.3 - Prob. 32E Ch. 1.3 - Prob. 33E Ch. 1.3 - Prob. 34E Ch. 1.3 - Prob. 35E Ch. 1.3 - Prob. 36E Ch. 1.3 - Prob. 37E Ch. 1.3 - Prob. 38E Ch. 1.3 - Prob. 39E Ch. 1.3 - Prob. 40E Ch. 1.3 - Prob. 41E Ch. 1.3 - Prob. 42E Ch. 1.3 - Prob. 43E Ch. 1.3 - Prob. 44E Ch. 1.3 - Prob. 45E Ch. 1.3 - Prob. 46E Ch. 1.3 - Prob. 47E Ch. 1.3 - Prob. 48E Ch. 1.3 - Prob. 49E Ch. 1.3 - Prob. 50E Ch. 1.3 - Prob. 51E Ch. 1.3 - Prob. 52E Ch. 1.3 - Prob. 53E Ch. 1.3 - Prob. 54E Ch. 1.3 - Prob. 55E Ch. 1.3 - Prob. 56E Ch. 1.3 - Prob. 57E Ch. 1.3 - Prob. 58E Ch. 1.3 - Prob. 59E Ch. 1.3 - Prob. 60E Ch. 1.3 - Prob. 61E Ch. 1.3 - Prob. 62E Ch. 1.3 - Prob. 63E Ch. 1.3 - Prob. 64E Ch. 1.3 - Prob. 65E Ch. 1.3 - Prob. 66E Ch. 1.3 - Prob. 67E Ch. 1.3 - Prob. 68E Ch. 1.3 - Prob. 69E Ch. 1.3 - Prob. 70E Ch. 1.3 - Prob. 71E Ch. 1.3 - Prob. 72E Ch. 1.3 - Prob. 73E Ch. 1.3 - Prob. 74E Ch. 1.3 - Prob. 75E Ch. 1.3 - Prob. 76E Ch. 1.3 - Prob. 77E Ch. 1.3 - Prob. 78E Ch. 1.3 - Prob. 79E Ch. 1.3 - Prob. 80E Ch. 1.3 - Prob. 81E Ch. 1.3 - Prob. 82E Ch. 1.3 - Prob. 83E Ch. 1.3 - Prob. 84E Ch. 1.3 - Prob. 85E Ch. 1.3 - Prob. 86E Ch. 1.3 - Prob. 87E Ch. 1.3 - Prob. 88E Ch. 1.3 - Prob. 89E Ch. 1.3 - Prob. 90E Ch. 1.3 - Prob. 91E Ch. 1.3 - Prob. 92E Ch. 1.3 - Prob. 93E Ch. 1.3 - Prob. 94E Ch. 1.3 - Prob. 95E Ch. 1.3 - Prob. 96E Ch. 1.3 - Prob. 97E Ch. 1.3 - Prob. 98E Ch. 1.3 - Prob. 99E Ch. 1.3 - Prob. 100E Ch. 1.3 - Prob. 101E Ch. 1.3 - Prob. 102E Ch. 1.3 - Prob. 103E Ch. 1.3 - Prob. 104E Ch. 1.3 - Prob. 105E Ch. 1.3 - Prob. 106E Ch. 1.3 - Prob. 107E Ch. 1.3 - Prob. 108E Ch. 1.3 - Prob. 109E Ch. 1.3 - Prob. 110E Ch. 1.3 - Prob. 111E Ch. 1.3 - Prob. 112E Ch. 1.3 - Prob. 113E Ch. 1.3 - Prob. 114E Ch. 1.3 - Prob. 115E Ch. 1.3 - Prob. 116E Ch. 1.3 - Prob. 117E Ch. 1.3 - Prob. 118E Ch. 1.3 - Prob. 119E Ch. 1.3 - Prob. 120E Ch. 1.3 - Prob. 121E Ch. 1.3 - Prob. 122E Ch. 1.3 - Prob. 123E Ch. 1.3 - Prob. 124E Ch. 1.3 - Prob. 125E Ch. 1.3 - Prob. 126E Ch. 1.3 - Prob. 127E Ch. 1.3 - Prob. 128E Ch. 1.3 - Prob. 129E Ch. 1.3 - Prob. 130E Ch. 1.3 - Prob. 131E Ch. 1.3 - Prob. 132E Ch. 1.3 - Prob. 133E Ch. 1.3 - Prob. 134E Ch. 1.3 - Prob. 135E Ch. 1.3 - Prob. 136E Ch. 1.3 - Prob. 137E Ch. 1.4 - Which of the following are rational expressions?...Ch. 1.4 - To simplify a rational expression, we cancel...Ch. 1.4 - Prob. 3E Ch. 1.4 - Prob. 4E Ch. 1.4 - Prob. 5E Ch. 1.4 - Prob. 6E Ch. 1.4 - Prob. 7E Ch. 1.4 - Prob. 8E Ch. 1.4 - Prob. 9E Ch. 1.4 - Prob. 10E Ch. 1.4 - Prob. 11E Ch. 1.4 - Prob. 12E Ch. 1.4 - Prob. 13E Ch. 1.4 - Prob. 14E Ch. 1.4 - Prob. 15E Ch. 1.4 - Prob. 16E Ch. 1.4 - Prob. 17E Ch. 1.4 - Prob. 18E Ch. 1.4 - Prob. 19E Ch. 1.4 - Prob. 20E Ch. 1.4 - Prob. 21E Ch. 1.4 - Prob. 22E Ch. 1.4 - Prob. 23E Ch. 1.4 - Prob. 24E Ch. 1.4 - Prob. 25E Ch. 1.4 - Prob. 26E Ch. 1.4 - Prob. 27E Ch. 1.4 - Prob. 28E Ch. 1.4 - Prob. 29E Ch. 1.4 - Prob. 30E Ch. 1.4 - Prob. 31E Ch. 1.4 - Prob. 32E Ch. 1.4 - Prob. 33E Ch. 1.4 - Prob. 34E Ch. 1.4 - Prob. 35E Ch. 1.4 - Prob. 36E Ch. 1.4 - Prob. 37E Ch. 1.4 - Prob. 38E Ch. 1.4 - Prob. 39E Ch. 1.4 - Prob. 40E Ch. 1.4 - Prob. 41E Ch. 1.4 - Prob. 42E Ch. 1.4 - Prob. 43E Ch. 1.4 - Prob. 44E Ch. 1.4 - Prob. 45E Ch. 1.4 - Prob. 46E Ch. 1.4 - Prob. 47E Ch. 1.4 - Prob. 48E Ch. 1.4 - Prob. 49E Ch. 1.4 - Prob. 50E Ch. 1.4 - Prob. 51E Ch. 1.4 - Prob. 52E Ch. 1.4 - Prob. 53E Ch. 1.4 - Prob. 54E Ch. 1.4 - Prob. 55E Ch. 1.4 - Prob. 56E Ch. 1.4 - Prob. 57E Ch. 1.4 - Prob. 58E Ch. 1.4 - Prob. 59E Ch. 1.4 - Prob. 60E Ch. 1.4 - Prob. 61E Ch. 1.4 - Prob. 62E Ch. 1.4 - Prob. 63E Ch. 1.4 - Prob. 64E Ch. 1.4 - Prob. 65E Ch. 1.4 - Prob. 66E Ch. 1.4 - Prob. 67E Ch. 1.4 - Prob. 68E Ch. 1.4 - Prob. 69E Ch. 1.4 - Prob. 70E Ch. 1.4 - Prob. 71E Ch. 1.4 - Prob. 72E Ch. 1.4 - Prob. 73E Ch. 1.4 - Prob. 74E Ch. 1.4 - Prob. 75E Ch. 1.4 - Prob. 76E Ch. 1.4 - Prob. 77E Ch. 1.4 - Prob. 78E Ch. 1.4 - Prob. 79E Ch. 1.4 - Prob. 80E Ch. 1.4 - Prob. 81E Ch. 1.4 - Prob. 82E Ch. 1.4 - Prob. 83E Ch. 1.4 - Prob. 84E Ch. 1.4 - Prob. 85E Ch. 1.4 - Prob. 86E Ch. 1.4 - Prob. 87E Ch. 1.4 - Prob. 88E Ch. 1.4 - Prob. 89E Ch. 1.4 - Prob. 90E Ch. 1.4 - Prob. 91E Ch. 1.4 - Prob. 92E Ch. 1.4 - Prob. 93E Ch. 1.4 - Prob. 94E Ch. 1.4 - Prob. 95E Ch. 1.4 - Prob. 96E Ch. 1.4 - Prob. 97E Ch. 1.4 - Prob. 98E Ch. 1.4 - Prob. 99E Ch. 1.4 - Prob. 100E Ch. 1.4 - Prob. 101E Ch. 1.4 - Average Cost A clothing manufacturer finds that...Ch. 1.4 - Prob. 103E Ch. 1.4 - Prob. 104E Ch. 1.4 - Prob. 105E Ch. 1.4 - Prob. 106E Ch. 1.5 - Prob. 1E Ch. 1.5 - Explain how you would use each method to solve the...Ch. 1.5 - Prob. 3E Ch. 1.5 - Prob. 4E Ch. 1.5 - The equation (x + 1)2 5(x + 1) + 6 = 0 is...Ch. 1.5 - Prob. 6E Ch. 1.5 - Prob. 7E Ch. 1.5 - Prob. 8E Ch. 1.5 - Prob. 9E Ch. 1.5 - Prob. 10E Ch. 1.5 - Prob. 11E Ch. 1.5 - Prob. 12E Ch. 1.5 - Prob. 13E Ch. 1.5 - Prob. 14E Ch. 1.5 - Prob. 15E Ch. 1.5 - Prob. 16E Ch. 1.5 - Prob. 17E Ch. 1.5 - Prob. 18E Ch. 1.5 - Prob. 19E Ch. 1.5 - Prob. 20E Ch. 1.5 - Prob. 21E Ch. 1.5 - Prob. 22E Ch. 1.5 - Prob. 23E Ch. 1.5 - Prob. 24E Ch. 1.5 - Prob. 25E Ch. 1.5 - Prob. 26E Ch. 1.5 - Prob. 27E Ch. 1.5 - Prob. 28E Ch. 1.5 - Prob. 29E Ch. 1.5 - Prob. 30E Ch. 1.5 - Prob. 31E Ch. 1.5 - Prob. 32E Ch. 1.5 - Prob. 33E Ch. 1.5 - Prob. 34E Ch. 1.5 - Prob. 35E Ch. 1.5 - Prob. 36E Ch. 1.5 - Prob. 37E Ch. 1.5 - Prob. 38E Ch. 1.5 - Prob. 39E Ch. 1.5 - Prob. 40E Ch. 1.5 - Prob. 41E Ch. 1.5 - Prob. 42E Ch. 1.5 - Prob. 43E Ch. 1.5 - Prob. 44E Ch. 1.5 - Prob. 45E Ch. 1.5 - Prob. 46E Ch. 1.5 - Prob. 47E Ch. 1.5 - Prob. 48E Ch. 1.5 - Prob. 49E Ch. 1.5 - Prob. 50E Ch. 1.5 - Prob. 51E Ch. 1.5 - Prob. 52E Ch. 1.5 - Prob. 53E Ch. 1.5 - Prob. 54E Ch. 1.5 - Prob. 55E Ch. 1.5 - Prob. 56E Ch. 1.5 - Prob. 57E Ch. 1.5 - Prob. 58E Ch. 1.5 - Prob. 59E Ch. 1.5 - Prob. 60E Ch. 1.5 - Prob. 61E Ch. 1.5 - Prob. 62E Ch. 1.5 - Prob. 63E Ch. 1.5 - Prob. 64E Ch. 1.5 - Prob. 65E Ch. 1.5 - Prob. 66E Ch. 1.5 - Prob. 67E Ch. 1.5 - Prob. 68E Ch. 1.5 - Prob. 69E Ch. 1.5 - Prob. 70E Ch. 1.5 - Prob. 71E Ch. 1.5 - Prob. 72E Ch. 1.5 - Prob. 73E Ch. 1.5 - Prob. 74E Ch. 1.5 - Prob. 75E Ch. 1.5 - Prob. 76E Ch. 1.5 - Prob. 77E Ch. 1.5 - Prob. 78E Ch. 1.5 - Prob. 79E Ch. 1.5 - Prob. 80E Ch. 1.5 - Prob. 81E Ch. 1.5 - Prob. 82E Ch. 1.5 - Prob. 83E Ch. 1.5 - Prob. 84E Ch. 1.5 - Prob. 85E Ch. 1.5 - Prob. 86E Ch. 1.5 - Prob. 87E Ch. 1.5 - Prob. 88E Ch. 1.5 - Prob. 89E Ch. 1.5 - Prob. 90E Ch. 1.5 - Prob. 91E Ch. 1.5 - Prob. 92E Ch. 1.5 - Prob. 93E Ch. 1.5 - Prob. 94E Ch. 1.5 - Prob. 95E Ch. 1.5 - Prob. 96E Ch. 1.5 - Prob. 97E Ch. 1.5 - Prob. 98E Ch. 1.5 - Prob. 99E Ch. 1.5 - Prob. 100E Ch. 1.5 - Prob. 101E Ch. 1.5 - Prob. 102E Ch. 1.5 - Prob. 103E Ch. 1.5 - Prob. 104E Ch. 1.5 - Prob. 105E Ch. 1.5 - Prob. 106E Ch. 1.5 - Prob. 107E Ch. 1.5 - Prob. 108E Ch. 1.5 - Falling-Body Problems Suppose an object is dropped...Ch. 1.5 - Falling-Body Problems Suppose an object is dropped...Ch. 1.5 - Falling-Body Problems Use the formula h = 16t2 +...Ch. 1.5 - Prob. 112E Ch. 1.5 - Shrinkage in Concrete Beams As concrete dries, it...Ch. 1.5 - The Lens Equation If F is the focal length of a...Ch. 1.5 - Fish Population The fish population in a certain...Ch. 1.5 - Fish Population A large pond is stocked with fish....Ch. 1.5 - Profit A small-appliance manufacturer finds that...Ch. 1.5 - Gravity If an imaginary line segment is drawn...Ch. 1.5 - Depth of a Well One method for determining the...Ch. 1.5 - Prob. 120E Ch. 1.5 - Prob. 121E Ch. 1.5 - Prob. 122E Ch. 1.5 - Prob. 123E Ch. 1.5 - Prob. 124E Ch. 1.6 - Explain in your own words what it means for an...Ch. 1.6 - In the formula I = Prt for simple interest. P...Ch. 1.6 - Prob. 3E Ch. 1.6 - Balsamic vinegar contains 5% acetic acid, so a...Ch. 1.6 - Prob. 5E Ch. 1.6 - The formula d = rt models the distance d traveled...Ch. 1.6 - Prob. 7E Ch. 1.6 - Prob. 8E Ch. 1.6 - Prob. 9E Ch. 1.6 - Prob. 10E Ch. 1.6 - Prob. 11E Ch. 1.6 - Prob. 12E Ch. 1.6 - Prob. 13E Ch. 1.6 - Prob. 14E Ch. 1.6 - Prob. 15E Ch. 1.6 - Prob. 16E Ch. 1.6 - Prob. 17E Ch. 1.6 - Prob. 18E Ch. 1.6 - Prob. 19E Ch. 1.6 - Cell Phone Costs A cell phone company charges a...Ch. 1.6 - Investments Phyllis invested 12,000, a portion...Ch. 1.6 - Investments If Ben invests 4000 at 4% interest per...Ch. 1.6 - Prob. 23E Ch. 1.6 - Prob. 24E Ch. 1.6 - Salaries An executive in an engineering firm earns...Ch. 1.6 - Prob. 26E Ch. 1.6 - Prob. 27E Ch. 1.6 - Overtime Pay Helen earns 7.50 an hour at her job,...Ch. 1.6 - Prob. 29E Ch. 1.6 - Prob. 30E Ch. 1.6 - A Riddle A movie star, unwilling to give his age,...Ch. 1.6 - Career Home Runs During his major league career,...Ch. 1.6 - Value of Coins A change purse contains an equal...Ch. 1.6 - Value of Coins Mary has 3.00 in nickels, dimes,...Ch. 1.6 - Length of a Garden A rectangular garden is 25 ft...Ch. 1.6 - Prob. 36E Ch. 1.6 - Dimensions of a Lot A square plot of land has a...Ch. 1.6 - Prob. 38E Ch. 1.6 - Dimensions of a Garden A rectangular garden is 10...Ch. 1.6 - Prob. 40E Ch. 1.6 - Prob. 41E Ch. 1.6 - Prob. 42E Ch. 1.6 - Dimensions of a Lot A rectangular parcel of land...Ch. 1.6 - Dimensions of a Track A running track has the...Ch. 1.6 - Prob. 45E Ch. 1.6 - Prob. 46E Ch. 1.6 - Framing a Painting Ali paints with watercolors on...Ch. 1.6 - Dimensions of a Poster A poster has a rectangular...Ch. 1.6 - Prob. 49E Ch. 1.6 - Prob. 50E Ch. 1.6 - Length of a Shadow A man is walking away from a...Ch. 1.6 - Height of a Tree A woodcutter determines the...Ch. 1.6 - Prob. 53E Ch. 1.6 - Mixture Problem What amount of pure acid must be...Ch. 1.6 - Mixture Problem A jeweler has five rings, each...Ch. 1.6 - Mixture Problem A pot contains 6 L of brine at a...Ch. 1.6 - Mixture Problem The radiator in a car is filled...Ch. 1.6 - Prob. 58E Ch. 1.6 - Mixture Problem A bottle contains 750 mL of fruit...Ch. 1.6 - Mixture Problem A merchant blends tea that sells...Ch. 1.6 - Sharing a Job Candy and Tim share a paper route....Ch. 1.6 - Prob. 62E Ch. 1.6 - Sharing a Job Betty and Karen have been hired to...Ch. 1.6 - Sharing a Job Next-door neighbors Bob and Jim use...Ch. 1.6 - Sharing a Job Henry and Irene working together can...Ch. 1.6 - Sharing a Job Jack, Kay, and Lynn deliver...Ch. 1.6 - Distance, Speed, and Time Wendy took a trip from...Ch. 1.6 - Distance, Speed, and Time Two cyclists, 90 mi...Ch. 1.6 - Distance, Speed, and Time A pilot flew a jet from...Ch. 1.6 - Distance, Speed, and Time A woman driving a car 14...Ch. 1.6 - Distance, Speed, and Time A salesman drives from...Ch. 1.6 - Distance, Speed, and Time Kiran drove from Tortula...Ch. 1.6 - Distance, Speed, and Time It took a crew 2 h 40...Ch. 1.6 - Speed of a Boat Two fishing boats depart a harbor...Ch. 1.6 - Law of the Lever The figure shows a lever system,...Ch. 1.6 - Law of the Lever A plank 30 ft long rests on top...Ch. 1.6 - Dimensions of a Box A large plywood box has a...Ch. 1.6 - Prob. 78E Ch. 1.6 - Prob. 79E Ch. 1.6 - Prob. 80E Ch. 1.6 - Prob. 81E Ch. 1.6 - Dimensions of a Lot A city lot has the shape of a...Ch. 1.6 - Construction Costs The town of Foxton lies 10 mi...Ch. 1.6 - Distance, Speed, and Time A boardwalk is parallel...Ch. 1.6 - Volume of Grain Grain is falling from a chute onto...Ch. 1.6 - Prob. 86E Ch. 1.6 - Prob. 87E Ch. 1.6 - Prob. 88E Ch. 1.6 - An Ancient Chinese Problem This problem is taken...Ch. 1.6 - Prob. 90E Ch. 1.6 - Prob. 91E Ch. 1.7 - Fill in the blank with an appropriate inequality...Ch. 1.7 - Prob. 2E Ch. 1.7 - Prob. 3E Ch. 1.7 - (a) The set of all points on the real line whose...Ch. 1.7 - Prob. 5E Ch. 1.7 - Prob. 6E Ch. 1.7 - Prob. 7E Ch. 1.7 - Prob. 8E Ch. 1.7 - Prob. 9E Ch. 1.7 - Prob. 10E Ch. 1.7 - Prob. 11E Ch. 1.7 - Prob. 12E Ch. 1.7 - Prob. 13E Ch. 1.7 - Prob. 14E Ch. 1.7 - Prob. 15E Ch. 1.7 - Prob. 16E Ch. 1.7 - Prob. 17E Ch. 1.7 - Prob. 18E Ch. 1.7 - Prob. 19E Ch. 1.7 - Prob. 20E Ch. 1.7 - Prob. 21E Ch. 1.7 - Prob. 22E Ch. 1.7 - Prob. 23E Ch. 1.7 - Prob. 24E Ch. 1.7 - Prob. 25E Ch. 1.7 - Prob. 26E Ch. 1.7 - Prob. 27E Ch. 1.7 - Prob. 28E Ch. 1.7 - Prob. 29E Ch. 1.7 - Prob. 30E Ch. 1.7 - Prob. 31E Ch. 1.7 - Prob. 32E Ch. 1.7 - Prob. 33E Ch. 1.7 - Prob. 34E Ch. 1.7 - Prob. 35E Ch. 1.7 - Prob. 36E Ch. 1.7 - Prob. 37E Ch. 1.7 - Prob. 38E Ch. 1.7 - Prob. 39E Ch. 1.7 - Prob. 40E Ch. 1.7 - Prob. 41E Ch. 1.7 - Prob. 42E Ch. 1.7 - Prob. 43E Ch. 1.7 - Prob. 44E Ch. 1.7 - Prob. 45E Ch. 1.7 - Prob. 46E Ch. 1.7 - Prob. 47E Ch. 1.7 - Prob. 48E Ch. 1.7 - Prob. 49E Ch. 1.7 - Prob. 50E Ch. 1.7 - Prob. 51E Ch. 1.7 - Prob. 52E Ch. 1.7 - Prob. 53E Ch. 1.7 - Prob. 54E Ch. 1.7 - Prob. 55E Ch. 1.7 - Prob. 56E Ch. 1.7 - Prob. 57E Ch. 1.7 - Prob. 58E Ch. 1.7 - Prob. 59E Ch. 1.7 - Prob. 60E Ch. 1.7 - Prob. 61E Ch. 1.7 - Prob. 62E Ch. 1.7 - Prob. 63E Ch. 1.7 - Prob. 64E Ch. 1.7 - Prob. 65E Ch. 1.7 - Prob. 66E Ch. 1.7 - Prob. 67E Ch. 1.7 - Prob. 68E Ch. 1.7 - Prob. 69E Ch. 1.7 - Prob. 70E Ch. 1.7 - Prob. 71E Ch. 1.7 - Prob. 72E Ch. 1.7 - Prob. 73E Ch. 1.7 - Prob. 74E Ch. 1.7 - Prob. 75E Ch. 1.7 - Prob. 76E Ch. 1.7 - Prob. 77E Ch. 1.7 - Prob. 78E Ch. 1.7 - Prob. 79E Ch. 1.7 - Prob. 80E Ch. 1.7 - Prob. 81E Ch. 1.7 - Prob. 82E Ch. 1.7 - Prob. 83E Ch. 1.7 - Prob. 84E Ch. 1.7 - Prob. 85E Ch. 1.7 - Prob. 86E Ch. 1.7 - Prob. 87E Ch. 1.7 - Prob. 88E Ch. 1.7 - Prob. 89E Ch. 1.7 - Prob. 90E Ch. 1.7 - Prob. 91E Ch. 1.7 - Prob. 92E Ch. 1.7 - Prob. 93E Ch. 1.7 - Prob. 94E Ch. 1.7 - Prob. 95E Ch. 1.7 - Prob. 96E Ch. 1.7 - Prob. 97E Ch. 1.7 - Prob. 98E Ch. 1.7 - Prob. 99E Ch. 1.7 - Prob. 100E Ch. 1.7 - Prob. 101E Ch. 1.7 - Prob. 102E Ch. 1.7 - Prob. 103E Ch. 1.7 - Prob. 104E Ch. 1.7 - Prob. 105E Ch. 1.7 - Temperature Scales What interval on the Celsius...Ch. 1.7 - Prob. 107E Ch. 1.7 - International Plans A phone service provider...Ch. 1.7 - Driving Cost It is estimated that the annual cost...Ch. 1.7 - Air Temperature As dry air moves upward, it...Ch. 1.7 - Airline Ticket Price A charter airline finds that...Ch. 1.7 - Accuracy of a Scale A coffee merchant sells a...Ch. 1.7 - Prob. 113E Ch. 1.7 - Bonfire Temperature In the vicinity of a bonfire...Ch. 1.7 - Falling Ball Using calculus, it can be shown that...Ch. 1.7 - Gas Mileage The gas mileage g (measured in mi/gal)...Ch. 1.7 - Stopping Distance For a certain model of car the...Ch. 1.7 - Prob. 118E Ch. 1.7 - Fencing a Garden A determined gardener has 120 ft...Ch. 1.7 - Thickness of a Laminate A company manufactures...Ch. 1.7 - Range of Height The average height of adult males...Ch. 1.7 - Prob. 122E Ch. 1.7 - Prob. 123E Ch. 1.7 - Prob. 124E Ch. 1.8 - The point that is 3 units to the right of the...Ch. 1.8 - Prob. 2E Ch. 1.8 - The point midway between (a, b) and (c, d) is...Ch. 1.8 - Prob. 4E Ch. 1.8 - Prob. 5E Ch. 1.8 - Prob. 6E Ch. 1.8 - Prob. 7E Ch. 1.8 - Prob. 8E Ch. 1.8 - Prob. 9E Ch. 1.8 - Prob. 10E Ch. 1.8 - Prob. 11E Ch. 1.8 - Prob. 12E Ch. 1.8 - Prob. 13E Ch. 1.8 - Prob. 14E Ch. 1.8 - Prob. 15E Ch. 1.8 - Prob. 16E Ch. 1.8 - Prob. 17E Ch. 1.8 - Prob. 18E Ch. 1.8 - Prob. 19E Ch. 1.8 - Prob. 20E Ch. 1.8 - Prob. 21E Ch. 1.8 - Prob. 22E Ch. 1.8 - Prob. 23E Ch. 1.8 - Prob. 24E Ch. 1.8 - Prob. 25E Ch. 1.8 - Prob. 26E Ch. 1.8 - Prob. 27E Ch. 1.8 - Prob. 28E Ch. 1.8 - Prob. 29E Ch. 1.8 - Prob. 30E Ch. 1.8 - Prob. 31E Ch. 1.8 - Prob. 32E Ch. 1.8 - Prob. 33E Ch. 1.8 - Prob. 34E Ch. 1.8 - Prob. 35E Ch. 1.8 - Prob. 36E Ch. 1.8 - Prob. 37E Ch. 1.8 - Prob. 38E Ch. 1.8 - Prob. 39E Ch. 1.8 - Prob. 40E Ch. 1.8 - Prob. 41E Ch. 1.8 - Prob. 42E Ch. 1.8 - Prob. 43E Ch. 1.8 - Prob. 44E Ch. 1.8 - Prob. 45E Ch. 1.8 - Prob. 46E Ch. 1.8 - Prob. 47E Ch. 1.8 - Prob. 48E Ch. 1.8 - Prob. 49E Ch. 1.8 - Prob. 50E Ch. 1.8 - Prob. 51E Ch. 1.8 - Prob. 52E Ch. 1.8 - Prob. 53E Ch. 1.8 - Prob. 54E Ch. 1.8 - Prob. 55E Ch. 1.8 - Prob. 56E Ch. 1.8 - Prob. 57E Ch. 1.8 - Prob. 58E Ch. 1.8 - Prob. 59E Ch. 1.8 - Prob. 60E Ch. 1.8 - Prob. 61E Ch. 1.8 - Prob. 62E Ch. 1.8 - Prob. 63E Ch. 1.8 - Prob. 64E Ch. 1.8 - Prob. 65E Ch. 1.8 - Prob. 66E Ch. 1.8 - Prob. 67E Ch. 1.8 - Prob. 68E Ch. 1.8 - Prob. 69E Ch. 1.8 - Prob. 70E Ch. 1.8 - Prob. 71E Ch. 1.8 - Prob. 72E Ch. 1.8 - Prob. 73E Ch. 1.8 - Prob. 74E Ch. 1.8 - Prob. 75E Ch. 1.8 - Prob. 76E Ch. 1.8 - Prob. 77E Ch. 1.8 - Prob. 78E Ch. 1.8 - Prob. 79E Ch. 1.8 - Prob. 80E Ch. 1.8 - Prob. 81E Ch. 1.8 - Prob. 82E Ch. 1.8 - Prob. 83E Ch. 1.8 - Prob. 84E Ch. 1.8 - Prob. 85E Ch. 1.8 - Prob. 86E Ch. 1.8 - Prob. 87E Ch. 1.8 - Prob. 88E Ch. 1.8 - Prob. 89E Ch. 1.8 - Prob. 90E Ch. 1.8 - Prob. 91E Ch. 1.8 - Prob. 92E Ch. 1.8 - Prob. 93E Ch. 1.8 - Prob. 94E Ch. 1.8 - Prob. 95E Ch. 1.8 - Prob. 96E Ch. 1.8 - Prob. 97E Ch. 1.8 - Prob. 98E Ch. 1.8 - Prob. 99E Ch. 1.8 - Prob. 100E Ch. 1.8 - Prob. 101E Ch. 1.8 - Prob. 102E Ch. 1.8 - Prob. 103E Ch. 1.8 - Prob. 104E Ch. 1.8 - Prob. 105E Ch. 1.8 - Prob. 106E Ch. 1.8 - Prob. 107E Ch. 1.8 - Prob. 108E Ch. 1.8 - Prob. 109E Ch. 1.8 - Prob. 110E Ch. 1.8 - Prob. 111E Ch. 1.8 - Prob. 112E Ch. 1.8 - Distances in a City A city has streets that run...Ch. 1.8 - Halfway Point Two friends live in the city...Ch. 1.8 - Orbit of a Satellite A satellite is in orbit...Ch. 1.8 - Prob. 116E Ch. 1.8 - Prob. 117E Ch. 1.8 - Prob. 118E Ch. 1.8 - Prob. 119E Ch. 1.8 - Prob. 120E Ch. 1.8 - Prob. 121E Ch. 1.8 - Prob. 122E Ch. 1.9 - Prob. 1E Ch. 1.9 - Prob. 2E Ch. 1.9 - Prob. 3E Ch. 1.9 - Prob. 4E Ch. 1.9 - Prob. 5E Ch. 1.9 - Prob. 6E Ch. 1.9 - Prob. 7E Ch. 1.9 - Prob. 8E Ch. 1.9 - Prob. 9E Ch. 1.9 - Prob. 10E Ch. 1.9 - Prob. 11E Ch. 1.9 - Prob. 12E Ch. 1.9 - Prob. 13E Ch. 1.9 - Prob. 14E Ch. 1.9 - Prob. 15E Ch. 1.9 - Prob. 16E Ch. 1.9 - Prob. 17E Ch. 1.9 - Prob. 18E Ch. 1.9 - Prob. 19E Ch. 1.9 - Prob. 20E Ch. 1.9 - Prob. 21E Ch. 1.9 - Prob. 22E Ch. 1.9 - Prob. 23E Ch. 1.9 - Prob. 24E Ch. 1.9 - Prob. 25E Ch. 1.9 - Prob. 26E Ch. 1.9 - Prob. 27E Ch. 1.9 - Prob. 28E Ch. 1.9 - Prob. 29E Ch. 1.9 - Prob. 30E Ch. 1.9 - Prob. 31E Ch. 1.9 - Prob. 32E Ch. 1.9 - Prob. 33E Ch. 1.9 - Prob. 34E Ch. 1.9 - Prob. 35E Ch. 1.9 - Prob. 36E Ch. 1.9 - Prob. 37E Ch. 1.9 - Prob. 38E Ch. 1.9 - Prob. 39E Ch. 1.9 - Prob. 40E Ch. 1.9 - Prob. 41E Ch. 1.9 - Prob. 42E Ch. 1.9 - Prob. 43E Ch. 1.9 - Prob. 44E Ch. 1.9 - Prob. 45E Ch. 1.9 - Prob. 46E Ch. 1.9 - Prob. 47E Ch. 1.9 - Prob. 48E Ch. 1.9 - Prob. 49E Ch. 1.9 - Prob. 50E Ch. 1.9 - Prob. 51E Ch. 1.9 - Prob. 52E Ch. 1.9 - Prob. 53E Ch. 1.9 - Prob. 54E Ch. 1.9 - Prob. 55E Ch. 1.9 - Prob. 56E Ch. 1.9 - Prob. 57E Ch. 1.9 - Prob. 58E Ch. 1.9 - Prob. 59E Ch. 1.9 - Prob. 60E Ch. 1.9 - Prob. 61E Ch. 1.9 - Prob. 62E Ch. 1.9 - Prob. 63E Ch. 1.9 - Prob. 64E Ch. 1.9 - Prob. 65E Ch. 1.9 - Prob. 66E Ch. 1.9 - Prob. 67E Ch. 1.9 - Prob. 68E Ch. 1.9 - Prob. 69E Ch. 1.9 - Prob. 70E Ch. 1.9 - Prob. 71E Ch. 1.9 - Prob. 72E Ch. 1.9 - Prob. 73E Ch. 1.9 - Prob. 74E Ch. 1.9 - Prob. 75E Ch. 1.9 - Prob. 76E Ch. 1.9 - Prob. 77E Ch. 1.10 - We find the steepness, or slope, of a line passing...Ch. 1.10 - Prob. 2E Ch. 1.10 - Prob. 3E Ch. 1.10 - Prob. 4E Ch. 1.10 - Prob. 5E Ch. 1.10 - Prob. 6E Ch. 1.10 - Prob. 7E Ch. 1.10 - Prob. 8E Ch. 1.10 - Prob. 9E Ch. 1.10 - Prob. 10E Ch. 1.10 - Prob. 11E Ch. 1.10 - Prob. 12E Ch. 1.10 - Prob. 13E Ch. 1.10 - Prob. 14E Ch. 1.10 - Prob. 15E Ch. 1.10 - Prob. 16E Ch. 1.10 - Prob. 17E Ch. 1.10 - Prob. 18E Ch. 1.10 - Prob. 19E Ch. 1.10 - Prob. 20E Ch. 1.10 - Prob. 21E Ch. 1.10 - Prob. 22E Ch. 1.10 - Prob. 23E Ch. 1.10 - Prob. 24E Ch. 1.10 - Prob. 25E Ch. 1.10 - Prob. 26E Ch. 1.10 - Prob. 27E Ch. 1.10 - Prob. 28E Ch. 1.10 - Prob. 29E Ch. 1.10 - Prob. 30E Ch. 1.10 - Prob. 31E Ch. 1.10 - Prob. 32E Ch. 1.10 - Prob. 33E Ch. 1.10 - Prob. 34E Ch. 1.10 - Prob. 35E Ch. 1.10 - Prob. 36E Ch. 1.10 - Prob. 37E Ch. 1.10 - Prob. 38E Ch. 1.10 - Prob. 39E Ch. 1.10 - Prob. 40E Ch. 1.10 - Prob. 41E Ch. 1.10 - Prob. 42E Ch. 1.10 - Prob. 43E Ch. 1.10 - Prob. 44E Ch. 1.10 - Prob. 45E Ch. 1.10 - Prob. 46E Ch. 1.10 - Prob. 47E Ch. 1.10 - Prob. 48E Ch. 1.10 - Prob. 49E Ch. 1.10 - Prob. 50E Ch. 1.10 - Prob. 51E Ch. 1.10 - Prob. 52E Ch. 1.10 - Prob. 53E Ch. 1.10 - Prob. 54E Ch. 1.10 - Prob. 55E Ch. 1.10 - Prob. 56E Ch. 1.10 - Prob. 57E Ch. 1.10 - Prob. 58E Ch. 1.10 - Prob. 59E Ch. 1.10 - Prob. 60E Ch. 1.10 - Prob. 61E Ch. 1.10 - Prob. 62E Ch. 1.10 - Prob. 63E Ch. 1.10 - Prob. 64E Ch. 1.10 - Prob. 65E Ch. 1.10 - Prob. 66E Ch. 1.10 - Drug Dosages If the recommended adult dosage for a...Ch. 1.10 - Flea Market The manager of a weekend flea market...Ch. 1.10 - Prob. 69E Ch. 1.10 - Prob. 70E Ch. 1.10 - Prob. 71E Ch. 1.10 - Depreciation A small business buys a computer for...Ch. 1.10 - Prob. 73E Ch. 1.10 - Prob. 74E Ch. 1.10 - Prob. 75E Ch. 1.10 - Prob. 76E Ch. 1.10 - Prob. 77E Ch. 1.10 - Prob. 78E Ch. 1.11 - If the quantities x and y are related by the...Ch. 1.11 - Prob. 2E Ch. 1.11 - Prob. 3E Ch. 1.11 - Prob. 4E Ch. 1.11 - Prob. 5E Ch. 1.11 - Prob. 6E Ch. 1.11 - Prob. 7E Ch. 1.11 - Prob. 8E Ch. 1.11 - Prob. 9E Ch. 1.11 - Prob. 10E Ch. 1.11 - Prob. 11E Ch. 1.11 - Prob. 12E Ch. 1.11 - Prob. 13E Ch. 1.11 - Prob. 14E Ch. 1.11 - Prob. 15E Ch. 1.11 - Prob. 16E Ch. 1.11 - Prob. 17E Ch. 1.11 - Prob. 18E Ch. 1.11 - Prob. 19E Ch. 1.11 - Prob. 20E Ch. 1.11 - Prob. 21E Ch. 1.11 - Prob. 22E Ch. 1.11 - Prob. 23E Ch. 1.11 - Prob. 24E Ch. 1.11 - Prob. 25E Ch. 1.11 - Prob. 26E Ch. 1.11 - Prob. 27E Ch. 1.11 - Prob. 28E Ch. 1.11 - Hookes Law Hookes Law states that the force needed...Ch. 1.11 - Prob. 30E Ch. 1.11 - Prob. 31E Ch. 1.11 - Prob. 32E Ch. 1.11 - Prob. 33E Ch. 1.11 - Prob. 34E Ch. 1.11 - Prob. 35E Ch. 1.11 - Stopping Distance The stopping distance D of a car...Ch. 1.11 - Prob. 37E Ch. 1.11 - Aerodynamic Lift The lift L on an airplane wing at...Ch. 1.11 - Drag Force on a Boat The drag force F on a boat is...Ch. 1.11 - Prob. 40E Ch. 1.11 - Prob. 41E Ch. 1.11 - Keplers Third Law Keplers Third Law of planetary...Ch. 1.11 - Radiation Energy The total radiation energy E...Ch. 1.11 - Value of a Lot The value of a building lot on...Ch. 1.11 - Prob. 45E Ch. 1.11 - Prob. 46E Ch. 1.11 - Frequency of Vibration The frequency f of...Ch. 1.11 - Spread of a Disease The rate r at which a disease...Ch. 1.11 - Prob. 49E Ch. 1 - Prob. 1RCC Ch. 1 - Prob. 2RCC Ch. 1 - Prob. 3RCC Ch. 1 - Prob. 4RCC Ch. 1 - Prob. 5RCC Ch. 1 - Prob. 6RCC Ch. 1 - Prob. 7RCC Ch. 1 - Prob. 8RCC Ch. 1 - Prob. 9RCC Ch. 1 - Prob. 10RCC Ch. 1 - Prob. 11RCC Ch. 1 - Prob. 12RCC Ch. 1 - Prob. 13RCC Ch. 1 - Prob. 14RCC Ch. 1 - Prob. 15RCC Ch. 1 - Prob. 16RCC Ch. 1 - Prob. 17RCC Ch. 1 - Prob. 18RCC Ch. 1 - Prob. 19RCC Ch. 1 - Prob. 20RCC Ch. 1 - Prob. 21RCC Ch. 1 - Prob. 22RCC Ch. 1 - Prob. 23RCC Ch. 1 - Prob. 24RCC Ch. 1 - How do you find x-intercepts and y-intercepts of a...Ch. 1 - Prob. 26RCC Ch. 1 - Prob. 27RCC Ch. 1 - Prob. 28RCC Ch. 1 - Prob. 29RCC Ch. 1 - Prob. 30RCC Ch. 1 - Prob. 31RCC Ch. 1 - Prob. 32RCC Ch. 1 - Prob. 33RCC Ch. 1 - Prob. 1RE Ch. 1 - Prob. 2RE Ch. 1 - Prob. 3RE Ch. 1 - Prob. 4RE Ch. 1 - Prob. 5RE Ch. 1 - Prob. 6RE Ch. 1 - Prob. 7RE Ch. 1 - Prob. 8RE Ch. 1 - Prob. 9RE Ch. 1 - Prob. 10RE Ch. 1 - Prob. 11RE Ch. 1 - Prob. 12RE Ch. 1 - Prob. 13RE Ch. 1 - Prob. 14RE Ch. 1 - Prob. 15RE Ch. 1 - Prob. 16RE Ch. 1 - Prob. 17RE Ch. 1 - Prob. 18RE Ch. 1 - Prob. 19RE Ch. 1 - Prob. 20RE Ch. 1 - Prob. 21RE Ch. 1 - Prob. 22RE Ch. 1 - Prob. 23RE Ch. 1 - Prob. 24RE Ch. 1 - Prob. 25RE Ch. 1 - Prob. 26RE Ch. 1 - Prob. 27RE Ch. 1 - Prob. 28RE Ch. 1 - Prob. 29RE Ch. 1 - Prob. 30RE Ch. 1 - Prob. 31RE Ch. 1 - Prob. 32RE Ch. 1 - Prob. 33RE Ch. 1 - Prob. 34RE Ch. 1 - Prob. 35RE Ch. 1 - Prob. 36RE Ch. 1 - Prob. 37RE Ch. 1 - Prob. 38RE Ch. 1 - Prob. 39RE Ch. 1 - Prob. 40RE Ch. 1 - Prob. 41RE Ch. 1 - Prob. 42RE Ch. 1 - Prob. 43RE Ch. 1 - Prob. 44RE Ch. 1 - Prob. 45RE Ch. 1 - Prob. 46RE Ch. 1 - Prob. 47RE Ch. 1 - Prob. 48RE Ch. 1 - Prob. 49RE Ch. 1 - Prob. 50RE Ch. 1 - Prob. 51RE Ch. 1 - Prob. 52RE Ch. 1 - Prob. 53RE Ch. 1 - Prob. 54RE Ch. 1 - Prob. 55RE Ch. 1 - Prob. 56RE Ch. 1 - Prob. 57RE Ch. 1 - Prob. 58RE Ch. 1 - Prob. 59RE Ch. 1 - Prob. 60RE Ch. 1 - Prob. 61RE Ch. 1 - Prob. 62RE Ch. 1 - Prob. 63RE Ch. 1 - Prob. 64RE Ch. 1 - Prob. 65RE Ch. 1 - Prob. 66RE Ch. 1 - Prob. 67RE Ch. 1 - Prob. 68RE Ch. 1 - Prob. 69RE Ch. 1 - Prob. 70RE Ch. 1 - Prob. 71RE Ch. 1 - Prob. 72RE Ch. 1 - Prob. 73RE Ch. 1 - Prob. 74RE Ch. 1 - Prob. 75RE Ch. 1 - Prob. 76RE Ch. 1 - Prob. 77RE Ch. 1 - Prob. 78RE Ch. 1 - Prob. 79RE Ch. 1 - Prob. 80RE Ch. 1 - Prob. 81RE Ch. 1 - Prob. 82RE Ch. 1 - Prob. 83RE Ch. 1 - Prob. 84RE Ch. 1 - Prob. 85RE Ch. 1 - Prob. 86RE Ch. 1 - Prob. 87RE Ch. 1 - Prob. 88RE Ch. 1 - Prob. 89RE Ch. 1 - Prob. 90RE Ch. 1 - Prob. 91RE Ch. 1 - Prob. 92RE Ch. 1 - Prob. 93RE Ch. 1 - Prob. 94RE Ch. 1 - Prob. 95RE Ch. 1 - Prob. 96RE Ch. 1 - Prob. 97RE Ch. 1 - Prob. 98RE Ch. 1 - Prob. 99RE Ch. 1 - Prob. 100RE Ch. 1 - Prob. 101RE Ch. 1 - Prob. 102RE Ch. 1 - Prob. 103RE Ch. 1 - Prob. 104RE Ch. 1 - Prob. 105RE Ch. 1 - Prob. 106RE Ch. 1 - Prob. 107RE Ch. 1 - Prob. 108RE Ch. 1 - Prob. 109RE Ch. 1 - Prob. 110RE Ch. 1 - Prob. 111RE Ch. 1 - Prob. 112RE Ch. 1 - Prob. 113RE Ch. 1 - Prob. 114RE Ch. 1 - Prob. 115RE Ch. 1 - Prob. 116RE Ch. 1 - Prob. 117RE Ch. 1 - Prob. 118RE Ch. 1 - Prob. 119RE Ch. 1 - Prob. 120RE Ch. 1 - Prob. 121RE Ch. 1 - Prob. 122RE Ch. 1 - Prob. 123RE Ch. 1 - Prob. 124RE Ch. 1 - Prob. 125RE Ch. 1 - Prob. 126RE Ch. 1 - Prob. 127RE Ch. 1 - Prob. 128RE Ch. 1 - Prob. 129RE Ch. 1 - Prob. 130RE Ch. 1 - Prob. 131RE Ch. 1 - Prob. 132RE Ch. 1 - Prob. 133RE Ch. 1 - Prob. 134RE Ch. 1 - Prob. 135RE Ch. 1 - Prob. 136RE Ch. 1 - Prob. 137RE Ch. 1 - Prob. 138RE Ch. 1 - (a) Graph the intervals (5, 3] and (2, ) on the...Ch. 1 - Prob. 2T Ch. 1 - Write each number in scientific notation. (a)...Ch. 1 - Simplify each expression. Write your final answer...Ch. 1 - Prob. 5T Ch. 1 - Prob. 6T Ch. 1 - Prob. 7T Ch. 1 - Prob. 8T Ch. 1 - Mary drove from Amity to Belleville at a speed of...Ch. 1 - Prob. 10T Ch. 1 - Prob. 11T Ch. 1 - A bottle of medicine is to be stored at a...Ch. 1 - Prob. 13T Ch. 1 - Prob. 14T Ch. 1 - (a) Plot the points P(0, 3), Q(3, 0), and R(6, 3)...Ch. 1 - Prob. 16T Ch. 1 - Prob. 17T Ch. 1 - Prob. 18T Ch. 1 - Write the linear equation 2x 3y = 15 in...Ch. 1 - Prob. 20T Ch. 1 - A geologist measures the temperature T (in C) of...Ch. 1 - The maximum weight M that can be supported by a...Ch. 1 - Femur Length and Height Anthropologists use a...Ch. 1 - Demand for Soft Drinks A convenience store manager...Ch. 1 - Prob. 3P Ch. 1 - Prob. 4P Ch. 1 - Prob. 5P Ch. 1 - Prob. 6P Ch. 1 - Prob. 7P Ch. 1 - Noise and Intelligibility Audiologists study the...Ch. 1 - Life Expectancy The average life expectancy in the...Ch. 1 - Prob. 10P Ch. 1 - Prob. 11P Ch. 1 - Prob. 12P Ch. 1 - Prob. 13P

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.