
Concept explainers
Hooke’s Law Hooke’s Law states that the force needed to keep a spring stretched x units beyond its natural length is directly proportional to x. Here the constant of proportionality is called the spring constant.
- (a) Write Hooke’s Law as an equation.
- (b) If a spring has a natural length of 5 cm and a force of 30 N is required to maintain the spring stretched to a length of 9 cm, find the spring constant.
- (c) What force is needed to keep the spring stretched to a length of 11 cm?
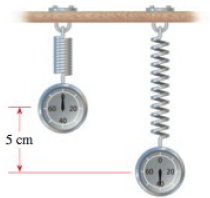
(a)
To express: Hooke’s law for spring as equation.
Answer to Problem 29E
Hooke’s law for spring is
Explanation of Solution
Hooke’s law:
The force required to keep the spring stretched beyond the natural length is directly proportional to the extension of spring beyond natural length.
Mathematically,
Here,
Thus, Hooke’s law as an equation is
(b)
To find: The spring constant
Answer to Problem 29E
The value of spring constant is
Explanation of Solution
Given:
Natural length of spring (
Force required to stretch it up to
Calculation:
The spring is stretched up to
Use Hooke’s Law,
Substitute, 30 for
Multiply both the sides by
Thus, the value of
(c)
To find: The force required to keep the spring stretched to
Answer to Problem 29E
The force required is
Explanation of Solution
Given:
The stretched length of the spring is
Calculation:
The natural length of spring is
Use Hooke’s Law,
Substitute 6 for
Thus, the value of
Chapter 1 Solutions
Precalculus - A Custom Text for UNLV
- A region is bounded by y = 0, y = x³, and x = 1. Find the x coordinate of the center of mass. Round off to two decimal places. Remember if A is the area of the region then 1 x = ffxdydx Aarrow_forwardy=ln((1+e^x)/(1-e^x)) find the derivative.arrow_forwardfind the curvature when t = 0.5. round off to two decimal places. r(t) = <t, 1/2t^2, 1/2t^2>arrow_forward
- find the speed of the object when t=2. Give the answer in decimal form and round to 2 decimal places. r(t) = <3t-1,t^2>arrow_forward3. Evaluate. Leave your answer in simplest exact form: 8 x²+x+1 √x dxarrow_forwardFind the eccentricity. x2/25 + y2/9 = 1. Round off to two decimal places.arrow_forward
- x(t) =2t2-t y(t) = 1-3 Find dy/dx when t = 0. Round off to two decimal places.arrow_forward2. Find the function f(x) given that f'(x) = 3cos (x) - 2sin(x) and f(π/6)=√3. Leave your answer in exact simplest form and check your answer.arrow_forward1. Evaluate the limit. Show all steps and simplify answers. lim 7x - 4ex x+2x+5exarrow_forward
- Evaluate the definite integral. Sketch the area of the region given by the definite integral. Leave your answer in exact simplest form. Check your answer using your calculator. S² (x² - 4x + 4) dxarrow_forwardhow do i estimate the area under the graph of f(x) = 2 cos(x) from x=0 to x= T / 2 using four approximate rectangles and right endpoints . how would i round it to 4 decimal places? And how would the graph with the shaded rectangles look like ? would it be an overestimate? the last person gave me an AI answer but i need a written paper to understand. please show me what the graph exactly looks like. thank you so mucharrow_forwardIm confused on part darrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





