6th Edition

ISBN: 9781133150572

Author: Redlin Watson Stewart

Publisher: Compliation @ Cengage Learning

Concept explainers

A family of curves is a group of curves that are each described by a parametrization in which one or more variables are parameters. In general, the parameters have more complexity on the assembly of the curve than an ordinary linear transformation. These…

XZ Plane

In order to understand XZ plane, it's helpful to understand two-dimensional and three-dimensional spaces. To plot a point on a plane, two numbers are needed, and these two numbers in the plane can be represented as an ordered pair (a,b) where a and b are…

Euclidean Geometry

Geometry is the branch of mathematics that deals with flat surfaces like lines, angles, points, two-dimensional figures, etc. In Euclidean geometry, one studies the geometrical shapes that rely on different theorems and axioms. This (pure mathematics) ge…

Lines and Angles

In a two-dimensional plane, a line is simply a figure that joins two points. Usually, lines are used for presenting objects that are straight in shape and have minimal depth or width.

Videos

Textbook Question

Chapter 1.10, Problem 68E

Flea Market The manager of a weekend flea market knows from past experience that if she charges x dollars for a rental space at the flea market, then the number y of spaces she can rent is given by the equation y = 200 − 4x.

(a) Sketch a graph of this linear equation. (Remember that the rental charge per space and the number of spaces rented must both be nonnegative quantities.)
(b) What do the slope, the y-intercept, and the x-intercept of die graph represent?

(a)

Expert Solution

To determine

To sketch: the graph of the given linear equation.

Explanation of Solution

The linear equation is given,

y=200−4x (1)

Where,

y is the number of spaces that manager can rent.

x is the charges for a rental space in dollars.

Calculate x-intercept and y-intercept of line to find the two points of the linear equation that represents a line,

Substitute 0 for y in equation (1) to find the value of x-intercept,

0=200−4x4x=200x=2004=50

The first point on the linear equation is (50,0) .

Substitute 0 for x in equation (1) to find the value of y-intercept,

y=200−4⋅0y=200−0=200

The second point on the linear equation is (0,200) .

The equation (1) is in the form of general equation y=mx+b , so the value of slope m is −4 .

Sketch the graph by the points (50,0) , (0,200) and the slope m is −4 .

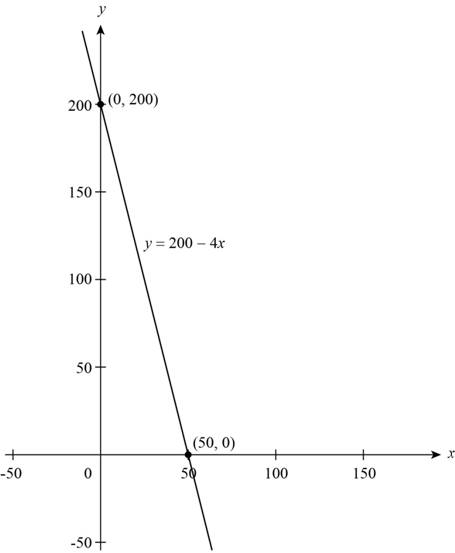
Precalculus - A Custom Text for UNLV, Chapter 1.10, Problem 68E

Figure (1)

The graph of linear equation (1) is shown in above Figure (1).

(b)

Expert Solution

To determine

The significance of slope and the y- intercept of the graph of the line.

Explanation of Solution

From part (a), the slope of the linear equation is −4 and the x- intercept is 50 and the y-intercept is 200.

The slope represents a decrease of 4 spaces rented for each one dollar increase in rental price, the y-intercept indicates that 200 spaces are rented if there is no increase in price, and the x-intercept indicates that no space are rented with an increase of $50 in rental price.

Chapter 1.10, Problem 67E

Chapter 1.10, Problem 69E

Chapter 1 Solutions

Precalculus - A Custom Text for UNLV

Ch. 1.1 - Give an example of each of the following: (a) A...Ch. 1.1 - Complete each statement and name the property of...Ch. 1.1 - Prob. 3E Ch. 1.1 - The symbol | x | stands for the __________of the...Ch. 1.1 - Prob. 5E Ch. 1.1 - Prob. 6E Ch. 1.1 - Prob. 7E Ch. 1.1 - Prob. 8E Ch. 1.1 - Prob. 9E Ch. 1.1 - Prob. 10E

Ch. 1.1 - Prob. 11E Ch. 1.1 - Prob. 12E Ch. 1.1 - Prob. 13E Ch. 1.1 - Prob. 14E Ch. 1.1 - Prob. 15E Ch. 1.1 - Prob. 16E Ch. 1.1 - Prob. 17E Ch. 1.1 - Prob. 18E Ch. 1.1 - Prob. 19E Ch. 1.1 - Prob. 20E Ch. 1.1 - Prob. 21E Ch. 1.1 - Prob. 22E Ch. 1.1 - Prob. 23E Ch. 1.1 - Prob. 24E Ch. 1.1 - Prob. 25E Ch. 1.1 - Prob. 26E Ch. 1.1 - Prob. 27E Ch. 1.1 - Prob. 28E Ch. 1.1 - Prob. 29E Ch. 1.1 - Prob. 30E Ch. 1.1 - Prob. 31E Ch. 1.1 - Prob. 32E Ch. 1.1 - Prob. 33E Ch. 1.1 - Prob. 34E Ch. 1.1 - Prob. 35E Ch. 1.1 - Prob. 36E Ch. 1.1 - Prob. 37E Ch. 1.1 - Prob. 38E Ch. 1.1 - Prob. 39E Ch. 1.1 - Prob. 40E Ch. 1.1 - Prob. 41E Ch. 1.1 - Prob. 42E Ch. 1.1 - Prob. 43E Ch. 1.1 - Prob. 44E Ch. 1.1 - Prob. 45E Ch. 1.1 - Prob. 46E Ch. 1.1 - Prob. 47E Ch. 1.1 - Prob. 48E Ch. 1.1 - Prob. 49E Ch. 1.1 - Prob. 50E Ch. 1.1 - Prob. 51E Ch. 1.1 - Prob. 52E Ch. 1.1 - Prob. 53E Ch. 1.1 - Prob. 54E Ch. 1.1 - Prob. 55E Ch. 1.1 - Prob. 56E Ch. 1.1 - Prob. 57E Ch. 1.1 - Prob. 58E Ch. 1.1 - Prob. 59E Ch. 1.1 - Prob. 60E Ch. 1.1 - Prob. 61E Ch. 1.1 - Prob. 62E Ch. 1.1 - Prob. 63E Ch. 1.1 - Prob. 64E Ch. 1.1 - Prob. 65E Ch. 1.1 - Prob. 66E Ch. 1.1 - Prob. 67E Ch. 1.1 - Prob. 68E Ch. 1.1 - Prob. 69E Ch. 1.1 - Prob. 70E Ch. 1.1 - Prob. 71E Ch. 1.1 - Prob. 72E Ch. 1.1 - Prob. 73E Ch. 1.1 - Prob. 74E Ch. 1.1 - Prob. 75E Ch. 1.1 - Prob. 76E Ch. 1.1 - Area of a Garden Marys backyard vegetable garden...Ch. 1.1 - Temperature Variation The bar graph shows the...Ch. 1.1 - Mailing a Package The post office will accept only...Ch. 1.1 - Prob. 80E Ch. 1.1 - Prob. 81E Ch. 1.1 - Prob. 82E Ch. 1.1 - Prob. 83E Ch. 1.1 - Prob. 84E Ch. 1.1 - Prob. 85E Ch. 1.2 - (a) Using exponential notation, we can write the...Ch. 1.2 - (a) When we multiply two powers with the same...Ch. 1.2 - Prob. 3E Ch. 1.2 - Explain what 43/2 means, then calculate 43/2 in...Ch. 1.2 - Explain how we rationalize a denominator, then...Ch. 1.2 - Find the missing power in the following...Ch. 1.2 - Prob. 7E Ch. 1.2 - Prob. 8E Ch. 1.2 - Prob. 9E Ch. 1.2 - Prob. 10E Ch. 1.2 - Prob. 11E Ch. 1.2 - Prob. 12E Ch. 1.2 - Prob. 13E Ch. 1.2 - Prob. 14E Ch. 1.2 - Prob. 15E Ch. 1.2 - Prob. 16E Ch. 1.2 - Prob. 17E Ch. 1.2 - Prob. 18E Ch. 1.2 - Prob. 19E Ch. 1.2 - Prob. 20E Ch. 1.2 - Prob. 21E Ch. 1.2 - Prob. 22E Ch. 1.2 - Prob. 23E Ch. 1.2 - Prob. 24E Ch. 1.2 - Prob. 25E Ch. 1.2 - Prob. 26E Ch. 1.2 - Prob. 27E Ch. 1.2 - Prob. 28E Ch. 1.2 - Prob. 29E Ch. 1.2 - Prob. 30E Ch. 1.2 - Prob. 31E Ch. 1.2 - Prob. 32E Ch. 1.2 - Prob. 33E Ch. 1.2 - Prob. 34E Ch. 1.2 - Prob. 35E Ch. 1.2 - Prob. 36E Ch. 1.2 - Prob. 37E Ch. 1.2 - Prob. 38E Ch. 1.2 - Prob. 39E Ch. 1.2 - Prob. 40E Ch. 1.2 - Prob. 41E Ch. 1.2 - Prob. 42E Ch. 1.2 - Prob. 43E Ch. 1.2 - Prob. 44E Ch. 1.2 - Prob. 45E Ch. 1.2 - Prob. 46E Ch. 1.2 - Prob. 47E Ch. 1.2 - Prob. 48E Ch. 1.2 - Prob. 49E Ch. 1.2 - Prob. 50E Ch. 1.2 - Prob. 51E Ch. 1.2 - Prob. 52E Ch. 1.2 - Prob. 53E Ch. 1.2 - Prob. 54E Ch. 1.2 - Prob. 55E Ch. 1.2 - Prob. 56E Ch. 1.2 - Prob. 57E Ch. 1.2 - Prob. 58E Ch. 1.2 - Prob. 59E Ch. 1.2 - Prob. 60E Ch. 1.2 - Prob. 61E Ch. 1.2 - Prob. 62E Ch. 1.2 - Prob. 63E Ch. 1.2 - Prob. 64E Ch. 1.2 - Prob. 65E Ch. 1.2 - Prob. 66E Ch. 1.2 - Prob. 67E Ch. 1.2 - Prob. 68E Ch. 1.2 - Prob. 69E Ch. 1.2 - Prob. 70E Ch. 1.2 - Prob. 71E Ch. 1.2 - Prob. 72E Ch. 1.2 - Prob. 73E Ch. 1.2 - Prob. 74E Ch. 1.2 - Prob. 75E Ch. 1.2 - Prob. 76E Ch. 1.2 - Prob. 77E Ch. 1.2 - Prob. 78E Ch. 1.2 - Prob. 79E Ch. 1.2 - Prob. 80E Ch. 1.2 - Prob. 81E Ch. 1.2 - Prob. 82E Ch. 1.2 - Prob. 83E Ch. 1.2 - Prob. 84E Ch. 1.2 - Prob. 85E Ch. 1.2 - Prob. 86E Ch. 1.2 - Prob. 87E Ch. 1.2 - Prob. 88E Ch. 1.2 - Prob. 89E Ch. 1.2 - Prob. 90E Ch. 1.2 - Prob. 91E Ch. 1.2 - Prob. 92E Ch. 1.2 - Prob. 93E Ch. 1.2 - Prob. 94E Ch. 1.2 - Prob. 95E Ch. 1.2 - Prob. 96E Ch. 1.2 - Volume of the Oceans The average ocean depth is...Ch. 1.2 - Prob. 98E Ch. 1.2 - Number of Molecules A sealed room in a hospital,...Ch. 1.2 - Prob. 100E Ch. 1.2 - Speed of a Skidding Car Police use the formula...Ch. 1.2 - Distance from the Earth to the Sun It follows from...Ch. 1.2 - Prob. 103E Ch. 1.2 - Prob. 104E Ch. 1.2 - Prob. 105E Ch. 1.2 - Prob. 106E Ch. 1.3 - Prob. 1E Ch. 1.3 - To factor the trinomial x2 + 7x + 10, we look for...Ch. 1.3 - The Special Product Formula for the square of a...Ch. 1.3 - The Special Product Formula for the product of the...Ch. 1.3 - Prob. 5E Ch. 1.3 - Prob. 6E Ch. 1.3 - Prob. 7E Ch. 1.3 - Prob. 8E Ch. 1.3 - Prob. 9E Ch. 1.3 - Prob. 10E Ch. 1.3 - Prob. 11E Ch. 1.3 - Prob. 12E Ch. 1.3 - Prob. 13E Ch. 1.3 - Prob. 14E Ch. 1.3 - Prob. 15E Ch. 1.3 - Prob. 16E Ch. 1.3 - Prob. 17E Ch. 1.3 - Prob. 18E Ch. 1.3 - Prob. 19E Ch. 1.3 - Prob. 20E Ch. 1.3 - Prob. 21E Ch. 1.3 - Prob. 22E Ch. 1.3 - Prob. 23E Ch. 1.3 - Prob. 24E Ch. 1.3 - Prob. 25E Ch. 1.3 - Prob. 26E Ch. 1.3 - Prob. 27E Ch. 1.3 - Prob. 28E Ch. 1.3 - Prob. 29E Ch. 1.3 - Prob. 30E Ch. 1.3 - Prob. 31E Ch. 1.3 - Prob. 32E Ch. 1.3 - Prob. 33E Ch. 1.3 - Prob. 34E Ch. 1.3 - Prob. 35E Ch. 1.3 - Prob. 36E Ch. 1.3 - Prob. 37E Ch. 1.3 - Prob. 38E Ch. 1.3 - Prob. 39E Ch. 1.3 - Prob. 40E Ch. 1.3 - Prob. 41E Ch. 1.3 - Prob. 42E Ch. 1.3 - Prob. 43E Ch. 1.3 - Prob. 44E Ch. 1.3 - Prob. 45E Ch. 1.3 - Prob. 46E Ch. 1.3 - Prob. 47E Ch. 1.3 - Prob. 48E Ch. 1.3 - Prob. 49E Ch. 1.3 - Prob. 50E Ch. 1.3 - Prob. 51E Ch. 1.3 - Prob. 52E Ch. 1.3 - Prob. 53E Ch. 1.3 - Prob. 54E Ch. 1.3 - Prob. 55E Ch. 1.3 - Prob. 56E Ch. 1.3 - Prob. 57E Ch. 1.3 - Prob. 58E Ch. 1.3 - Prob. 59E Ch. 1.3 - Prob. 60E Ch. 1.3 - Prob. 61E Ch. 1.3 - Prob. 62E Ch. 1.3 - Prob. 63E Ch. 1.3 - Prob. 64E Ch. 1.3 - Prob. 65E Ch. 1.3 - Prob. 66E Ch. 1.3 - Prob. 67E Ch. 1.3 - Prob. 68E Ch. 1.3 - Prob. 69E Ch. 1.3 - Prob. 70E Ch. 1.3 - Prob. 71E Ch. 1.3 - Prob. 72E Ch. 1.3 - Prob. 73E Ch. 1.3 - Prob. 74E Ch. 1.3 - Prob. 75E Ch. 1.3 - Prob. 76E Ch. 1.3 - Prob. 77E Ch. 1.3 - Prob. 78E Ch. 1.3 - Prob. 79E Ch. 1.3 - Prob. 80E Ch. 1.3 - Prob. 81E Ch. 1.3 - Prob. 82E Ch. 1.3 - Prob. 83E Ch. 1.3 - Prob. 84E Ch. 1.3 - Prob. 85E Ch. 1.3 - Prob. 86E Ch. 1.3 - Prob. 87E Ch. 1.3 - Prob. 88E Ch. 1.3 - Prob. 89E Ch. 1.3 - Prob. 90E Ch. 1.3 - Prob. 91E Ch. 1.3 - Prob. 92E Ch. 1.3 - Prob. 93E Ch. 1.3 - Prob. 94E Ch. 1.3 - Prob. 95E Ch. 1.3 - Prob. 96E Ch. 1.3 - Prob. 97E Ch. 1.3 - Prob. 98E Ch. 1.3 - Prob. 99E Ch. 1.3 - Prob. 100E Ch. 1.3 - Prob. 101E Ch. 1.3 - Prob. 102E Ch. 1.3 - Prob. 103E Ch. 1.3 - Prob. 104E Ch. 1.3 - Prob. 105E Ch. 1.3 - Prob. 106E Ch. 1.3 - Prob. 107E Ch. 1.3 - Prob. 108E Ch. 1.3 - Prob. 109E Ch. 1.3 - Prob. 110E Ch. 1.3 - Prob. 111E Ch. 1.3 - Prob. 112E Ch. 1.3 - Prob. 113E Ch. 1.3 - Prob. 114E Ch. 1.3 - Prob. 115E Ch. 1.3 - Prob. 116E Ch. 1.3 - Prob. 117E Ch. 1.3 - Prob. 118E Ch. 1.3 - Prob. 119E Ch. 1.3 - Prob. 120E Ch. 1.3 - Prob. 121E Ch. 1.3 - Prob. 122E Ch. 1.3 - Prob. 123E Ch. 1.3 - Prob. 124E Ch. 1.3 - Prob. 125E Ch. 1.3 - Prob. 126E Ch. 1.3 - Prob. 127E Ch. 1.3 - Prob. 128E Ch. 1.3 - Prob. 129E Ch. 1.3 - Prob. 130E Ch. 1.3 - Prob. 131E Ch. 1.3 - Prob. 132E Ch. 1.3 - Prob. 133E Ch. 1.3 - Prob. 134E Ch. 1.3 - Prob. 135E Ch. 1.3 - Prob. 136E Ch. 1.3 - Prob. 137E Ch. 1.4 - Which of the following are rational expressions?...Ch. 1.4 - To simplify a rational expression, we cancel...Ch. 1.4 - Prob. 3E Ch. 1.4 - Prob. 4E Ch. 1.4 - Prob. 5E Ch. 1.4 - Prob. 6E Ch. 1.4 - Prob. 7E Ch. 1.4 - Prob. 8E Ch. 1.4 - Prob. 9E Ch. 1.4 - Prob. 10E Ch. 1.4 - Prob. 11E Ch. 1.4 - Prob. 12E Ch. 1.4 - Prob. 13E Ch. 1.4 - Prob. 14E Ch. 1.4 - Prob. 15E Ch. 1.4 - Prob. 16E Ch. 1.4 - Prob. 17E Ch. 1.4 - Prob. 18E Ch. 1.4 - Prob. 19E Ch. 1.4 - Prob. 20E Ch. 1.4 - Prob. 21E Ch. 1.4 - Prob. 22E Ch. 1.4 - Prob. 23E Ch. 1.4 - Prob. 24E Ch. 1.4 - Prob. 25E Ch. 1.4 - Prob. 26E Ch. 1.4 - Prob. 27E Ch. 1.4 - Prob. 28E Ch. 1.4 - Prob. 29E Ch. 1.4 - Prob. 30E Ch. 1.4 - Prob. 31E Ch. 1.4 - Prob. 32E Ch. 1.4 - Prob. 33E Ch. 1.4 - Prob. 34E Ch. 1.4 - Prob. 35E Ch. 1.4 - Prob. 36E Ch. 1.4 - Prob. 37E Ch. 1.4 - Prob. 38E Ch. 1.4 - Prob. 39E Ch. 1.4 - Prob. 40E Ch. 1.4 - Prob. 41E Ch. 1.4 - Prob. 42E Ch. 1.4 - Prob. 43E Ch. 1.4 - Prob. 44E Ch. 1.4 - Prob. 45E Ch. 1.4 - Prob. 46E Ch. 1.4 - Prob. 47E Ch. 1.4 - Prob. 48E Ch. 1.4 - Prob. 49E Ch. 1.4 - Prob. 50E Ch. 1.4 - Prob. 51E Ch. 1.4 - Prob. 52E Ch. 1.4 - Prob. 53E Ch. 1.4 - Prob. 54E Ch. 1.4 - Prob. 55E Ch. 1.4 - Prob. 56E Ch. 1.4 - Prob. 57E Ch. 1.4 - Prob. 58E Ch. 1.4 - Prob. 59E Ch. 1.4 - Prob. 60E Ch. 1.4 - Prob. 61E Ch. 1.4 - Prob. 62E Ch. 1.4 - Prob. 63E Ch. 1.4 - Prob. 64E Ch. 1.4 - Prob. 65E Ch. 1.4 - Prob. 66E Ch. 1.4 - Prob. 67E Ch. 1.4 - Prob. 68E Ch. 1.4 - Prob. 69E Ch. 1.4 - Prob. 70E Ch. 1.4 - Prob. 71E Ch. 1.4 - Prob. 72E Ch. 1.4 - Prob. 73E Ch. 1.4 - Prob. 74E Ch. 1.4 - Prob. 75E Ch. 1.4 - Prob. 76E Ch. 1.4 - Prob. 77E Ch. 1.4 - Prob. 78E Ch. 1.4 - Prob. 79E Ch. 1.4 - Prob. 80E Ch. 1.4 - Prob. 81E Ch. 1.4 - Prob. 82E Ch. 1.4 - Prob. 83E Ch. 1.4 - Prob. 84E Ch. 1.4 - Prob. 85E Ch. 1.4 - Prob. 86E Ch. 1.4 - Prob. 87E Ch. 1.4 - Prob. 88E Ch. 1.4 - Prob. 89E Ch. 1.4 - Prob. 90E Ch. 1.4 - Prob. 91E Ch. 1.4 - Prob. 92E Ch. 1.4 - Prob. 93E Ch. 1.4 - Prob. 94E Ch. 1.4 - Prob. 95E Ch. 1.4 - Prob. 96E Ch. 1.4 - Prob. 97E Ch. 1.4 - Prob. 98E Ch. 1.4 - Prob. 99E Ch. 1.4 - Prob. 100E Ch. 1.4 - Prob. 101E Ch. 1.4 - Average Cost A clothing manufacturer finds that...Ch. 1.4 - Prob. 103E Ch. 1.4 - Prob. 104E Ch. 1.4 - Prob. 105E Ch. 1.4 - Prob. 106E Ch. 1.5 - Prob. 1E Ch. 1.5 - Explain how you would use each method to solve the...Ch. 1.5 - Prob. 3E Ch. 1.5 - Prob. 4E Ch. 1.5 - The equation (x + 1)2 5(x + 1) + 6 = 0 is...Ch. 1.5 - Prob. 6E Ch. 1.5 - Prob. 7E Ch. 1.5 - Prob. 8E Ch. 1.5 - Prob. 9E Ch. 1.5 - Prob. 10E Ch. 1.5 - Prob. 11E Ch. 1.5 - Prob. 12E Ch. 1.5 - Prob. 13E Ch. 1.5 - Prob. 14E Ch. 1.5 - Prob. 15E Ch. 1.5 - Prob. 16E Ch. 1.5 - Prob. 17E Ch. 1.5 - Prob. 18E Ch. 1.5 - Prob. 19E Ch. 1.5 - Prob. 20E Ch. 1.5 - Prob. 21E Ch. 1.5 - Prob. 22E Ch. 1.5 - Prob. 23E Ch. 1.5 - Prob. 24E Ch. 1.5 - Prob. 25E Ch. 1.5 - Prob. 26E Ch. 1.5 - Prob. 27E Ch. 1.5 - Prob. 28E Ch. 1.5 - Prob. 29E Ch. 1.5 - Prob. 30E Ch. 1.5 - Prob. 31E Ch. 1.5 - Prob. 32E Ch. 1.5 - Prob. 33E Ch. 1.5 - Prob. 34E Ch. 1.5 - Prob. 35E Ch. 1.5 - Prob. 36E Ch. 1.5 - Prob. 37E Ch. 1.5 - Prob. 38E Ch. 1.5 - Prob. 39E Ch. 1.5 - Prob. 40E Ch. 1.5 - Prob. 41E Ch. 1.5 - Prob. 42E Ch. 1.5 - Prob. 43E Ch. 1.5 - Prob. 44E Ch. 1.5 - Prob. 45E Ch. 1.5 - Prob. 46E Ch. 1.5 - Prob. 47E Ch. 1.5 - Prob. 48E Ch. 1.5 - Prob. 49E Ch. 1.5 - Prob. 50E Ch. 1.5 - Prob. 51E Ch. 1.5 - Prob. 52E Ch. 1.5 - Prob. 53E Ch. 1.5 - Prob. 54E Ch. 1.5 - Prob. 55E Ch. 1.5 - Prob. 56E Ch. 1.5 - Prob. 57E Ch. 1.5 - Prob. 58E Ch. 1.5 - Prob. 59E Ch. 1.5 - Prob. 60E Ch. 1.5 - Prob. 61E Ch. 1.5 - Prob. 62E Ch. 1.5 - Prob. 63E Ch. 1.5 - Prob. 64E Ch. 1.5 - Prob. 65E Ch. 1.5 - Prob. 66E Ch. 1.5 - Prob. 67E Ch. 1.5 - Prob. 68E Ch. 1.5 - Prob. 69E Ch. 1.5 - Prob. 70E Ch. 1.5 - Prob. 71E Ch. 1.5 - Prob. 72E Ch. 1.5 - Prob. 73E Ch. 1.5 - Prob. 74E Ch. 1.5 - Prob. 75E Ch. 1.5 - Prob. 76E Ch. 1.5 - Prob. 77E Ch. 1.5 - Prob. 78E Ch. 1.5 - Prob. 79E Ch. 1.5 - Prob. 80E Ch. 1.5 - Prob. 81E Ch. 1.5 - Prob. 82E Ch. 1.5 - Prob. 83E Ch. 1.5 - Prob. 84E Ch. 1.5 - Prob. 85E Ch. 1.5 - Prob. 86E Ch. 1.5 - Prob. 87E Ch. 1.5 - Prob. 88E Ch. 1.5 - Prob. 89E Ch. 1.5 - Prob. 90E Ch. 1.5 - Prob. 91E Ch. 1.5 - Prob. 92E Ch. 1.5 - Prob. 93E Ch. 1.5 - Prob. 94E Ch. 1.5 - Prob. 95E Ch. 1.5 - Prob. 96E Ch. 1.5 - Prob. 97E Ch. 1.5 - Prob. 98E Ch. 1.5 - Prob. 99E Ch. 1.5 - Prob. 100E Ch. 1.5 - Prob. 101E Ch. 1.5 - Prob. 102E Ch. 1.5 - Prob. 103E Ch. 1.5 - Prob. 104E Ch. 1.5 - Prob. 105E Ch. 1.5 - Prob. 106E Ch. 1.5 - Prob. 107E Ch. 1.5 - Prob. 108E Ch. 1.5 - Falling-Body Problems Suppose an object is dropped...Ch. 1.5 - Falling-Body Problems Suppose an object is dropped...Ch. 1.5 - Falling-Body Problems Use the formula h = 16t2 +...Ch. 1.5 - Prob. 112E Ch. 1.5 - Shrinkage in Concrete Beams As concrete dries, it...Ch. 1.5 - The Lens Equation If F is the focal length of a...Ch. 1.5 - Fish Population The fish population in a certain...Ch. 1.5 - Fish Population A large pond is stocked with fish....Ch. 1.5 - Profit A small-appliance manufacturer finds that...Ch. 1.5 - Gravity If an imaginary line segment is drawn...Ch. 1.5 - Depth of a Well One method for determining the...Ch. 1.5 - Prob. 120E Ch. 1.5 - Prob. 121E Ch. 1.5 - Prob. 122E Ch. 1.5 - Prob. 123E Ch. 1.5 - Prob. 124E Ch. 1.6 - Explain in your own words what it means for an...Ch. 1.6 - In the formula I = Prt for simple interest. P...Ch. 1.6 - Prob. 3E Ch. 1.6 - Balsamic vinegar contains 5% acetic acid, so a...Ch. 1.6 - Prob. 5E Ch. 1.6 - The formula d = rt models the distance d traveled...Ch. 1.6 - Prob. 7E Ch. 1.6 - Prob. 8E Ch. 1.6 - Prob. 9E Ch. 1.6 - Prob. 10E Ch. 1.6 - Prob. 11E Ch. 1.6 - Prob. 12E Ch. 1.6 - Prob. 13E Ch. 1.6 - Prob. 14E Ch. 1.6 - Prob. 15E Ch. 1.6 - Prob. 16E Ch. 1.6 - Prob. 17E Ch. 1.6 - Prob. 18E Ch. 1.6 - Prob. 19E Ch. 1.6 - Cell Phone Costs A cell phone company charges a...Ch. 1.6 - Investments Phyllis invested 12,000, a portion...Ch. 1.6 - Investments If Ben invests 4000 at 4% interest per...Ch. 1.6 - Prob. 23E Ch. 1.6 - Prob. 24E Ch. 1.6 - Salaries An executive in an engineering firm earns...Ch. 1.6 - Prob. 26E Ch. 1.6 - Prob. 27E Ch. 1.6 - Overtime Pay Helen earns 7.50 an hour at her job,...Ch. 1.6 - Prob. 29E Ch. 1.6 - Prob. 30E Ch. 1.6 - A Riddle A movie star, unwilling to give his age,...Ch. 1.6 - Career Home Runs During his major league career,...Ch. 1.6 - Value of Coins A change purse contains an equal...Ch. 1.6 - Value of Coins Mary has 3.00 in nickels, dimes,...Ch. 1.6 - Length of a Garden A rectangular garden is 25 ft...Ch. 1.6 - Prob. 36E Ch. 1.6 - Dimensions of a Lot A square plot of land has a...Ch. 1.6 - Prob. 38E Ch. 1.6 - Dimensions of a Garden A rectangular garden is 10...Ch. 1.6 - Prob. 40E Ch. 1.6 - Prob. 41E Ch. 1.6 - Prob. 42E Ch. 1.6 - Dimensions of a Lot A rectangular parcel of land...Ch. 1.6 - Dimensions of a Track A running track has the...Ch. 1.6 - Prob. 45E Ch. 1.6 - Prob. 46E Ch. 1.6 - Framing a Painting Ali paints with watercolors on...Ch. 1.6 - Dimensions of a Poster A poster has a rectangular...Ch. 1.6 - Prob. 49E Ch. 1.6 - Prob. 50E Ch. 1.6 - Length of a Shadow A man is walking away from a...Ch. 1.6 - Height of a Tree A woodcutter determines the...Ch. 1.6 - Prob. 53E Ch. 1.6 - Mixture Problem What amount of pure acid must be...Ch. 1.6 - Mixture Problem A jeweler has five rings, each...Ch. 1.6 - Mixture Problem A pot contains 6 L of brine at a...Ch. 1.6 - Mixture Problem The radiator in a car is filled...Ch. 1.6 - Prob. 58E Ch. 1.6 - Mixture Problem A bottle contains 750 mL of fruit...Ch. 1.6 - Mixture Problem A merchant blends tea that sells...Ch. 1.6 - Sharing a Job Candy and Tim share a paper route....Ch. 1.6 - Prob. 62E Ch. 1.6 - Sharing a Job Betty and Karen have been hired to...Ch. 1.6 - Sharing a Job Next-door neighbors Bob and Jim use...Ch. 1.6 - Sharing a Job Henry and Irene working together can...Ch. 1.6 - Sharing a Job Jack, Kay, and Lynn deliver...Ch. 1.6 - Distance, Speed, and Time Wendy took a trip from...Ch. 1.6 - Distance, Speed, and Time Two cyclists, 90 mi...Ch. 1.6 - Distance, Speed, and Time A pilot flew a jet from...Ch. 1.6 - Distance, Speed, and Time A woman driving a car 14...Ch. 1.6 - Distance, Speed, and Time A salesman drives from...Ch. 1.6 - Distance, Speed, and Time Kiran drove from Tortula...Ch. 1.6 - Distance, Speed, and Time It took a crew 2 h 40...Ch. 1.6 - Speed of a Boat Two fishing boats depart a harbor...Ch. 1.6 - Law of the Lever The figure shows a lever system,...Ch. 1.6 - Law of the Lever A plank 30 ft long rests on top...Ch. 1.6 - Dimensions of a Box A large plywood box has a...Ch. 1.6 - Prob. 78E Ch. 1.6 - Prob. 79E Ch. 1.6 - Prob. 80E Ch. 1.6 - Prob. 81E Ch. 1.6 - Dimensions of a Lot A city lot has the shape of a...Ch. 1.6 - Construction Costs The town of Foxton lies 10 mi...Ch. 1.6 - Distance, Speed, and Time A boardwalk is parallel...Ch. 1.6 - Volume of Grain Grain is falling from a chute onto...Ch. 1.6 - Prob. 86E Ch. 1.6 - Prob. 87E Ch. 1.6 - Prob. 88E Ch. 1.6 - An Ancient Chinese Problem This problem is taken...Ch. 1.6 - Prob. 90E Ch. 1.6 - Prob. 91E Ch. 1.7 - Fill in the blank with an appropriate inequality...Ch. 1.7 - Prob. 2E Ch. 1.7 - Prob. 3E Ch. 1.7 - (a) The set of all points on the real line whose...Ch. 1.7 - Prob. 5E Ch. 1.7 - Prob. 6E Ch. 1.7 - Prob. 7E Ch. 1.7 - Prob. 8E Ch. 1.7 - Prob. 9E Ch. 1.7 - Prob. 10E Ch. 1.7 - Prob. 11E Ch. 1.7 - Prob. 12E Ch. 1.7 - Prob. 13E Ch. 1.7 - Prob. 14E Ch. 1.7 - Prob. 15E Ch. 1.7 - Prob. 16E Ch. 1.7 - Prob. 17E Ch. 1.7 - Prob. 18E Ch. 1.7 - Prob. 19E Ch. 1.7 - Prob. 20E Ch. 1.7 - Prob. 21E Ch. 1.7 - Prob. 22E Ch. 1.7 - Prob. 23E Ch. 1.7 - Prob. 24E Ch. 1.7 - Prob. 25E Ch. 1.7 - Prob. 26E Ch. 1.7 - Prob. 27E Ch. 1.7 - Prob. 28E Ch. 1.7 - Prob. 29E Ch. 1.7 - Prob. 30E Ch. 1.7 - Prob. 31E Ch. 1.7 - Prob. 32E Ch. 1.7 - Prob. 33E Ch. 1.7 - Prob. 34E Ch. 1.7 - Prob. 35E Ch. 1.7 - Prob. 36E Ch. 1.7 - Prob. 37E Ch. 1.7 - Prob. 38E Ch. 1.7 - Prob. 39E Ch. 1.7 - Prob. 40E Ch. 1.7 - Prob. 41E Ch. 1.7 - Prob. 42E Ch. 1.7 - Prob. 43E Ch. 1.7 - Prob. 44E Ch. 1.7 - Prob. 45E Ch. 1.7 - Prob. 46E Ch. 1.7 - Prob. 47E Ch. 1.7 - Prob. 48E Ch. 1.7 - Prob. 49E Ch. 1.7 - Prob. 50E Ch. 1.7 - Prob. 51E Ch. 1.7 - Prob. 52E Ch. 1.7 - Prob. 53E Ch. 1.7 - Prob. 54E Ch. 1.7 - Prob. 55E Ch. 1.7 - Prob. 56E Ch. 1.7 - Prob. 57E Ch. 1.7 - Prob. 58E Ch. 1.7 - Prob. 59E Ch. 1.7 - Prob. 60E Ch. 1.7 - Prob. 61E Ch. 1.7 - Prob. 62E Ch. 1.7 - Prob. 63E Ch. 1.7 - Prob. 64E Ch. 1.7 - Prob. 65E Ch. 1.7 - Prob. 66E Ch. 1.7 - Prob. 67E Ch. 1.7 - Prob. 68E Ch. 1.7 - Prob. 69E Ch. 1.7 - Prob. 70E Ch. 1.7 - Prob. 71E Ch. 1.7 - Prob. 72E Ch. 1.7 - Prob. 73E Ch. 1.7 - Prob. 74E Ch. 1.7 - Prob. 75E Ch. 1.7 - Prob. 76E Ch. 1.7 - Prob. 77E Ch. 1.7 - Prob. 78E Ch. 1.7 - Prob. 79E Ch. 1.7 - Prob. 80E Ch. 1.7 - Prob. 81E Ch. 1.7 - Prob. 82E Ch. 1.7 - Prob. 83E Ch. 1.7 - Prob. 84E Ch. 1.7 - Prob. 85E Ch. 1.7 - Prob. 86E Ch. 1.7 - Prob. 87E Ch. 1.7 - Prob. 88E Ch. 1.7 - Prob. 89E Ch. 1.7 - Prob. 90E Ch. 1.7 - Prob. 91E Ch. 1.7 - Prob. 92E Ch. 1.7 - Prob. 93E Ch. 1.7 - Prob. 94E Ch. 1.7 - Prob. 95E Ch. 1.7 - Prob. 96E Ch. 1.7 - Prob. 97E Ch. 1.7 - Prob. 98E Ch. 1.7 - Prob. 99E Ch. 1.7 - Prob. 100E Ch. 1.7 - Prob. 101E Ch. 1.7 - Prob. 102E Ch. 1.7 - Prob. 103E Ch. 1.7 - Prob. 104E Ch. 1.7 - Prob. 105E Ch. 1.7 - Temperature Scales What interval on the Celsius...Ch. 1.7 - Prob. 107E Ch. 1.7 - International Plans A phone service provider...Ch. 1.7 - Driving Cost It is estimated that the annual cost...Ch. 1.7 - Air Temperature As dry air moves upward, it...Ch. 1.7 - Airline Ticket Price A charter airline finds that...Ch. 1.7 - Accuracy of a Scale A coffee merchant sells a...Ch. 1.7 - Prob. 113E Ch. 1.7 - Bonfire Temperature In the vicinity of a bonfire...Ch. 1.7 - Falling Ball Using calculus, it can be shown that...Ch. 1.7 - Gas Mileage The gas mileage g (measured in mi/gal)...Ch. 1.7 - Stopping Distance For a certain model of car the...Ch. 1.7 - Prob. 118E Ch. 1.7 - Fencing a Garden A determined gardener has 120 ft...Ch. 1.7 - Thickness of a Laminate A company manufactures...Ch. 1.7 - Range of Height The average height of adult males...Ch. 1.7 - Prob. 122E Ch. 1.7 - Prob. 123E Ch. 1.7 - Prob. 124E Ch. 1.8 - The point that is 3 units to the right of the...Ch. 1.8 - Prob. 2E Ch. 1.8 - The point midway between (a, b) and (c, d) is...Ch. 1.8 - Prob. 4E Ch. 1.8 - Prob. 5E Ch. 1.8 - Prob. 6E Ch. 1.8 - Prob. 7E Ch. 1.8 - Prob. 8E Ch. 1.8 - Prob. 9E Ch. 1.8 - Prob. 10E Ch. 1.8 - Prob. 11E Ch. 1.8 - Prob. 12E Ch. 1.8 - Prob. 13E Ch. 1.8 - Prob. 14E Ch. 1.8 - Prob. 15E Ch. 1.8 - Prob. 16E Ch. 1.8 - Prob. 17E Ch. 1.8 - Prob. 18E Ch. 1.8 - Prob. 19E Ch. 1.8 - Prob. 20E Ch. 1.8 - Prob. 21E Ch. 1.8 - Prob. 22E Ch. 1.8 - Prob. 23E Ch. 1.8 - Prob. 24E Ch. 1.8 - Prob. 25E Ch. 1.8 - Prob. 26E Ch. 1.8 - Prob. 27E Ch. 1.8 - Prob. 28E Ch. 1.8 - Prob. 29E Ch. 1.8 - Prob. 30E Ch. 1.8 - Prob. 31E Ch. 1.8 - Prob. 32E Ch. 1.8 - Prob. 33E Ch. 1.8 - Prob. 34E Ch. 1.8 - Prob. 35E Ch. 1.8 - Prob. 36E Ch. 1.8 - Prob. 37E Ch. 1.8 - Prob. 38E Ch. 1.8 - Prob. 39E Ch. 1.8 - Prob. 40E Ch. 1.8 - Prob. 41E Ch. 1.8 - Prob. 42E Ch. 1.8 - Prob. 43E Ch. 1.8 - Prob. 44E Ch. 1.8 - Prob. 45E Ch. 1.8 - Prob. 46E Ch. 1.8 - Prob. 47E Ch. 1.8 - Prob. 48E Ch. 1.8 - Prob. 49E Ch. 1.8 - Prob. 50E Ch. 1.8 - Prob. 51E Ch. 1.8 - Prob. 52E Ch. 1.8 - Prob. 53E Ch. 1.8 - Prob. 54E Ch. 1.8 - Prob. 55E Ch. 1.8 - Prob. 56E Ch. 1.8 - Prob. 57E Ch. 1.8 - Prob. 58E Ch. 1.8 - Prob. 59E Ch. 1.8 - Prob. 60E Ch. 1.8 - Prob. 61E Ch. 1.8 - Prob. 62E Ch. 1.8 - Prob. 63E Ch. 1.8 - Prob. 64E Ch. 1.8 - Prob. 65E Ch. 1.8 - Prob. 66E Ch. 1.8 - Prob. 67E Ch. 1.8 - Prob. 68E Ch. 1.8 - Prob. 69E Ch. 1.8 - Prob. 70E Ch. 1.8 - Prob. 71E Ch. 1.8 - Prob. 72E Ch. 1.8 - Prob. 73E Ch. 1.8 - Prob. 74E Ch. 1.8 - Prob. 75E Ch. 1.8 - Prob. 76E Ch. 1.8 - Prob. 77E Ch. 1.8 - Prob. 78E Ch. 1.8 - Prob. 79E Ch. 1.8 - Prob. 80E Ch. 1.8 - Prob. 81E Ch. 1.8 - Prob. 82E Ch. 1.8 - Prob. 83E Ch. 1.8 - Prob. 84E Ch. 1.8 - Prob. 85E Ch. 1.8 - Prob. 86E Ch. 1.8 - Prob. 87E Ch. 1.8 - Prob. 88E Ch. 1.8 - Prob. 89E Ch. 1.8 - Prob. 90E Ch. 1.8 - Prob. 91E Ch. 1.8 - Prob. 92E Ch. 1.8 - Prob. 93E Ch. 1.8 - Prob. 94E Ch. 1.8 - Prob. 95E Ch. 1.8 - Prob. 96E Ch. 1.8 - Prob. 97E Ch. 1.8 - Prob. 98E Ch. 1.8 - Prob. 99E Ch. 1.8 - Prob. 100E Ch. 1.8 - Prob. 101E Ch. 1.8 - Prob. 102E Ch. 1.8 - Prob. 103E Ch. 1.8 - Prob. 104E Ch. 1.8 - Prob. 105E Ch. 1.8 - Prob. 106E Ch. 1.8 - Prob. 107E Ch. 1.8 - Prob. 108E Ch. 1.8 - Prob. 109E Ch. 1.8 - Prob. 110E Ch. 1.8 - Prob. 111E Ch. 1.8 - Prob. 112E Ch. 1.8 - Distances in a City A city has streets that run...Ch. 1.8 - Halfway Point Two friends live in the city...Ch. 1.8 - Orbit of a Satellite A satellite is in orbit...Ch. 1.8 - Prob. 116E Ch. 1.8 - Prob. 117E Ch. 1.8 - Prob. 118E Ch. 1.8 - Prob. 119E Ch. 1.8 - Prob. 120E Ch. 1.8 - Prob. 121E Ch. 1.8 - Prob. 122E Ch. 1.9 - Prob. 1E Ch. 1.9 - Prob. 2E Ch. 1.9 - Prob. 3E Ch. 1.9 - Prob. 4E Ch. 1.9 - Prob. 5E Ch. 1.9 - Prob. 6E Ch. 1.9 - Prob. 7E Ch. 1.9 - Prob. 8E Ch. 1.9 - Prob. 9E Ch. 1.9 - Prob. 10E Ch. 1.9 - Prob. 11E Ch. 1.9 - Prob. 12E Ch. 1.9 - Prob. 13E Ch. 1.9 - Prob. 14E Ch. 1.9 - Prob. 15E Ch. 1.9 - Prob. 16E Ch. 1.9 - Prob. 17E Ch. 1.9 - Prob. 18E Ch. 1.9 - Prob. 19E Ch. 1.9 - Prob. 20E Ch. 1.9 - Prob. 21E Ch. 1.9 - Prob. 22E Ch. 1.9 - Prob. 23E Ch. 1.9 - Prob. 24E Ch. 1.9 - Prob. 25E Ch. 1.9 - Prob. 26E Ch. 1.9 - Prob. 27E Ch. 1.9 - Prob. 28E Ch. 1.9 - Prob. 29E Ch. 1.9 - Prob. 30E Ch. 1.9 - Prob. 31E Ch. 1.9 - Prob. 32E Ch. 1.9 - Prob. 33E Ch. 1.9 - Prob. 34E Ch. 1.9 - Prob. 35E Ch. 1.9 - Prob. 36E Ch. 1.9 - Prob. 37E Ch. 1.9 - Prob. 38E Ch. 1.9 - Prob. 39E Ch. 1.9 - Prob. 40E Ch. 1.9 - Prob. 41E Ch. 1.9 - Prob. 42E Ch. 1.9 - Prob. 43E Ch. 1.9 - Prob. 44E Ch. 1.9 - Prob. 45E Ch. 1.9 - Prob. 46E Ch. 1.9 - Prob. 47E Ch. 1.9 - Prob. 48E Ch. 1.9 - Prob. 49E Ch. 1.9 - Prob. 50E Ch. 1.9 - Prob. 51E Ch. 1.9 - Prob. 52E Ch. 1.9 - Prob. 53E Ch. 1.9 - Prob. 54E Ch. 1.9 - Prob. 55E Ch. 1.9 - Prob. 56E Ch. 1.9 - Prob. 57E Ch. 1.9 - Prob. 58E Ch. 1.9 - Prob. 59E Ch. 1.9 - Prob. 60E Ch. 1.9 - Prob. 61E Ch. 1.9 - Prob. 62E Ch. 1.9 - Prob. 63E Ch. 1.9 - Prob. 64E Ch. 1.9 - Prob. 65E Ch. 1.9 - Prob. 66E Ch. 1.9 - Prob. 67E Ch. 1.9 - Prob. 68E Ch. 1.9 - Prob. 69E Ch. 1.9 - Prob. 70E Ch. 1.9 - Prob. 71E Ch. 1.9 - Prob. 72E Ch. 1.9 - Prob. 73E Ch. 1.9 - Prob. 74E Ch. 1.9 - Prob. 75E Ch. 1.9 - Prob. 76E Ch. 1.9 - Prob. 77E Ch. 1.10 - We find the steepness, or slope, of a line passing...Ch. 1.10 - Prob. 2E Ch. 1.10 - Prob. 3E Ch. 1.10 - Prob. 4E Ch. 1.10 - Prob. 5E Ch. 1.10 - Prob. 6E Ch. 1.10 - Prob. 7E Ch. 1.10 - Prob. 8E Ch. 1.10 - Prob. 9E Ch. 1.10 - Prob. 10E Ch. 1.10 - Prob. 11E Ch. 1.10 - Prob. 12E Ch. 1.10 - Prob. 13E Ch. 1.10 - Prob. 14E Ch. 1.10 - Prob. 15E Ch. 1.10 - Prob. 16E Ch. 1.10 - Prob. 17E Ch. 1.10 - Prob. 18E Ch. 1.10 - Prob. 19E Ch. 1.10 - Prob. 20E Ch. 1.10 - Prob. 21E Ch. 1.10 - Prob. 22E Ch. 1.10 - Prob. 23E Ch. 1.10 - Prob. 24E Ch. 1.10 - Prob. 25E Ch. 1.10 - Prob. 26E Ch. 1.10 - Prob. 27E Ch. 1.10 - Prob. 28E Ch. 1.10 - Prob. 29E Ch. 1.10 - Prob. 30E Ch. 1.10 - Prob. 31E Ch. 1.10 - Prob. 32E Ch. 1.10 - Prob. 33E Ch. 1.10 - Prob. 34E Ch. 1.10 - Prob. 35E Ch. 1.10 - Prob. 36E Ch. 1.10 - Prob. 37E Ch. 1.10 - Prob. 38E Ch. 1.10 - Prob. 39E Ch. 1.10 - Prob. 40E Ch. 1.10 - Prob. 41E Ch. 1.10 - Prob. 42E Ch. 1.10 - Prob. 43E Ch. 1.10 - Prob. 44E Ch. 1.10 - Prob. 45E Ch. 1.10 - Prob. 46E Ch. 1.10 - Prob. 47E Ch. 1.10 - Prob. 48E Ch. 1.10 - Prob. 49E Ch. 1.10 - Prob. 50E Ch. 1.10 - Prob. 51E Ch. 1.10 - Prob. 52E Ch. 1.10 - Prob. 53E Ch. 1.10 - Prob. 54E Ch. 1.10 - Prob. 55E Ch. 1.10 - Prob. 56E Ch. 1.10 - Prob. 57E Ch. 1.10 - Prob. 58E Ch. 1.10 - Prob. 59E Ch. 1.10 - Prob. 60E Ch. 1.10 - Prob. 61E Ch. 1.10 - Prob. 62E Ch. 1.10 - Prob. 63E Ch. 1.10 - Prob. 64E Ch. 1.10 - Prob. 65E Ch. 1.10 - Prob. 66E Ch. 1.10 - Drug Dosages If the recommended adult dosage for a...Ch. 1.10 - Flea Market The manager of a weekend flea market...Ch. 1.10 - Prob. 69E Ch. 1.10 - Prob. 70E Ch. 1.10 - Prob. 71E Ch. 1.10 - Depreciation A small business buys a computer for...Ch. 1.10 - Prob. 73E Ch. 1.10 - Prob. 74E Ch. 1.10 - Prob. 75E Ch. 1.10 - Prob. 76E Ch. 1.10 - Prob. 77E Ch. 1.10 - Prob. 78E Ch. 1.11 - If the quantities x and y are related by the...Ch. 1.11 - Prob. 2E Ch. 1.11 - Prob. 3E Ch. 1.11 - Prob. 4E Ch. 1.11 - Prob. 5E Ch. 1.11 - Prob. 6E Ch. 1.11 - Prob. 7E Ch. 1.11 - Prob. 8E Ch. 1.11 - Prob. 9E Ch. 1.11 - Prob. 10E Ch. 1.11 - Prob. 11E Ch. 1.11 - Prob. 12E Ch. 1.11 - Prob. 13E Ch. 1.11 - Prob. 14E Ch. 1.11 - Prob. 15E Ch. 1.11 - Prob. 16E Ch. 1.11 - Prob. 17E Ch. 1.11 - Prob. 18E Ch. 1.11 - Prob. 19E Ch. 1.11 - Prob. 20E Ch. 1.11 - Prob. 21E Ch. 1.11 - Prob. 22E Ch. 1.11 - Prob. 23E Ch. 1.11 - Prob. 24E Ch. 1.11 - Prob. 25E Ch. 1.11 - Prob. 26E Ch. 1.11 - Prob. 27E Ch. 1.11 - Prob. 28E Ch. 1.11 - Hookes Law Hookes Law states that the force needed...Ch. 1.11 - Prob. 30E Ch. 1.11 - Prob. 31E Ch. 1.11 - Prob. 32E Ch. 1.11 - Prob. 33E Ch. 1.11 - Prob. 34E Ch. 1.11 - Prob. 35E Ch. 1.11 - Stopping Distance The stopping distance D of a car...Ch. 1.11 - Prob. 37E Ch. 1.11 - Aerodynamic Lift The lift L on an airplane wing at...Ch. 1.11 - Drag Force on a Boat The drag force F on a boat is...Ch. 1.11 - Prob. 40E Ch. 1.11 - Prob. 41E Ch. 1.11 - Keplers Third Law Keplers Third Law of planetary...Ch. 1.11 - Radiation Energy The total radiation energy E...Ch. 1.11 - Value of a Lot The value of a building lot on...Ch. 1.11 - Prob. 45E Ch. 1.11 - Prob. 46E Ch. 1.11 - Frequency of Vibration The frequency f of...Ch. 1.11 - Spread of a Disease The rate r at which a disease...Ch. 1.11 - Prob. 49E Ch. 1 - Prob. 1RCC Ch. 1 - Prob. 2RCC Ch. 1 - Prob. 3RCC Ch. 1 - Prob. 4RCC Ch. 1 - Prob. 5RCC Ch. 1 - Prob. 6RCC Ch. 1 - Prob. 7RCC Ch. 1 - Prob. 8RCC Ch. 1 - Prob. 9RCC Ch. 1 - Prob. 10RCC Ch. 1 - Prob. 11RCC Ch. 1 - Prob. 12RCC Ch. 1 - Prob. 13RCC Ch. 1 - Prob. 14RCC Ch. 1 - Prob. 15RCC Ch. 1 - Prob. 16RCC Ch. 1 - Prob. 17RCC Ch. 1 - Prob. 18RCC Ch. 1 - Prob. 19RCC Ch. 1 - Prob. 20RCC Ch. 1 - Prob. 21RCC Ch. 1 - Prob. 22RCC Ch. 1 - Prob. 23RCC Ch. 1 - Prob. 24RCC Ch. 1 - How do you find x-intercepts and y-intercepts of a...Ch. 1 - Prob. 26RCC Ch. 1 - Prob. 27RCC Ch. 1 - Prob. 28RCC Ch. 1 - Prob. 29RCC Ch. 1 - Prob. 30RCC Ch. 1 - Prob. 31RCC Ch. 1 - Prob. 32RCC Ch. 1 - Prob. 33RCC Ch. 1 - Prob. 1RE Ch. 1 - Prob. 2RE Ch. 1 - Prob. 3RE Ch. 1 - Prob. 4RE Ch. 1 - Prob. 5RE Ch. 1 - Prob. 6RE Ch. 1 - Prob. 7RE Ch. 1 - Prob. 8RE Ch. 1 - Prob. 9RE Ch. 1 - Prob. 10RE Ch. 1 - Prob. 11RE Ch. 1 - Prob. 12RE Ch. 1 - Prob. 13RE Ch. 1 - Prob. 14RE Ch. 1 - Prob. 15RE Ch. 1 - Prob. 16RE Ch. 1 - Prob. 17RE Ch. 1 - Prob. 18RE Ch. 1 - Prob. 19RE Ch. 1 - Prob. 20RE Ch. 1 - Prob. 21RE Ch. 1 - Prob. 22RE Ch. 1 - Prob. 23RE Ch. 1 - Prob. 24RE Ch. 1 - Prob. 25RE Ch. 1 - Prob. 26RE Ch. 1 - Prob. 27RE Ch. 1 - Prob. 28RE Ch. 1 - Prob. 29RE Ch. 1 - Prob. 30RE Ch. 1 - Prob. 31RE Ch. 1 - Prob. 32RE Ch. 1 - Prob. 33RE Ch. 1 - Prob. 34RE Ch. 1 - Prob. 35RE Ch. 1 - Prob. 36RE Ch. 1 - Prob. 37RE Ch. 1 - Prob. 38RE Ch. 1 - Prob. 39RE Ch. 1 - Prob. 40RE Ch. 1 - Prob. 41RE Ch. 1 - Prob. 42RE Ch. 1 - Prob. 43RE Ch. 1 - Prob. 44RE Ch. 1 - Prob. 45RE Ch. 1 - Prob. 46RE Ch. 1 - Prob. 47RE Ch. 1 - Prob. 48RE Ch. 1 - Prob. 49RE Ch. 1 - Prob. 50RE Ch. 1 - Prob. 51RE Ch. 1 - Prob. 52RE Ch. 1 - Prob. 53RE Ch. 1 - Prob. 54RE Ch. 1 - Prob. 55RE Ch. 1 - Prob. 56RE Ch. 1 - Prob. 57RE Ch. 1 - Prob. 58RE Ch. 1 - Prob. 59RE Ch. 1 - Prob. 60RE Ch. 1 - Prob. 61RE Ch. 1 - Prob. 62RE Ch. 1 - Prob. 63RE Ch. 1 - Prob. 64RE Ch. 1 - Prob. 65RE Ch. 1 - Prob. 66RE Ch. 1 - Prob. 67RE Ch. 1 - Prob. 68RE Ch. 1 - Prob. 69RE Ch. 1 - Prob. 70RE Ch. 1 - Prob. 71RE Ch. 1 - Prob. 72RE Ch. 1 - Prob. 73RE Ch. 1 - Prob. 74RE Ch. 1 - Prob. 75RE Ch. 1 - Prob. 76RE Ch. 1 - Prob. 77RE Ch. 1 - Prob. 78RE Ch. 1 - Prob. 79RE Ch. 1 - Prob. 80RE Ch. 1 - Prob. 81RE Ch. 1 - Prob. 82RE Ch. 1 - Prob. 83RE Ch. 1 - Prob. 84RE Ch. 1 - Prob. 85RE Ch. 1 - Prob. 86RE Ch. 1 - Prob. 87RE Ch. 1 - Prob. 88RE Ch. 1 - Prob. 89RE Ch. 1 - Prob. 90RE Ch. 1 - Prob. 91RE Ch. 1 - Prob. 92RE Ch. 1 - Prob. 93RE Ch. 1 - Prob. 94RE Ch. 1 - Prob. 95RE Ch. 1 - Prob. 96RE Ch. 1 - Prob. 97RE Ch. 1 - Prob. 98RE Ch. 1 - Prob. 99RE Ch. 1 - Prob. 100RE Ch. 1 - Prob. 101RE Ch. 1 - Prob. 102RE Ch. 1 - Prob. 103RE Ch. 1 - Prob. 104RE Ch. 1 - Prob. 105RE Ch. 1 - Prob. 106RE Ch. 1 - Prob. 107RE Ch. 1 - Prob. 108RE Ch. 1 - Prob. 109RE Ch. 1 - Prob. 110RE Ch. 1 - Prob. 111RE Ch. 1 - Prob. 112RE Ch. 1 - Prob. 113RE Ch. 1 - Prob. 114RE Ch. 1 - Prob. 115RE Ch. 1 - Prob. 116RE Ch. 1 - Prob. 117RE Ch. 1 - Prob. 118RE Ch. 1 - Prob. 119RE Ch. 1 - Prob. 120RE Ch. 1 - Prob. 121RE Ch. 1 - Prob. 122RE Ch. 1 - Prob. 123RE Ch. 1 - Prob. 124RE Ch. 1 - Prob. 125RE Ch. 1 - Prob. 126RE Ch. 1 - Prob. 127RE Ch. 1 - Prob. 128RE Ch. 1 - Prob. 129RE Ch. 1 - Prob. 130RE Ch. 1 - Prob. 131RE Ch. 1 - Prob. 132RE Ch. 1 - Prob. 133RE Ch. 1 - Prob. 134RE Ch. 1 - Prob. 135RE Ch. 1 - Prob. 136RE Ch. 1 - Prob. 137RE Ch. 1 - Prob. 138RE Ch. 1 - (a) Graph the intervals (5, 3] and (2, ) on the...Ch. 1 - Prob. 2T Ch. 1 - Write each number in scientific notation. (a)...Ch. 1 - Simplify each expression. Write your final answer...Ch. 1 - Prob. 5T Ch. 1 - Prob. 6T Ch. 1 - Prob. 7T Ch. 1 - Prob. 8T Ch. 1 - Mary drove from Amity to Belleville at a speed of...Ch. 1 - Prob. 10T Ch. 1 - Prob. 11T Ch. 1 - A bottle of medicine is to be stored at a...Ch. 1 - Prob. 13T Ch. 1 - Prob. 14T Ch. 1 - (a) Plot the points P(0, 3), Q(3, 0), and R(6, 3)...Ch. 1 - Prob. 16T Ch. 1 - Prob. 17T Ch. 1 - Prob. 18T Ch. 1 - Write the linear equation 2x 3y = 15 in...Ch. 1 - Prob. 20T Ch. 1 - A geologist measures the temperature T (in C) of...Ch. 1 - The maximum weight M that can be supported by a...Ch. 1 - Femur Length and Height Anthropologists use a...Ch. 1 - Demand for Soft Drinks A convenience store manager...Ch. 1 - Prob. 3P Ch. 1 - Prob. 4P Ch. 1 - Prob. 5P Ch. 1 - Prob. 6P Ch. 1 - Prob. 7P Ch. 1 - Noise and Intelligibility Audiologists study the...Ch. 1 - Life Expectancy The average life expectancy in the...Ch. 1 - Prob. 10P Ch. 1 - Prob. 11P Ch. 1 - Prob. 12P Ch. 1 - Prob. 13P

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.