Chapter 1.8, Problem 69E

To determine

To calculate: The x- and y- intercepts for the equation $y=\sqrt{4-x^2}$ and test the symmetry of the equation. Also construct the table to sketch the graph of the equation.

Answer to Problem 69E

The x-intercepts are $\pm 2$ and y-intercept is $2$ . The equation is symmetric about y-axis.Graph of the equation $y=\sqrt{4-x^2}$ is provided below,

  

Explanation of Solution

Given information:

The equation $y=\sqrt{4-x^2}$ .

Formula used:

The function is symmetric about the x-axis, when y is replaced by $-y$ , the equation remains unchanged.

The function is symmetric about the y-axis, when x is replaced by $-x$ , the equation remains unchanged.

The function is symmetric with respect to origin, when y is replaced by $-y$ and x is replaced by $-x$ , the equation remains unchanged.

The x-intercepts are the points on x-axis where the graph of the equation intersects the x-axis.

The y-intercepts are the points on y-axis where the graph of the equation intersects the y-axis.

Calculation:

It is provided that the equation is $y=\sqrt{4-x^2}$ . Construct a table to evaluate the value of y for different values of x.

Substitute the point $x=-2$ in the equation $y=\sqrt{4-x^2}$ ,

  $\begin{array}{c}y=\sqrt{4-{\left(-2\right)}^2}\\ y=\sqrt{4-4}\\ y=0\end{array}$

Substitute the point $x=0$ in the equation $y=\sqrt{4-x^2}$ ,

  $\begin{array}{c}y=\sqrt{4-0^2}\\ y=\sqrt{4}\\ y=2\end{array}$

Substitute the point $x=1$ in the equation $y=\sqrt{4-x^2}$ ,

  $\begin{array}{c}y=\sqrt{4-{\left(1\right)}^2}\\ y=\sqrt{4-1}\\ y=\sqrt{3}\end{array}$

Substitute the point $x=2$ in the equation $y=\sqrt{4-x^2}$ ,

  $\begin{array}{c}y=\sqrt{4-{\left(2\right)}^2}\\ y=\sqrt{4-4}\\ y=0\end{array}$

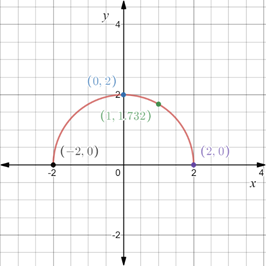
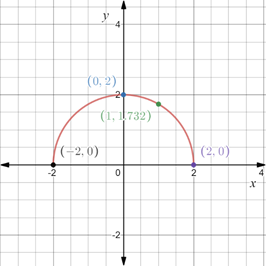
Construct a table with the values obtained above,

  $\begin{array}{ccc}x& y& \left(x,y\right)\\ -2& 0& \left(-2,0\right)\\ 0& 2& \left(0,2\right)\\ 1& \sqrt{3}& \left(1,\sqrt{3}\right)\\ 2& 0& \left(2,0\right)\end{array}$

In the coordinate plane plot the points obtained above and connect them through a line.

The graph of the equation is provided below $y=\sqrt{4-x^2}$ .

  

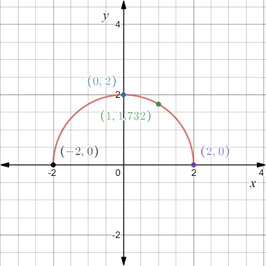
Recall that the x-intercepts are the points on x-axis where the graph of the equation intersects the x-axis.

Substitute $y=0$ in the equation $y=\sqrt{4-x^2}$ ,

  $\begin{array}{c}0=\sqrt{4-x^2}\\ 4-x^2=0\\ x^2=4\\ x=\pm 2\end{array}$

Therefore, x-intercepts are $\pm 2$ .

Recall that the y-intercepts are the points on x-axis where the graph of the equation intersects the y-axis.

Substitute $x=0$ in the equation $y=\sqrt{4-x^2}$ ,

  $\begin{array}{c}y=\sqrt{4-0^2}\\ y=\sqrt{4}\\ y=2\end{array}$

Therefore, y-intercept is $2$ .

Recall that the function is symmetric about the x-axis, when y is replaced by $-y$ , the equation remains unchanged.

Replace y by $-y$ in the equation $y=\sqrt{4-x^2}$ ,

  $-y=\sqrt{4-x^2}$

The equation is changed. Therefore, the equation $y=\sqrt{4-x^2}$ is not symmetricabout the x-axis.

Recall that the function is symmetric about the y-axis, when x is replaced by $-x$ , the equation remains unchanged.

Replace x by $-x$ in the equation $y=\sqrt{4-x^2}$ ,

  $\begin{array}{c}y=\sqrt{4-{\left(-x\right)}^2}\\ y=\sqrt{4-x^2}\end{array}$

The equation is unchanged. Therefore, the equation $y=\sqrt{4-x^2}$ is symmetricabout the y-axis.

Recall that the function is symmetric with respect to origin, when y is replaced by $-y$ and x is replaced by $-x$ , the equation remains unchanged.

Replace x by $-x$ and y by $-y$ in the equation $y=\sqrt{4-x^2}$ ,

  $\begin{array}{c}-y=\sqrt{4-{\left(-x\right)}^2}\\ -y=\sqrt{4-x^2}\end{array}$

The equation is changed. Therefore, the equation $y=\sqrt{4-x^2}$ is not symmetricabout the origin.

Thus, the x-intercepts are $\pm 2$ and y-intercept is $2$ . The equation is symmetric about y-axis.Graph of the equation $y=\sqrt{4-x^2}$ is provided below,