Chapter 9.12, Problem 142P

To determine

The exergy destruction associated with each of the processes of the Brayton cycle.

Answer to Problem 142P

The exergy destruction associated with process 1-2 of the given Brayton cycle is $28.08\text{kJ}/\text{kg}$.

The exergy destruction associated with process 2-3 of the given Brayton cycle is $100.3\text{kJ}/\text{kg}$.

The exergy destruction associated with process 3-4 of the given Brayton cycle is $32.86\text{kJ}/\text{kg}$.

The exergy destruction associated with process 4-1 of the given Brayton cycle is $197.93\text{kJ}/\text{kg}$.

Explanation of Solution

Show the simple Brayton cycle, and with air as the working fluid on $T-s$ diagram.

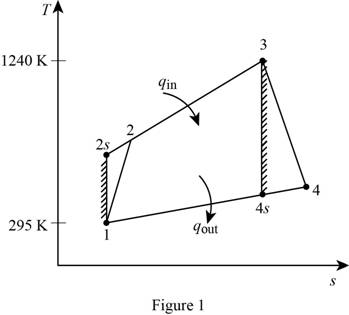
For the given simple Brayton cycle with air as the working fluid, let $T_i$, $P_i$, $h_i$ and $P_{r_i}$ be the temperature, pressure, specific enthalpy and relative pressure at $i^{th}$ state respectively.

Write the expression of pressure ratio relation for the process 1-2.

$P_{r_2}=\frac{P_2}{P_1}{P}_{r_1}$ (I)

Write the relation of pressure ratio and pressure for the process 3-4.

$P_{r_4}=\frac{P_4}{P_3}{P}_{r_3}$ (II)

Write the expression of efficiency of the compressor $\left({\eta }_C\right)$.

${\eta }_C=\frac{h_{2s}-h_1}{h_2-h_1}$ (III)

Write the expression of efficiency of the turbine $\left({\eta }_T\right)$.

${\eta }_T=\frac{h_3-h_4}{h_3-h_{4s}}$ (IV)

Write the expression of heat input to the Brayton cycle $\left(q_{\text{in}}\right)$.

$q_{\text{in}}=\left(h_3-h_2\right)$ (V)

Write the expression of heat rejected by the Brayton cycle $\left(q_{\text{out}}\right)$.

$q_{\text{out}}=\left(h_4-h_1\right)$ (VI)

Write the expression of exergy destruction associated with the process 1-2 of the given Brayton cycle $\left(x_{\text{destroyed,12}}\right)$.

$x_{\text{destroyed,12}}=T_0\left(s_2-s_1\right)$

$x_{\text{destroyed,12}}=T_0\left(s_2^{\circ }-s_1^{\circ }-R\ln \frac{P_2}{P_1}\right)$ (VII)

Here, temperature of the surroundings is $T_0$, gas constant of air is R, entropy of air at state 2 as a function of temperature alone is $s_2^{\circ }$, and entropy of air at state 1 as a function of temperature alone is $s_1^{\circ }$.

Write the expression of exergy destruction associated with the process 2-3 of the given Brayton cycle $\left(x_{\text{destroyed,23}}\right)$.

$x_{\text{destroyed,23}}=T_0\left(s_3-s_2+\frac{-q_{\text{in}}}{T_H}\right)$

$x_{\text{destroyed,23}}=T_0\left(s_3^{\circ }-s_2^{\circ }-R\ln \frac{P_3}{P_2}+\frac{-q_{\text{in}}}{T_H}\right)$ (VIII)

Here, temperature of the heat source is $T_H$, entropy of air at state 2 as a function of temperature alone is $s_2^{\circ }$, and entropy of air at state 3 as a function of temperature alone is $s_3^{\circ }$.

Write the expression of exergy destruction associated with the process 3-4 of the given Brayton cycle $\left(x_{\text{destroyed,34}}\right)$.

$x_{\text{destroyed,34}}=T_0\left(s_4-s_3\right)$

$x_{\text{destroyed,34}}=T_0\left(s_4^{\circ }-s_3^{\circ }-R\ln \frac{P_4}{P_3}\right)$ (IX)

Here, entropy of air at state 3 as a function of temperature is $s_3^{\circ }$, and entropy of air at state 4 as a function of temperature is $s_4^{\circ }$.

Write the expression of exergy destruction associated with the process 4-1 of the given Brayton cycle $\left(x_{\text{destroyed,41}}\right)$.

$x_{\text{destroyed,41}}=T_0\left(s_1-s_4+\frac{q_{\text{out}}}{T_L}\right)$

$x_{\text{destroyed,41}}=T_0\left(s_1^{\circ }-s_4^{\circ }-R\ln \frac{P_1}{P_4}+\frac{q_{\text{out}}}{T_L}\right)$ (X)

Here, temperature of the sink is $T_L$, entropy of air at state 1 as a function of temperature alone is $s_1^{\circ }$, and entropy of air at state 4 as a function of temperature alone is $s_4^{\circ }$.

Conclusion:

Refer Table A-17E given in the textbook to find the properties of air at 295 K $\left(T_1\right)$, which gives $295.17\text{kJ}/\text{kg}$ for $h_1$, 1.3068 for $P_{r_1}$ and $1.68515\text{kJ}/\text{kg}\cdot \text{K}$ for $s_1^{\circ }$.

Substitute 10 for $\frac{P_2}{P_1}$, and 1.3068 for $P_{r_1}$ in Equation (I).

$\begin{array}{c}{P}_{r_2}=\left(10\right)\left(1.3068\right)\\ =13.07\end{array}$

Refer Table A-17E given in the textbook to find the properties of air at 13.07 $\left(P_{r_1}\right)$, which gives $570.26\text{kJ}/\text{kg}$ for $h_{2s}$, and 564.9 K for $T_{2s}$.

Refer Table A-17E given in the textbook to find the properties of air at 1,240 K $\left(T_3\right)$, which gives $1,324.93\text{kJ}/\text{kg}$ for $h_3$, 272.3 for $P_{r_3}$ and $3.21751\text{kJ}/\text{kg}\cdot \text{K}$ for $s_3^{\circ }$.

Substitute $\frac{1}{10}$ for $\frac{P_4}{P_3}$, and 272.3 for $P_{r_3}$ in Equation (II).

$\begin{array}{c}{P}_{r_4}=\left(\frac{1}{10}\right)\left(272.3\right)\\ =27.23\end{array}$

Refer Table A-17 given in the textbook to find the properties of air at 27.23 $\left(P_{r_4}\right)$, which gives $702.07\text{kJ}/\text{kg}$ for $h_{4s}$, and 689.6 K for $T_{4s}$.

Rearrange Equation (III) and substitute $295.17\text{kJ}/\text{kg}$ for $h_1$, $570.26\text{kJ}/\text{kg}$ for $h_{2s}$, and 0.83 for ${\eta }_C$.

$\begin{array}{c}{h}_2=h_1+\frac{h_{2s}-h_1}{{\eta }_C}\\ =295.17\text{kJ}/\text{kg}+\frac{\left(570.26-295.17\right)\text{kJ}/\text{kg}}{0.83}\\ =626.60\text{kJ}/\text{kg}\end{array}$

Refer Table A-17E given in the textbook to find the properties of air at $626.60\text{kJ}/\text{kg}$ $\left(h_2\right)$, which gives $2.44117\text{kJ}/\text{kg}\cdot \text{K}$ for $s_2^{\circ }$.

Rearrange Equation (IV) and substitute $1,324.93\text{kJ}/\text{kg}$ for $h_3$, $702.07\text{kJ}/\text{kg}$ for $h_{4s}$, and 0.87 for ${\eta }_T$.

$\begin{array}{c}{h}_4=h_3-{\eta }_T\left(h_3-h_{4s}\right)\\ =1,324.93\text{kJ}/\text{kg}+\left(0.87\right)\left(1,324.93-702.07\right)\text{kJ}/\text{kg}\\ =783.04\text{}\text{kJ}/\text{kg}\end{array}$

Refer Table A-17 given in the textbook, to find the properties of air at $783.04\text{}\text{kJ}/\text{kg}$ $\left(h_4\right)$, which gives 764.4 K for $T_4$ and $2.66807\text{kJ}/\text{kg}\cdot \text{K}$ for $s_4^{\circ }$.

Substitute $1,324.93\text{kJ}/\text{kg}$ for $h_3$, and $626.60\text{kJ}/\text{kg}$ for $h_2$ in Equation (V).

$\begin{array}{c}{q}_{\text{in}}=\left(1,324.93-626.60\right)\text{kJ}/\text{kg}\\ =698.3\text{kJ}/\text{kg}\end{array}$

Substitute $783.04\text{kJ}/\text{kg}$ for $h_4$, and $295.17\text{kJ}/\text{kg}$ for $h_1$ in Equation (VI).

$\begin{array}{c}{q}_{\text{out}}=\left(783.04-295.17\right)\text{kJ}/\text{kg}\\ =487.9\text{kJ}/\text{kg}\end{array}$

Substitute 295 K for $T_0$, $1.68515\text{kJ}/\text{kg}\cdot \text{K}$ for $s_1^{\circ }$, $2.44117\text{kJ}/\text{kg}\cdot \text{K}$ for $s_2^{\circ }$, $0.287\text{kJ}/\text{kg}\cdot \text{K}$ for R, and 10 for $\frac{P_2}{P_1}$ in Equation (VII).

$\begin{array}{c}{x}_{\text{destroyed,12}}=\left(295\text{K}\right)\left[\left(2.44117-1.68515\right)\text{kJ}/\text{kg}\cdot \text{K}-\left(0.287\text{kJ}/\text{kg}\cdot \text{K}\right)\ln \left(10\right)\right]\\ =28.08\text{kJ}/\text{kg}\end{array}$

Thus, the exergy destruction associated with process 1-2 of the given Brayton cycle is $28.08\text{kJ}/\text{kg}$.

Substitute 295 K for $T_0$, $3.21751\text{kJ}/\text{kg}\cdot \text{K}$ for $s_3^{\circ }$, $2.44117\text{kJ}/\text{kg}\cdot \text{K}$ for $s_2^{\circ }$, $0.287\text{kJ}/\text{kg}\cdot \text{K}$ for R, 1,600 K for $T_H$, and $698.3\text{kJ}/\text{kg}$ for $q_{\text{in}}$ in Equation (VIII). For the process 2-3, pressure remains constant, hence substitute 0 for $\ln \frac{P_3}{P_2}$.

$\begin{array}{c}{x}_{\text{destroyed,23}}=\left(295\text{K}\right)\left[\begin{array}{l}\left(3.21751-2.44117\right)\text{kJ}/\text{kg}\cdot \text{K}\\ -\left(0.287\text{kJ}/\text{kg}\cdot \text{K}\right)\left(0\right)-\frac{698.3\text{kJ}/\text{kg}}{1,600\text{K}}\end{array}\right]\\ =100.3\text{kJ}/\text{kg}\end{array}$

Thus, the exergy destruction associated with process 2-3 of the given Brayton cycle is $100.3\text{kJ}/\text{kg}$.

Substitute 295 K for $T_0$, $3.21751\text{kJ}/\text{kg}\cdot \text{K}$ for $s_3^{\circ }$, $2.66807\text{kJ}/\text{kg}\cdot \text{K}$ for $s_4^{\circ }$, $0.287\text{kJ}/\text{kg}\cdot \text{K}$ for R, and $\frac{1}{10}$ for $\frac{P_4}{P_3}$ in Equation (IX).

$\begin{array}{c}{x}_{\text{destroyed,34}}=\left(295\text{K}\right)\left[\left(2.66807-3.21751\right)\text{kJ}/\text{kg}\cdot \text{K}-\left(0.287\text{kJ}/\text{kg}\cdot \text{K}\right)\ln \left(\frac{1}{10}\right)\right]\\ =32.86\text{kJ}/\text{kg}\end{array}$

Thus, the exergy destruction associated with process 3-4 of the given Brayton cycle is $32.86\text{kJ}/\text{kg}$.

Substitute 295 K for $T_0$, $1.68515\text{kJ}/\text{kg}\cdot \text{K}$ for $s_1^{\circ }$, $2.66807\text{kJ}/\text{kg}\cdot \text{K}$ for $s_4^{\circ }$, $0.287\text{kJ}/\text{kg}\cdot \text{K}$ for R, 295 K for $T_L$, and $487.9\text{kJ}/\text{kg}$ for $q_{\text{out}}$ in Equation (X). For the process 4-1, pressure remains constant, hence substitute 0 for $\ln \frac{P_1}{P_4}$.

$\begin{array}{c}{x}_{\text{destroyed,41}}=\left(295\text{K}\right)\left[\begin{array}{l}\left(1.68515-2.66807\right)\text{kJ}/\text{kg}\cdot \text{K}\\ -\left(0.287\text{kJ}/\text{kg}\cdot \text{K}\right)\left(0\right)+\frac{487.9\text{kJ}/\text{kg}}{295\text{K}}\end{array}\right]\\ =197.93\text{kJ}/\text{kg}\end{array}$

Thus, the exergy destruction associated with process 4-1 of the given Brayton cycle is $197.93\text{kJ}/\text{kg}$.