Chapter 9, Problem 9.72P

All parameters associated with the instrumentation amplifier in Figure 9.26are the same as given in Exercise Ex 9.8, except that resistor $R_3$ , which isconnected to the inverting terminal of A3, is $R_3=30k\Omega \pm 5\%$ . Determinethe maximum common-mode gain.

To determine

The value of maximum common mode gain.

Answer to Problem 9.72P

The maximum value of the voltage gain is $0.0395$ .

Explanation of Solution

Calculation:

The given diagram is shown in Figure 1

  

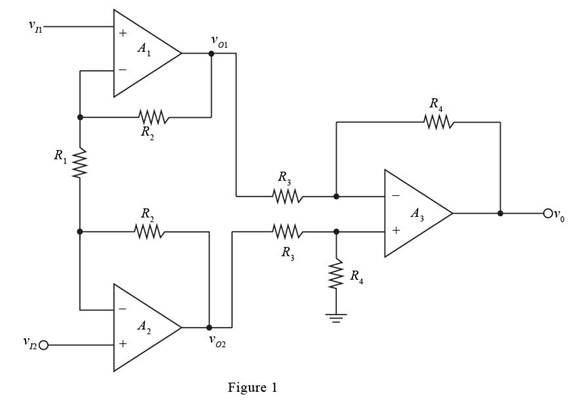
Mark the voltages and current and redraw the circuit.

The required diagram is shown in Figure 2

  

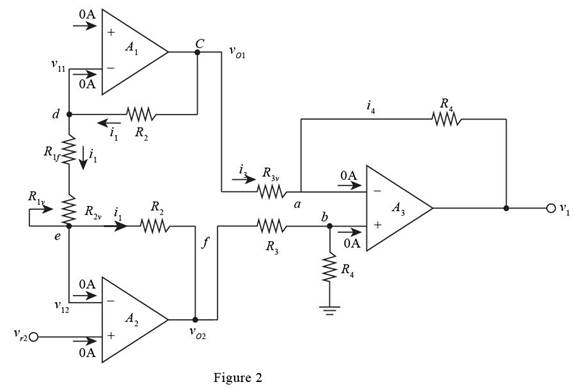
The expression for the voltage $v_b$ by voltage division rule is given by,

  $v_b=\frac{R_4{v}_{O2}}{R_3+R_4}$

The expression for the current at the node $v_a$ is given by,

  $v_a=v_b$

Substitute $\frac{R_4{v}_{O2}}{R_3+R_4}$ for $v_b$ in the above equation.

  $v_a=\frac{R_4{v}_{O2}}{R_3+R_4}$

Apply KCL at the node $v_a$ .

  $\begin{array}{l}\frac{v_{O1}-v_a}{R_{3x}}=\frac{v_a-v_O}{R_4}\\ v_O=\left(-\frac{R_4}{R_{3x}}\right)v_{O1}+\left(1+\frac{R_4}{R_{3x}}\right)v_a\end{array}$

Substitute $\frac{R_4{v}_{O2}}{R_3+R_4}$ for $v_a$ in the above equation.

  $v_O=\left(-\frac{R_4}{R_{3x}}\right)v_{O1}+\left(1+\frac{R_4}{R_{3x}}\right)\frac{R_4{v}_{O2}}{R_3+R_4}$ ........ (1)

The expression for the value of the current $i_1$ is given by,

  $i_1=\frac{v_{I1}-v_{I2}}{R_1}$

The expression for the voltage $v_{O1}$ is given by,

  $v_{O1}-v_{I1}=i_1{R}_2$

Substitute $\frac{v_{I1}-v_{I2}}{R_1}$ for $i_1$ in the above equation.

  $v_{O1}=v_{I1}+\left(\frac{v_{I1}-v_{I2}}{R_1}\right)R_2$

The expression for the voltage $v_{O2}$ is given by,

  $v_{O2}=v_{I2}-i_1{R}_2$

Substitute $\frac{v_{I1}-v_{I2}}{R_1}$ for $i_1$ in the above equation.

  $v_{O2}=v_{I2}-\left(\frac{v_{I1}-v_{I2}}{R_1}\right)R_2$

Substitute $v_{I1}+\left(\frac{v_{I1}-v_{I2}}{R_1}\right)R_2$ for $v_{O1}$ and $v_{I2}-\left(\frac{v_{I1}-v_{I2}}{R_1}\right)R_2$ for $v_{O2}$ in equation (1)

  $\begin{array}{c}{v}_O=\left(-\frac{R_4}{R_{3x}}\right)\left(v_{I1}+\left(\frac{v_{I1}-v_{I2}}{R_1}\right)R_2\right)+\left(1+\frac{R_4}{R_{3x}}\right)\frac{R_4}{R_3+R_4}\left(v_{I2}-\left(\frac{v_{I1}-v_{I2}}{R_1}\right)R_2\right)\\ =\left(\frac{v_{I1}-v_{I2}}{R_1}\right)R_2\left[\left(\frac{-R_4}{R_{3x}}\right)-\left(1+\frac{R_4}{R_{3x}}\right)\left(1+\frac{R_4}{R_3+R_4}\right)\right]-v_{I1}\left(\frac{R_4}{R_{3x}}\right)+v_{I2}\left(1+\frac{R_4}{R_{3x}}\right)\left(\frac{R_4}{R_3+R_4}\right)\end{array}$ ........ (2)

The expression for the common mode voltage is given by,

  $v_{cm}=\frac{v_{I1}+v_{I2}}{2}$

The expression for the differential voltage is given by,

  $v_d=v_{I2}-v_{I1}$

The expression for the voltage $v_{I2}$ is given by,

  $v_{I2}=v_{cm}+\frac{v_d}{2}$

The expression for the voltage $v_{I1}$ is given by,

  $v_{I1}=v_{cm}-\frac{v_d}{2}$

Substitute $v_d$ for $v_{I2}-v_{I1}$ , $v_{cm}+\frac{v_d}{2}$ for $v_{I2}$ and $v_{cm}-\frac{v_d}{2}$ for $v_{I1}$ in equation (2).

  $\begin{array}{c}{v}_O=\left[\begin{array}{l}\left(\frac{v_d}{R_1}\right)R_2\left[\left(\frac{-R_4}{R_{3x}}\right)-\left(1+\frac{R_4}{R_{3x}}\right)\left(1+\frac{R_4}{R_3+R_4}\right)\right]-\left(v_{cm}-\frac{v_d}{2}\right)\left(\frac{R_4}{R_{3x}}\right)\\ +\left(v_{cm}+\frac{v_d}{2}\right)\left(1+\frac{R_4}{R_{3x}}\right)\left(\frac{R_4}{R_3+R_4}\right)\end{array}\right]\\ =\left[\begin{array}{l}{v}_d\left[\left(\frac{R_2}{R_1}+\frac{1}{2}\right)\left(\frac{R_4}{R_{3x}}\right)\left(\frac{R_2}{R_1}+\frac{1}{2}\right)\left(1+\frac{R_4}{R_{3x}}\right)\left(\frac{R_4}{R_3+R_4}\right)\right]\\ +v_{cm}\left[\left(-\frac{R_4}{R_{3x}}\right)+\left(1+\frac{R_4}{R_{3x}}\right)\left(\frac{R_4}{R_3+R_4}\right)\right]\end{array}\right]\end{array}$ ........ (3)

The general expression for the output equation is given by,

  $v_O=A_{cm}{v}_{cm}+A_d{v}_d$

From above and from equation (3), the expression for the common mode gain is evaluated as,

  $A_{cm}=\left(-\frac{R_4}{R_{3x}}\right)+\left(1+\frac{R_4}{R_{3x}}\right)\left(\frac{R_4}{R_3+R_4}\right)$

Substitute $90\text{k}\Omega$ for $R_4$ , $30\text{k}\Omega$ for $R_3$ and $30\text{k}\Omega \pm 5\%$ for $R_{3x}$ in the above equation.

  $\begin{array}{c}{A}_{cm}=\left(-\frac{90\text{k}\Omega }{30\text{k}\Omega \pm 5\%}\right)+\left(1+\frac{90\text{k}\Omega }{30\text{k}\Omega \pm 5\%}\right)\left(\frac{90\text{k}\Omega }{30\text{k}\Omega +90\text{k}\Omega }\right)\\ =\frac{1}{4}\left[3-\left(\frac{90}{30\pm 5\%}\right)\right]\end{array}$

From above the range of the common mode voltage gain is given by,

  $\begin{array}{l}\frac{1}{4}\left[3-\left(\frac{90}{30-5\%}\right)\right]\le A_{cm}\le \frac{1}{4}\left[3-\left(\frac{90}{30+5\%}\right)\right]\\ -0.0395\le A_{cm}\le 0.0357\end{array}$

The maximum value of the voltage gain is given by,

  ${\left|A_{cm}\right|}_{\max }=0.0395$

Conclusion:

Therefore, themaximum value of the voltage gain is $0.0395$ .