Chapter 7.1, Problem 11E

(a)

To determine

To graph: The population distribution given that there are 3000 students in this school.

Explanation of Solution

Given information:

Percent of students who did their assigned homework last week = 60%

Number of students for SRS = 100

The dotplot:

  

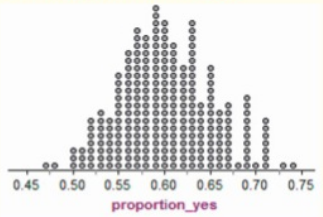
Given that the number of students in the school is 3000 and the percent of students who did all their homework last week is 60%.

So, the number of students who did their homework last week is,

  $\begin{array}{c}60\%\times 3000=\frac{60}{1\cancel{00}}\times 30\cancel{00}\\ =60\times 30\\ =1800\end{array}$

To find the number of students who did not do their homework last week, subtract 1800 from 3000.

  $3000-1800=1200$

The required graph of the population distribution is shown below:

  

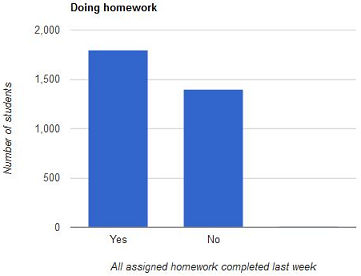
In the above graph, the widths of the bars are equal and the heights of the bars are shown according to the number of students.

(b)

To determine

To graph: The distribution of sample data for the SRS of size 100 taken by the AP Statistics students.

Explanation of Solution

Given information:

Percent of students who did their assigned homework last week = 60%

Number of students for SRS = 100

The dotplot:

  

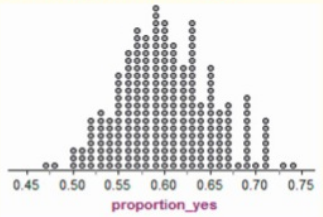
Given that the number of students in the sample is 100.

Percent of students of who did their homework last week is 60%.

Thus the number of students who did their homework from the sample of 100 students is,

  $\begin{array}{c}60\%\times 100=\frac{60}{\cancel{100}}\times \cancel{100}\\ =60\end{array}$

To find the number of students who did not their homework last week from the sample of 100 students, subtract 60 from 100.

  $100-60=40$

The required graph of the population distribution is shown below:

  

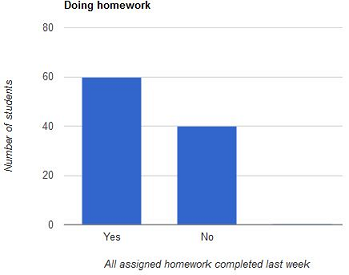
In the above graph, the widths of the bars are equal and the heights of the bars are shown according to the number of students.