Concept explainers
Videos
Advertising Spend by Companies. Advertising Age annually compiles a list of the 100 companies that spend the most on advertising. Consumer-goods company Procter & Gamble has often topped the list, spending billions of dollars annually. Consider the data found in the file Advertising. It contains annual advertising expenditures for a sample of 20 companies in the automotive sector and 20 companies in the department store sector.
- a. What is the
mean advertising spent for each sector? - b. What is the standard deviation for each sector?
- c. What is the
range of advertising spent for each sector? - d. What is the
interquartile range for each sector? - e. Based on this sample and your answers to parts (a) to (d), comment on any differences in the advertising spending in the automotive companies versus the department store companies.
a.
Find the mean advertising spent for each sector.
Answer to Problem 32E
The mean annual advertising expenditure in the automotive sector is 1,960.1.
The mean annual advertising expenditure in the Department Store sector is 692.85.
Explanation of Solution
Calculation:
The data represent the annual advertising expenditures for a sample of 20 companies in the automotive sector and another sample of 20 companies in the department store sector.
Automotive sector:
Software procedure:
Step by step procedure to obtain the descriptive statistics using EXCEL is as follows:
- In an EXCEL sheet enter the values of first sample and label it as Automotive.
- Go to Data > Data Analysis (in case it is not default, take the Analysis ToolPak from Excel Add Ins) > Descriptive statistics.
- Enter Input Range as $A$2:$A$21, select Columns in Grouped By, tick on Summary statistics.
- Click on OK.
Output using EXCEL is given as follows:
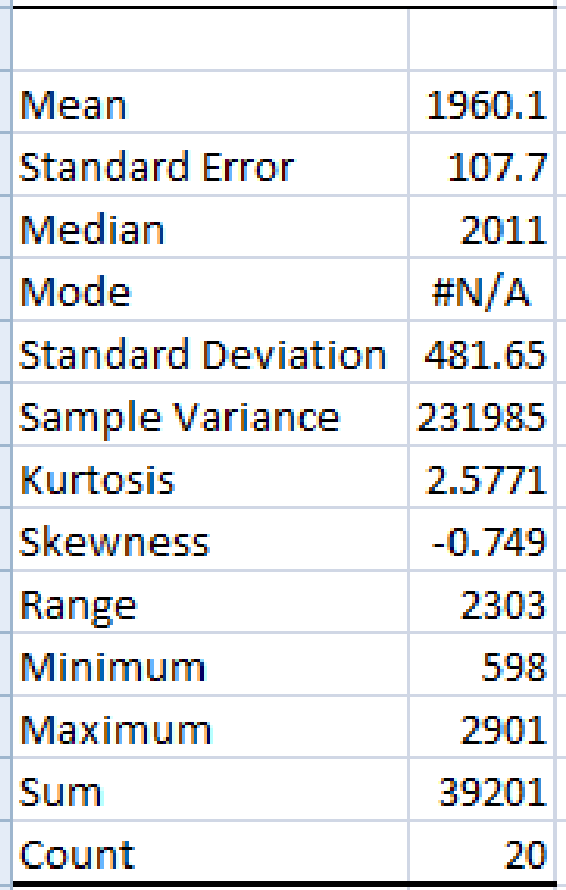
From the EXCEL output, mean is 1,960.1.
Thus, the mean annual advertising expenditure in the automotive sector is 1,960.1.
Department store sector:
Software procedure:
Step by step procedure to obtain the descriptive statistics using EXCEL is as follows:
- In an EXCEL sheet enter the values of second sample and label it as Department store.
- Go to Data > Data Analysis (in case it is not default, take the Analysis ToolPak from Excel Add Ins) > Descriptive statistics.
- Enter Input Range as $B$2:$B$21, select Columns in Grouped By, tick on Summary statistics.
- Click on OK.
Output using EXCEL is given as follows:
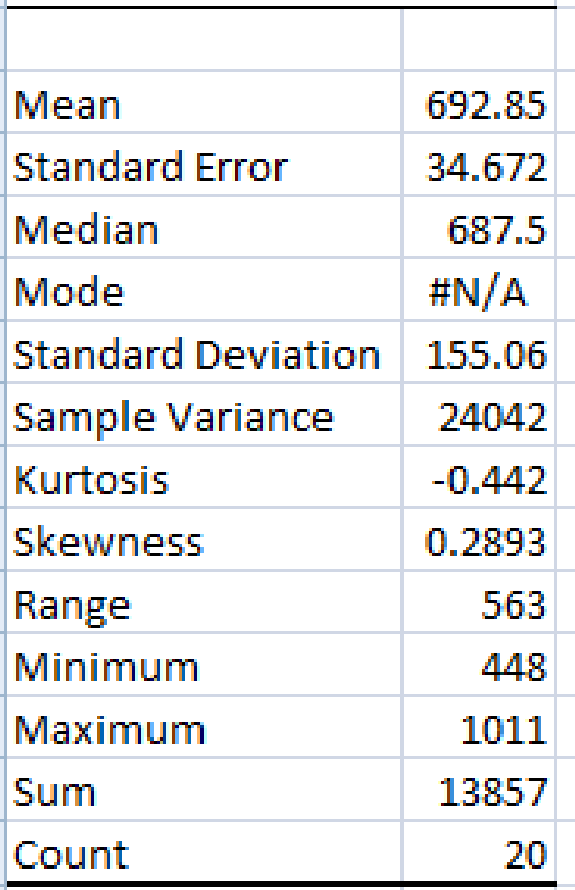
From the EXCEL output, mean is 692.85.
Thus, the mean annual advertising expenditure in the automotive sector is 692.85.
b.
Find the standard deviation for each sector.
Answer to Problem 32E
The standard deviation for annual advertising expenditure in the automotive sector is 481.65.
The standard deviation for annual advertising expenditure in the Department Store is 155.06.
Explanation of Solution
Calculation:
From the EXCEL output obtained in Part (a), the standard deviation for annual advertising expenditure in the automotive sector is 481.65 and the standard deviation for annual advertising expenditure in the Department Store is 155.06.
Thus, the standard deviations for annual advertising expenditure in the automotive sector, and Department store are 481.65, and 155.06, respectively.
c.
Find the range of advertising spent for each sector.
Answer to Problem 32E
The range of annual advertising expenditure in the automotive sector is 2,303.
The range of annual advertising expenditure in the Department Store is 563.
Explanation of Solution
Calculation:
From the EXCEL output obtained in Part (a), the range of annual advertising expenditure in the automotive sector is 2,303 and the range of annual advertising expenditure in the Department Store is 563.
Thus, the range of annual advertising expenditure in the automotive sector, and Department store are 2,303, and 563, respectively.
d.
Find the interquartile range for each sector.
Answer to Problem 32E
The inter quartile range for automotive sector is 525.5.
The inter quartile range for Department Store is 222.5.
Explanation of Solution
Automobile:
The first and third quartiles are obtained for the annual advertising expenditures in the automotive sector.
First quartile:
The EXCEL function to compute first quartile is
Software Procedure:
Step by step procedure to obtain the first quartile using EXCEL is as follows:
- In an EXCEL sheet enter the values of first sample and label it as Automotive.
- In a cell enter the formula QUARTILE.EXC ($A$2:$A$21,1).
- Click on OK.
Output using EXCEL is given as follows:
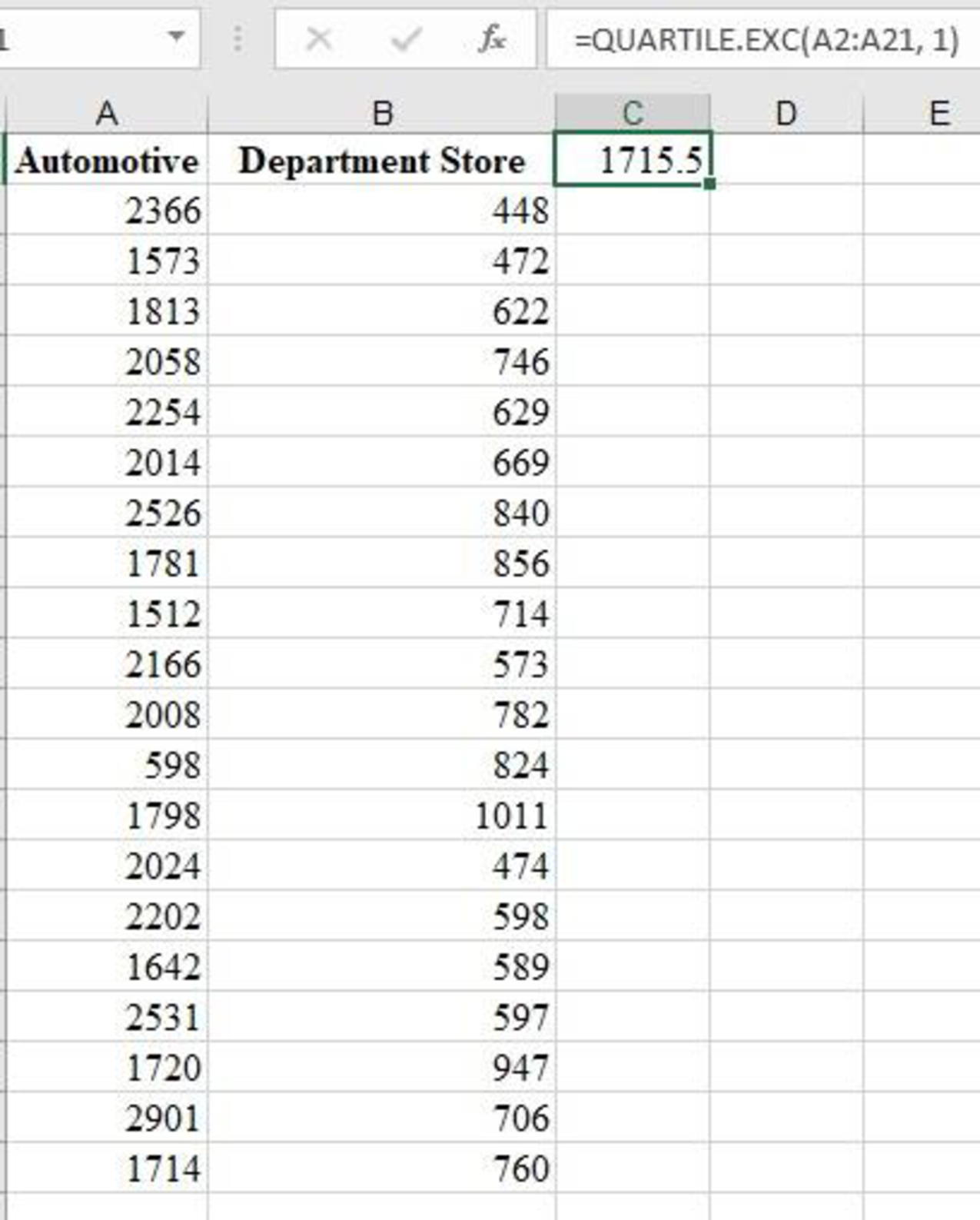
From the EXCEL output, the first quartile of the sample data is 1,715.5.
Third quartile:
The EXCEL function to compute third quartile is
Software Procedure:
Step by step procedure to obtain the third quartile using EXCEL is as follows:
- In an EXCEL sheet enter the values of first sample and label it as Automotive.
- In a cell enter the formula QUARTILE.EXC ($A$2:$A$21,3).
- Click on OK.
Output using EXCEL is given as follows:
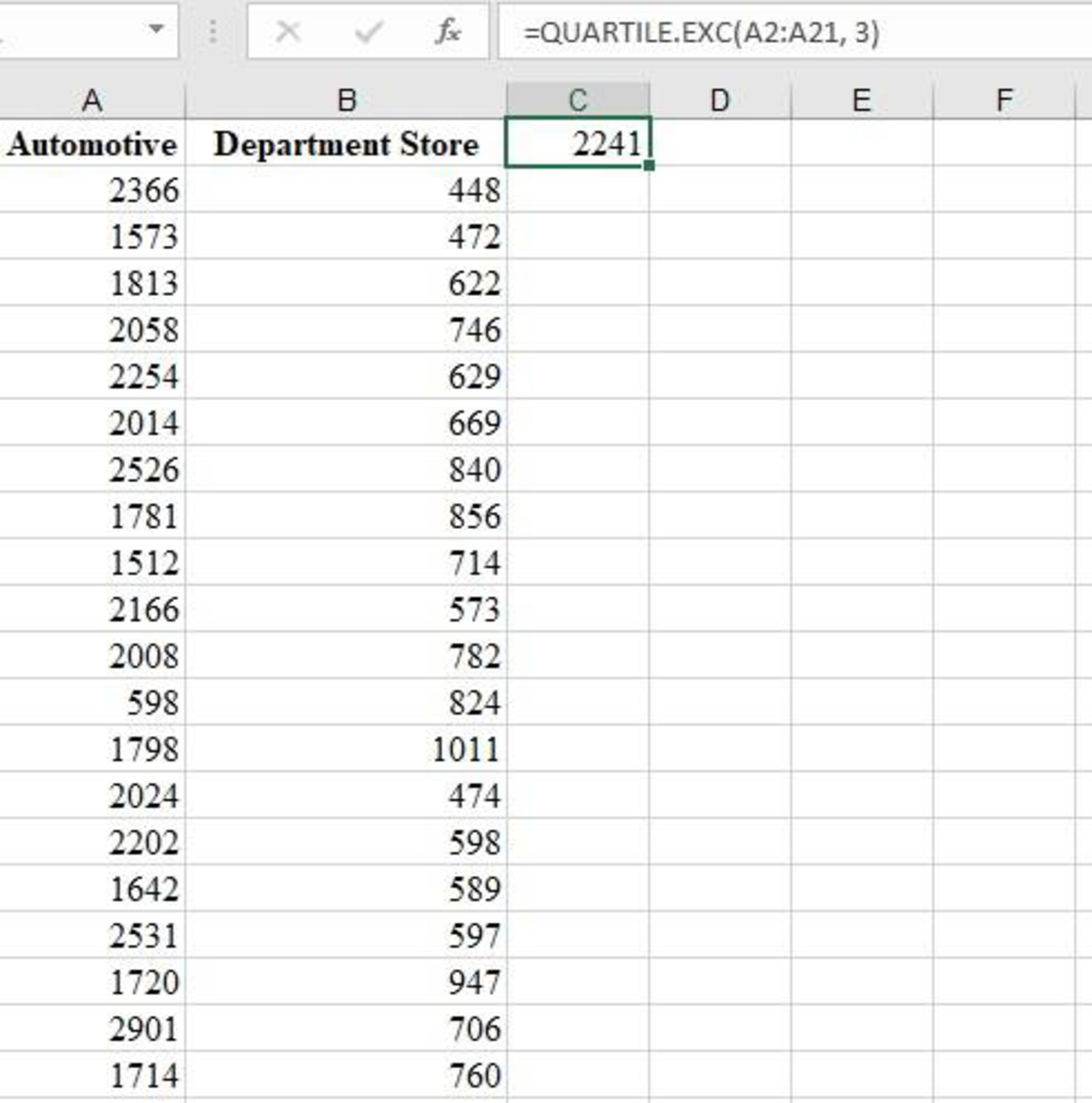
From the EXCEL output, the third quartile of the sample data is 2,241.
The first quartile, and third quartile of the sample data are 1,715.5, and 2,241, respectively.
Inter quartile range:
The first quartile is
The inter quartile range is obtained as given below:
Thus, the inter quartile range for automobile is 525.5.
Department store:
The first and third quartiles are obtained for the annual advertising expenditures in the department store sector.
First quartile:
The EXCEL function to compute first quartile is
Software Procedure:
Step by step procedure to obtain the first quartile using EXCEL is as follows:
- In an EXCEL sheet enter the values of second sample and label it as Department store.
- In a cell enter the formula QUARTILE.EXC ($B$2:$B$21,1).
- Click on OK.
Output using EXCEL is given as follows:
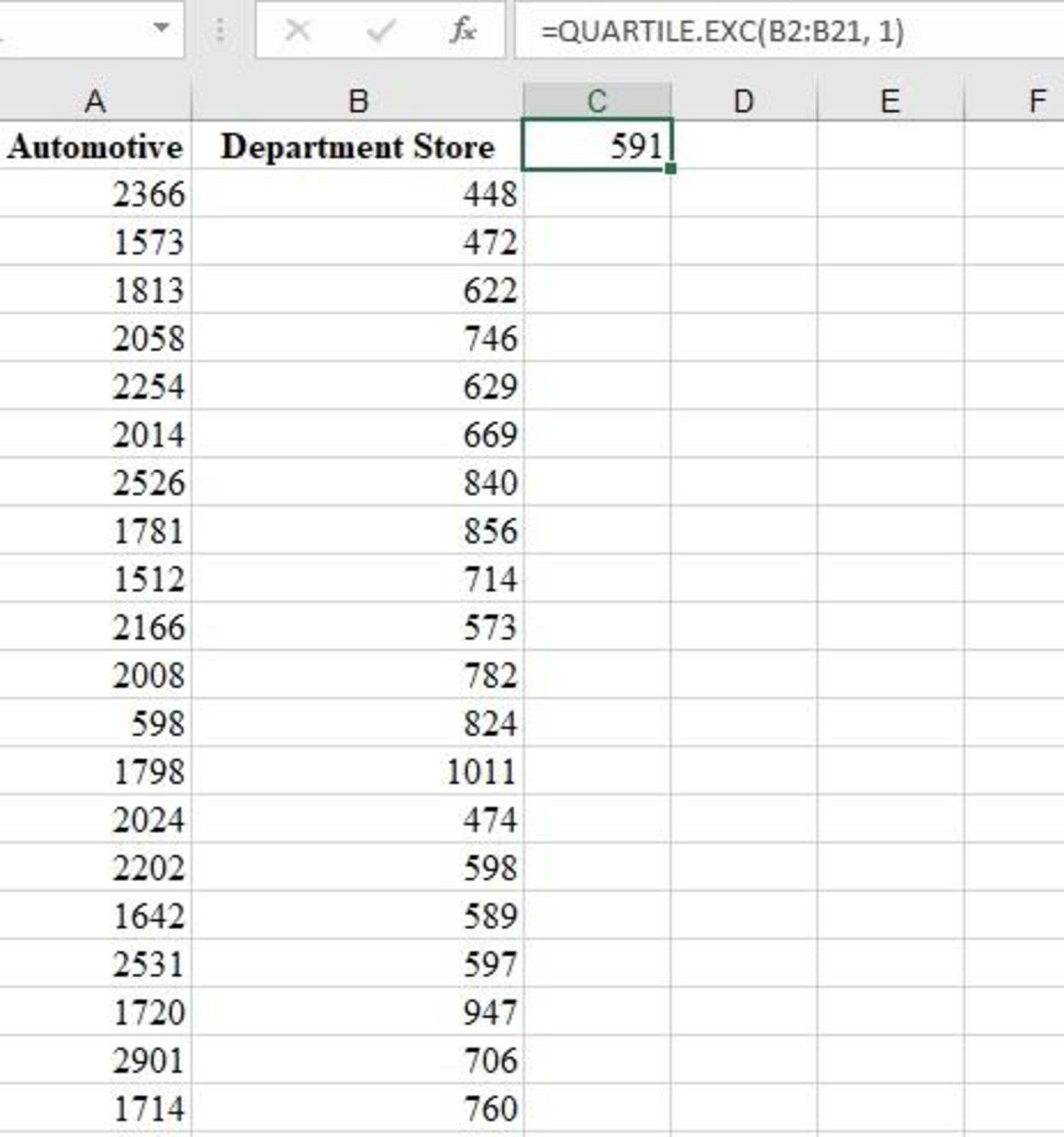
From the EXCEL output, the first quartile of the sample data is 591.
Third quartile:
The EXCEL function to compute third quartile is
Software Procedure:
Step by step procedure to obtain the third quartile using EXCEL is as follows:
- In an EXCEL sheet enter the values of second sample and label it as Department store.
- In a cell enter the formula QUARTILE.EXC ($A$2:$A$21,3).
- Click on OK.
Output using EXCEL is given as follows:
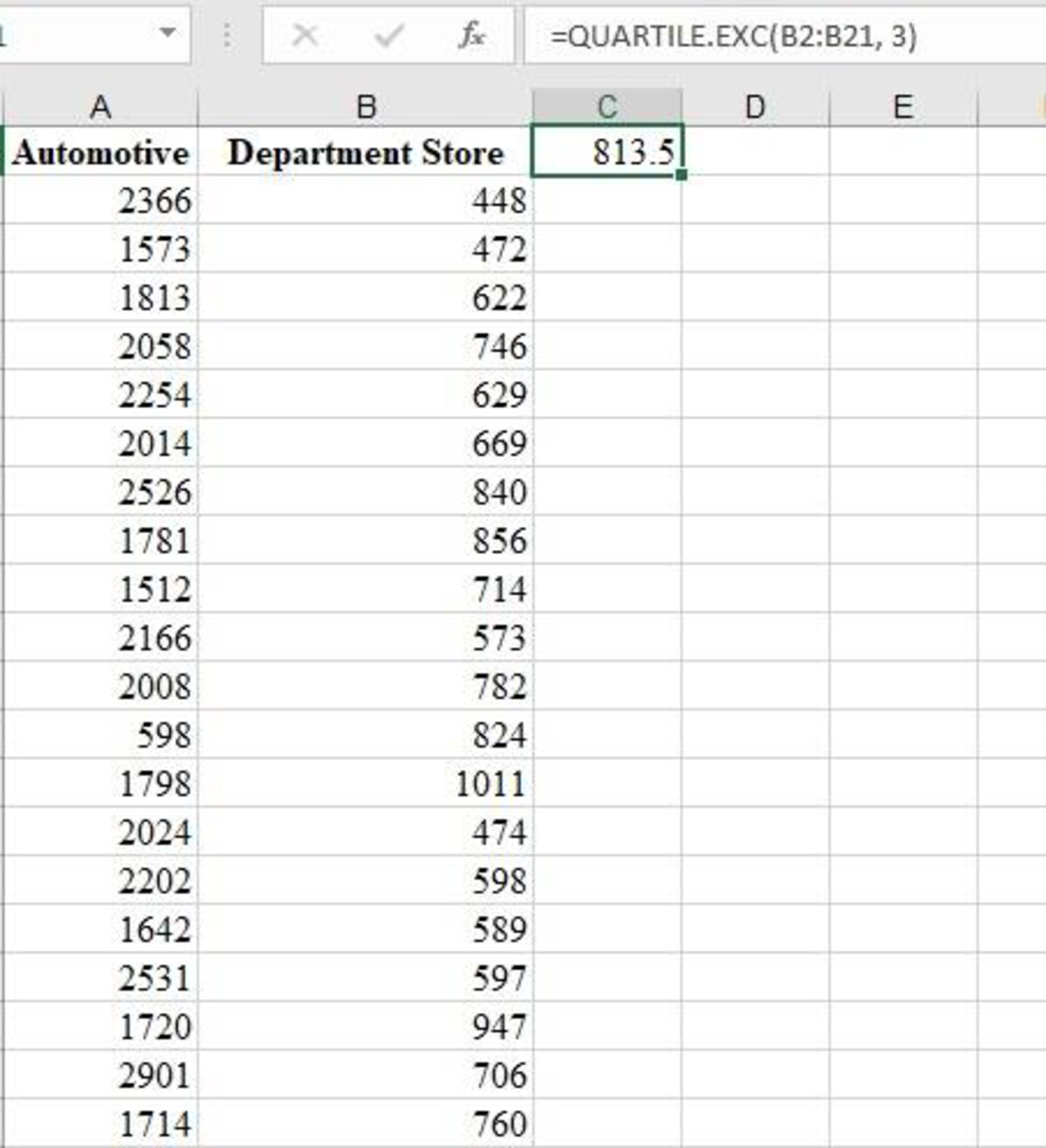
From the EXCEL output, the third quartile of the sample data is 813.5.
The first quartile, and third quartile of the sample data are 591, and 813.5, respectively.
Inter quartile range:
The first quartile is
The inter quartile range is obtained as given below:
Thus, the inter quartile range for automobile is 222.5.
Thus, the interquartile range for automotive and department store are 525.5, and 222.5, respectively.
e.
Comment on any differences in the advertising spending in the automotive companies versus the department store companies.
Explanation of Solution
The mean, standard deviation, range, and inter quartile range for annual advertising expenditure in the automotive sector are 1,960, 482, 2,303, and 525.5, respectively.
The mean, standard deviation, range, and inter quartile range for annual advertising expenditure in the department store sector are 692.85, 155.06, 563, and 222.5, respectively.
All the values of mean, standard deviation, range, and inter quartile range are higher for the annual advertising expenditure in the automotive sector than the annual advertising expenditure in the department store sector.
From this it is known that, automotive spends more money on advertising.
Want to see more full solutions like this?
Chapter 3 Solutions
Modern Business Statistics with Microsoft Office Excel (with XLSTAT Education Edition Printed Access Card) (MindTap Course List)
- There are four white, fourteen blue and five green marbles in a bag. A marble is selected from the bag without looking. Find the odds of the following: The odds against selecting a green marble. The odds in favour of not selecting a green marble The odds in favor of the marble selected being either a white or a blue marble. What is true about the above odds? Explainarrow_forwardPlease show as much work as possible to clearly show the steps you used to find each solution. If you plan to use a calculator, please be sure to clearly indicate your strategy. 1. The probability of a soccer game in a particular league going into overtime is 0.125. Find the following: a. The odds in favour of a game going into overtime. b. The odds in favour of a game not going into overtime. c. If the teams in the league play 100 games in a season, about how many games would you expect to go into overtime?arrow_forwardexplain the importance of the Hypothesis test in a business setting, and give an example of a situation where it is helpful in business decision making.arrow_forward
- A college wants to estimate what students typically spend on textbooks. A report fromthe college bookstore observes that textbooks range in price from $22 to $186. Toobtain a 95% confidence level for a confidence interval estimate to plus or minus $10,how many students should the college survey? (We may estimate the populationstandard deviation as (range) ÷ 4.)arrow_forwardIn a study of how students give directions, forty volunteers were given the task ofexplaining to another person how to reach a destination. Researchers measured thefollowing five aspects of the subjects’ direction-giving behavior:• whether a map was available or if directions were given from memory without a map,• the gender of the direction-giver,• the distances given as part of the directions,• the number of times directions such as “north” or “left” were used,• the frequency of errors in directions. Identify each of the variables in this study, and whether each is quantitative orqualitative. For each quantitative variable, state whether it is discrete or continuous. Was this an observational study or an experimental study? Explain your answer.arrow_forwardexplain the difference between the confident interval and the confident level. provide an example to show how to correctly interpret a confidence interval.arrow_forward
- Sketch to scale the orbit of Earth about the sun. Graph Icarus’ orbit on the same set of axesWhile the sun is the center of Earth’s orbit, it is a focus of Icarus’ orbit. There aretwo points of intersection on the graph. Based on the graph, what is the approximate distance between the two points of intersection (in AU)?arrow_forwardThe diameters of ball bearings are distributed normally. The mean diameter is 67 millimeters and the standard deviation is 3 millimeters. Find the probability that the diameter of a selected bearing is greater than 63 millimeters. Round to four decimal places.arrow_forwardSuppose you like to keep a jar of change on your desk. Currently, the jar contains the following: 22 Pennies 27 Dimes 9 Nickels 30 Quarters What is the probability that you reach into the jar and randomly grab a penny and then, without replacement, a dime? Express as a fraction or a decimal number rounded to four decimal places.arrow_forward
- A box contains 14 large marbles and 10 small marbles. Each marble is either green or white. 9 of the large marbles are green, and 4 of the small marbles are white. If a marble is randomly selected from the box, what is the probability that it is small or white? Express as a fraction or a decimal number rounded to four decimal places.arrow_forwardCan I get help with this step please? At a shooting range, instructors can determine if a shooter is consistently missing the target because of the gun sight or because of the shooter's ability. If a gun's sight is off, the variance of the distances between the shots and the center of the shot pattern will be small (even if the shots are not in the center of the target). A student claims that it is the sight that is off, not his aim, and wants the instructor to confirm his claim. If a skilled shooter fires a gun at a target multiple times, the distances between the shots and the center of the shot pattern, measured in centimeters (cm), will have a variance of less than 0.33. After the student shoots 28 shots at the target, the instructor calculates that the distances between his shots and the center of the shot pattern, measured in cm, have a variance of 0.25. Does this evidence support the student's claim that the gun's sight is off? Use a 0.025 level of significance. Assume that the…arrow_forwardThe National Academy of Science reported that 38% of research in mathematics is published by US authors. The mathematics chairperson of a prestigious university wishes to test the claim that this percentage is no longer 38%. He has no indication of whether the percentage has increased or decreased since that time. He surveys a simple random sample of 279 recent articles published by reputable mathematics research journals and finds that 123 of these articles have US authors. Does this evidence support the mathematics chairperson's claim that the percentage is no longer 38 % ? Use a 0.02 level of significance. Compute the value of the test statistic. Round to two decimal places.arrow_forward
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL