Elements Of Electromagnetics
7th Edition
ISBN: 9780190698614
Author: Sadiku, Matthew N. O.
Publisher: Oxford University Press
expand_more
expand_more
format_list_bulleted
Related questions
Concept explainers
Question
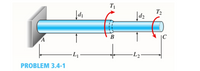
A stepped shaft ABC consisting of two solid circular segments is subjected to torques '1 and T, acting in opposite directions, as shown in the figure. The larger segment of the shaft has a diameter of d1= 2.25 in. and length L1= 30 in.;the smaller segment has a diameter of d2 1.75in. and length of L1= 20 in. The material is steel with shear modulus G = 11x 106 psi, and the torques are T1= 20.000 lb-in, and T2 8000 lb-in.
(a) Calculate the maximum shear stress tmax in the shaft and the angle of twist Φc (in degrees) at end C.
(b) If the maximum shear stress in BC must be the same as that in what is the required diameter of segment BC? What is the resulting twist at end C?
Transcribed Image Text:T2
Įd2
B
|C
-L2
PROBLEM 3.4-1
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 6 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A 3 m long steel angle shown in the figure has a section thickness of 12.7 mm and a cross sectional area of 4350 mm². Since tem = 50 MPa and G = 77.2 GPa, find the maximum applicable torque T.arrow_forwardF3.A shaft is composed of two 6-in. diameter sections coupled together (see figure below). Part AB is bronze and part BC is steel. A torque is applied at the free end which causes a maximum shear stress in the bronze shaft of 10,000 psi. Find the angle of twist of the free end. Assume the modulus of rigidity of bronze is 6 (106) psi and that of steel is 12(106) psi. Bronze Dia. = 6 in. A 3' Steel B Match each item to a choice: Angle of twist Tarrow_forwardA metal shaft ABCD with variable cross-section is subjected to three external torques (T₁=28 kip- in, T2=8 kip-in, and T3=10 kip-in) as shown in the figure below. Each torque is acting at the locations marked with circular points along the shaft. Note that a 16-inch long segment of the shaft at the free end (right) has a 1-inch diameter bore. The dimensions (lengths and diameters) of the shaft are given in the figure. Assume deformation is linear elastic and take G=12×106 psi. D [3" 16"- X C T₁ 2" -32"- T₂ 1" diam. bore B -16"- A T3 the bar has a uniform diameter d along its full length, but external torques remain the same and are applied at the same locations. If the failure shear stress for the material is equal to Tfail = 10 ksi, and the factor of safety is equal to 2, determine the required (uniform) diameter d for the bar. Assume that the bar is solid for its entire length.arrow_forward
- Two solid circular shafts (i.e., AB and BC) are fixed to rigid walls at point A and C, respectively. Members AB and BC are coupled together through a rigid plate at B. As shown in the figure, an external torque is applied at point B. Determine the absolute maximum shear stress developed in the whole structure AC. Both members AB and BC are made of the aluminum alloy with shear modulus G = 60 GPa. 150 mm 100 mm B 10 mm 5 kN-m Note: ignore the effect of stress concentration. 20 mmarrow_forwardT.L Tr4 %3D J = " (r* – rf) (Tubular shaft) Tr (Solid shaft) G.J 3. The shaft in the figure below consists of 75 mm diameter bronze segment that is rigidly joint to 50 diameter steel segment. The ends of the shaft are attached to rigid supports (fixed supports). Calculate the absolute maximum shear stress developed in each segment when the torque T= 5.1 kN-m is applied (a = 2 m and b = 1.5 m). Use G = 35 GPa for bronze, and G = 75 GPa for steel. (21 pts) 75 mm 50 mm Bronze Steelarrow_forwardA shaft ABCD is supported by a clamp at point A and is subjected to point torques at B, C and D, as shown in the figure. The shaft has variable cross-section and is solid in segments AB and CD and hollow in segment BC. The lengths and diameters of each segment are shown in the figure. Assume that the deformation is linear elastic and take the shear modulus of elasticity G = 12.1 × 10° psi. a) Using method of sections, plot the torsion moment diagram. b) Find the angle of twist for the free end (point D) with respect to the fixed support at A, QAD and the angle of twist for point C with respect to the fixed support at A, QCA. Find both angles in degrees. d₁ = 4 in d20 3.5 in, d2=2.5 in d3 = 3.0 in 25 kip-in 20 kip-in 10 kip-in A 20 in B с D ++ 25 in 30 inarrow_forward
- The shaft in Figure below consists of a 3-in. -diameter aluminum segment that is rigidly joined to a 2-in. -diameter steel segment. The ends of the shaft are attached to rigid supports, Calculate the maximum shear stress developed in each segment when the torque T= 10 kip.in is applied. Use G = 4×106 psi for aluminum and G = 12×106 psi for steel. Aluminum 3-in. diameter 6 ft T Steel 2-in. diameter 3 ftarrow_forwardA round shaft of diamater D = 65 mm with a groove cut into it where the diameter decreases to d = 50 mm. The radius of the fillet at the groove is r = %3D 2.5 mm. If the internal torsional moment at a critical cross-section in the groove is 400 N.m, calculate the maximum torsional shear stress at the groove. Round-up your answer to the nearest MPa. Max torsional shear stress MPaarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education 
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY