Precalculus with Limits: A Graphing Approach
Precalculus with Limits: A Graphing Approach
7th Edition
ISBN: 9781305071711
Author: Ron Larson
Publisher: Brooks/Cole
bartleby

Videos

Question
Book Icon
Chapter 2.8, Problem 31E
To determine

To show: The function is one to one then find its inverse function and to verify graphically.

Expert Solution & Answer
Check Mark

Answer to Problem 31E

  f−1(x)=x−52

The function is one to one.

Explanation of Solution

Given information:

  f(x)=2x+5

Formula used:

One to One: f(a)=f(b)⇒a=b for all a and b in the domain of f .

Concept used:

If a function has an inverse function, then the function is one to one.

A function is one to one graphically, if it satisfies:

  1. Horizontal line test:

    2. If a horizontal line can be drawn through the graph and the line meets the graph at only one point, the function is said to be one to one.

  2. Vertical line test:

If a vertical line can be drawn through the graph and the line meets the graph at only one point, the function is said to be one to one.

If one of these tests is true then the function is one to one.

Proof:

First part of the question is to prove one to one.

Consider the given function and substitute a and b in x .

  f(a)=2a+5f(b)=2b+5

Consider the condition for one to one and then substitute.

  f(a)=f(b)2a+5=2b+52a=2ba=b

Therefore the function is one to one.

Next part of the question is to find the inverse of the given function.

  f(x)=2x+5

Initially put f(x)=y

  ⇒y=2x+5

Interchange x and y .

  ⇒x=2y+5

Now, solve for y .

  x=2y+5x−5=2yy=x−52

Therefore, f−1(x)=x−52

Last part is to show graphically that the function is one to one.

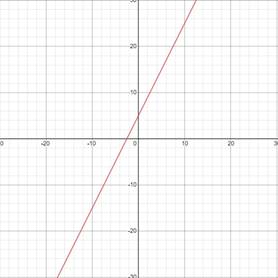
  Precalculus with Limits: A Graphing Approach, Chapter 2.8, Problem 31E

When a vertical line is drawn through this graph, it cuts the graph at only one point. Similarly, when a horizontal line is drawn through the graph, it cuts the graph at only one point.

Therefore, it is graphically proved that the function is one to one.

Previous
Chapter 2.8, Problem 30E
Next
Chapter 2.8, Problem 32E

Chapter 2 Solutions

Precalculus with Limits: A Graphing Approach

Ch. 2.1 - Prob. 1ECh. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - Prob. 9ECh. 2.1 - Prob. 10E
Ch. 2.1 - Prob. 11ECh. 2.1 - Prob. 12ECh. 2.1 - Prob. 13ECh. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - Prob. 17ECh. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - Prob. 22ECh. 2.1 - Prob. 23ECh. 2.1 - Prob. 24ECh. 2.1 - Prob. 25ECh. 2.1 - Prob. 26ECh. 2.1 - Prob. 27ECh. 2.1 - Prob. 28ECh. 2.1 - Prob. 29ECh. 2.1 - Prob. 30ECh. 2.1 - Prob. 31ECh. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Prob. 34ECh. 2.1 - Prob. 35ECh. 2.1 - Prob. 36ECh. 2.1 - Prob. 37ECh. 2.1 - Prob. 38ECh. 2.1 - Prob. 39ECh. 2.1 - Prob. 40ECh. 2.1 - Prob. 41ECh. 2.1 - Prob. 42ECh. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - Prob. 45ECh. 2.1 - Prob. 46ECh. 2.1 - Prob. 47ECh. 2.1 - Prob. 48ECh. 2.1 - Prob. 49ECh. 2.1 - Prob. 50ECh. 2.1 - Prob. 51ECh. 2.1 - Prob. 52ECh. 2.1 - Prob. 53ECh. 2.1 - Prob. 54ECh. 2.1 - Prob. 55ECh. 2.1 - Prob. 56ECh. 2.1 - Prob. 57ECh. 2.1 - Prob. 58ECh. 2.1 - Prob. 59ECh. 2.1 - Prob. 60ECh. 2.1 - Prob. 61ECh. 2.1 - Prob. 62ECh. 2.1 - Prob. 63ECh. 2.1 - Prob. 64ECh. 2.1 - Prob. 65ECh. 2.1 - Prob. 66ECh. 2.1 - Prob. 67ECh. 2.1 - Prob. 68ECh. 2.1 - Prob. 69ECh. 2.1 - Prob. 70ECh. 2.1 - Prob. 71ECh. 2.1 - Prob. 72ECh. 2.1 - Prob. 73ECh. 2.1 - Prob. 74ECh. 2.1 - Prob. 75ECh. 2.1 - Prob. 76ECh. 2.1 - Prob. 77ECh. 2.1 - Prob. 78ECh. 2.1 - Prob. 79ECh. 2.1 - Prob. 80ECh. 2.1 - Prob. 81ECh. 2.1 - Prob. 82ECh. 2.1 - Prob. 83ECh. 2.1 - Prob. 84ECh. 2.1 - Prob. 85ECh. 2.1 - Prob. 86ECh. 2.1 - Prob. 87ECh. 2.1 - Prob. 88ECh. 2.1 - Prob. 89ECh. 2.1 - Prob. 90ECh. 2.1 - Prob. 91ECh. 2.1 - Prob. 92ECh. 2.1 - Prob. 93ECh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Prob. 11ECh. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - Prob. 47ECh. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - Prob. 51ECh. 2.2 - Prob. 52ECh. 2.2 - Prob. 53ECh. 2.2 - Prob. 54ECh. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - Prob. 57ECh. 2.2 - Prob. 58ECh. 2.2 - Prob. 59ECh. 2.2 - Prob. 60ECh. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - Prob. 63ECh. 2.2 - Prob. 64ECh. 2.2 - Prob. 65ECh. 2.2 - Prob. 66ECh. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - Prob. 69ECh. 2.2 - Prob. 70ECh. 2.2 - Prob. 71ECh. 2.2 - Prob. 72ECh. 2.2 - Prob. 73ECh. 2.2 - Prob. 74ECh. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Prob. 77ECh. 2.2 - Prob. 78ECh. 2.2 - Prob. 79ECh. 2.2 - Prob. 80ECh. 2.2 - Prob. 81ECh. 2.2 - Prob. 82ECh. 2.2 - Prob. 83ECh. 2.2 - Prob. 84ECh. 2.2 - Prob. 85ECh. 2.2 - Prob. 86ECh. 2.2 - Prob. 87ECh. 2.2 - Prob. 88ECh. 2.2 - Prob. 89ECh. 2.2 - Prob. 90ECh. 2.2 - Prob. 91ECh. 2.2 - Prob. 92ECh. 2.2 - Prob. 93ECh. 2.2 - Prob. 94ECh. 2.2 - Prob. 95ECh. 2.2 - Prob. 96ECh. 2.2 - Prob. 97ECh. 2.2 - Prob. 98ECh. 2.2 - Prob. 99ECh. 2.2 - Prob. 100ECh. 2.2 - Prob. 101ECh. 2.2 - Prob. 102ECh. 2.2 - Prob. 103ECh. 2.2 - Prob. 104ECh. 2.2 - Prob. 105ECh. 2.2 - Prob. 106ECh. 2.2 - Prob. 107ECh. 2.2 - Prob. 108ECh. 2.2 - Prob. 109ECh. 2.2 - Prob. 110ECh. 2.2 - Prob. 111ECh. 2.2 - Prob. 112ECh. 2.2 - Prob. 113ECh. 2.2 - Prob. 114ECh. 2.2 - Prob. 115ECh. 2.2 - Prob. 116ECh. 2.2 - Prob. 117ECh. 2.2 - Prob. 118ECh. 2.2 - Prob. 119ECh. 2.2 - Prob. 120ECh. 2.2 - Prob. 121ECh. 2.2 - Prob. 122ECh. 2.2 - Prob. 123ECh. 2.2 - Prob. 124ECh. 2.2 - Prob. 125ECh. 2.2 - Prob. 126ECh. 2.2 - Prob. 127ECh. 2.2 - Prob. 128ECh. 2.2 - Prob. 129ECh. 2.2 - Prob. 130ECh. 2.2 - Prob. 131ECh. 2.2 - Prob. 132ECh. 2.3 - Prob. 1ECh. 2.3 - Prob. 2ECh. 2.3 - Prob. 3ECh. 2.3 - Prob. 4ECh. 2.3 - Prob. 5ECh. 2.3 - Prob. 6ECh. 2.3 - Prob. 7ECh. 2.3 - Prob. 8ECh. 2.3 - Prob. 9ECh. 2.3 - Prob. 10ECh. 2.3 - Prob. 11ECh. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - Prob. 15ECh. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - Prob. 19ECh. 2.3 - Prob. 20ECh. 2.3 - Prob. 21ECh. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - Prob. 25ECh. 2.3 - Prob. 26ECh. 2.3 - Prob. 27ECh. 2.3 - Prob. 28ECh. 2.3 - Prob. 29ECh. 2.3 - Prob. 30ECh. 2.3 - Prob. 31ECh. 2.3 - Prob. 32ECh. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Prob. 38ECh. 2.3 - Prob. 39ECh. 2.3 - Prob. 40ECh. 2.3 - Prob. 41ECh. 2.3 - Prob. 42ECh. 2.3 - Prob. 43ECh. 2.3 - Prob. 44ECh. 2.3 - Prob. 45ECh. 2.3 - Prob. 46ECh. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Prob. 49ECh. 2.3 - Prob. 50ECh. 2.3 - Prob. 51ECh. 2.3 - Prob. 52ECh. 2.3 - Prob. 53ECh. 2.3 - Prob. 54ECh. 2.3 - Prob. 55ECh. 2.3 - Prob. 56ECh. 2.3 - Prob. 57ECh. 2.3 - Prob. 58ECh. 2.3 - Prob. 59ECh. 2.3 - Prob. 60ECh. 2.3 - Prob. 61ECh. 2.3 - Prob. 62ECh. 2.3 - Prob. 63ECh. 2.3 - Prob. 64ECh. 2.3 - Prob. 65ECh. 2.3 - Prob. 66ECh. 2.3 - Prob. 67ECh. 2.3 - Prob. 68ECh. 2.3 - Prob. 69ECh. 2.3 - Prob. 70ECh. 2.3 - Prob. 71ECh. 2.3 - Prob. 72ECh. 2.3 - Prob. 73ECh. 2.3 - Prob. 74ECh. 2.3 - Prob. 75ECh. 2.3 - Prob. 76ECh. 2.3 - Prob. 77ECh. 2.3 - Prob. 78ECh. 2.3 - Prob. 79ECh. 2.3 - Prob. 80ECh. 2.3 - Prob. 81ECh. 2.3 - Prob. 82ECh. 2.3 - Prob. 83ECh. 2.3 - Prob. 84ECh. 2.3 - Prob. 85ECh. 2.3 - Prob. 86ECh. 2.3 - Prob. 87ECh. 2.3 - Prob. 88ECh. 2.3 - Prob. 89ECh. 2.3 - Prob. 90ECh. 2.3 - Prob. 91ECh. 2.3 - Prob. 92ECh. 2.3 - Prob. 93ECh. 2.3 - Prob. 94ECh. 2.3 - Prob. 95ECh. 2.3 - Prob. 96ECh. 2.3 - Prob. 97ECh. 2.3 - Prob. 98ECh. 2.3 - Prob. 99ECh. 2.3 - Prob. 100ECh. 2.3 - Prob. 101ECh. 2.3 - Prob. 102ECh. 2.3 - Prob. 103ECh. 2.3 - Prob. 104ECh. 2.3 - Prob. 105ECh. 2.3 - Prob. 106ECh. 2.3 - Prob. 107ECh. 2.3 - Prob. 108ECh. 2.3 - Prob. 109ECh. 2.3 - Prob. 110ECh. 2.3 - Prob. 111ECh. 2.3 - Prob. 112ECh. 2.3 - Prob. 113ECh. 2.3 - Prob. 114ECh. 2.3 - Prob. 115ECh. 2.3 - Prob. 116ECh. 2.3 - Prob. 117ECh. 2.3 - Prob. 118ECh. 2.3 - Prob. 119ECh. 2.3 - Prob. 120ECh. 2.4 - Prob. 1ECh. 2.4 - Prob. 2ECh. 2.4 - Prob. 3ECh. 2.4 - Prob. 4ECh. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - Prob. 18ECh. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Prob. 23ECh. 2.4 - Prob. 24ECh. 2.4 - Prob. 25ECh. 2.4 - Prob. 26ECh. 2.4 - Prob. 27ECh. 2.4 - Prob. 28ECh. 2.4 - Prob. 29ECh. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 32ECh. 2.4 - Prob. 33ECh. 2.4 - Prob. 34ECh. 2.4 - Prob. 35ECh. 2.4 - Prob. 36ECh. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.4 - Prob. 40ECh. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - Prob. 44ECh. 2.4 - Prob. 45ECh. 2.4 - Prob. 46ECh. 2.4 - Prob. 47ECh. 2.4 - Prob. 48ECh. 2.4 - Prob. 49ECh. 2.4 - Prob. 50ECh. 2.4 - Prob. 51ECh. 2.4 - Prob. 52ECh. 2.4 - Prob. 53ECh. 2.4 - Prob. 54ECh. 2.4 - Prob. 55ECh. 2.4 - Prob. 56ECh. 2.4 - Prob. 57ECh. 2.4 - Prob. 58ECh. 2.4 - Prob. 59ECh. 2.4 - Prob. 60ECh. 2.4 - Prob. 61ECh. 2.4 - Prob. 62ECh. 2.4 - Prob. 63ECh. 2.4 - Prob. 64ECh. 2.4 - Prob. 65ECh. 2.4 - Prob. 66ECh. 2.4 - Prob. 67ECh. 2.4 - Prob. 68ECh. 2.4 - Prob. 69ECh. 2.4 - Prob. 70ECh. 2.4 - Prob. 71ECh. 2.4 - Prob. 72ECh. 2.4 - Prob. 73ECh. 2.4 - Prob. 74ECh. 2.4 - Prob. 75ECh. 2.4 - Prob. 76ECh. 2.4 - Prob. 77ECh. 2.4 - Prob. 78ECh. 2.4 - Prob. 79ECh. 2.4 - Prob. 80ECh. 2.4 - Prob. 81ECh. 2.4 - Prob. 82ECh. 2.4 - Prob. 83ECh. 2.4 - Prob. 84ECh. 2.4 - Prob. 85ECh. 2.4 - Prob. 86ECh. 2.4 - Prob. 87ECh. 2.4 - Prob. 88ECh. 2.4 - Prob. 89ECh. 2.4 - Prob. 90ECh. 2.4 - Prob. 91ECh. 2.4 - Prob. 92ECh. 2.4 - Prob. 93ECh. 2.4 - Prob. 94ECh. 2.4 - Prob. 95ECh. 2.4 - Prob. 96ECh. 2.4 - Prob. 97ECh. 2.4 - Prob. 98ECh. 2.4 - Prob. 99ECh. 2.4 - Prob. 100ECh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.5 - Prob. 5ECh. 2.5 - Prob. 6ECh. 2.5 - Prob. 7ECh. 2.5 - Prob. 8ECh. 2.5 - Prob. 9ECh. 2.5 - Prob. 10ECh. 2.5 - Prob. 11ECh. 2.5 - Prob. 12ECh. 2.5 - Prob. 13ECh. 2.5 - Prob. 14ECh. 2.5 - Prob. 15ECh. 2.5 - Prob. 16ECh. 2.5 - Prob. 17ECh. 2.5 - Prob. 18ECh. 2.5 - Prob. 19ECh. 2.5 - Prob. 20ECh. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Prob. 27ECh. 2.5 - Prob. 28ECh. 2.5 - Prob. 29ECh. 2.5 - Prob. 30ECh. 2.5 - Prob. 31ECh. 2.5 - Prob. 32ECh. 2.5 - Prob. 33ECh. 2.5 - Prob. 34ECh. 2.5 - Prob. 35ECh. 2.5 - Prob. 36ECh. 2.5 - Prob. 37ECh. 2.5 - Prob. 38ECh. 2.5 - Prob. 39ECh. 2.5 - Prob. 40ECh. 2.5 - Prob. 41ECh. 2.5 - Prob. 42ECh. 2.5 - Prob. 43ECh. 2.5 - Prob. 44ECh. 2.5 - Prob. 45ECh. 2.5 - Prob. 46ECh. 2.5 - Prob. 47ECh. 2.5 - Prob. 48ECh. 2.5 - Prob. 49ECh. 2.5 - Prob. 50ECh. 2.5 - Prob. 51ECh. 2.5 - Prob. 52ECh. 2.5 - Prob. 53ECh. 2.5 - Prob. 54ECh. 2.5 - Prob. 55ECh. 2.5 - Prob. 56ECh. 2.5 - Prob. 57ECh. 2.5 - Prob. 58ECh. 2.5 - Prob. 59ECh. 2.5 - Prob. 60ECh. 2.5 - Prob. 61ECh. 2.5 - Prob. 62ECh. 2.5 - Prob. 63ECh. 2.5 - Prob. 64ECh. 2.5 - Prob. 65ECh. 2.5 - Prob. 66ECh. 2.5 - Prob. 67ECh. 2.5 - Prob. 68ECh. 2.5 - Prob. 69ECh. 2.5 - Prob. 70ECh. 2.5 - Prob. 71ECh. 2.5 - Prob. 72ECh. 2.5 - Prob. 73ECh. 2.5 - Prob. 74ECh. 2.5 - Prob. 75ECh. 2.5 - Prob. 76ECh. 2.5 - Prob. 77ECh. 2.5 - Prob. 78ECh. 2.6 - Prob. 1ECh. 2.6 - Prob. 2ECh. 2.6 - Prob. 3ECh. 2.6 - Prob. 4ECh. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Prob. 16ECh. 2.6 - Prob. 17ECh. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - Prob. 23ECh. 2.6 - Prob. 24ECh. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - Prob. 31ECh. 2.6 - Prob. 32ECh. 2.6 - Prob. 33ECh. 2.6 - Prob. 34ECh. 2.6 - Prob. 35ECh. 2.6 - Prob. 36ECh. 2.6 - Prob. 37ECh. 2.6 - Prob. 38ECh. 2.6 - Prob. 39ECh. 2.6 - Prob. 40ECh. 2.6 - Prob. 41ECh. 2.6 - Prob. 42ECh. 2.6 - Prob. 43ECh. 2.6 - Prob. 44ECh. 2.6 - Prob. 45ECh. 2.6 - Prob. 46ECh. 2.6 - Prob. 47ECh. 2.6 - Prob. 48ECh. 2.6 - Prob. 49ECh. 2.6 - Prob. 50ECh. 2.6 - Prob. 51ECh. 2.6 - Prob. 52ECh. 2.6 - Prob. 53ECh. 2.6 - Prob. 54ECh. 2.6 - Prob. 55ECh. 2.6 - Prob. 56ECh. 2.6 - Prob. 57ECh. 2.6 - Prob. 58ECh. 2.6 - Prob. 59ECh. 2.6 - Prob. 60ECh. 2.6 - Prob. 61ECh. 2.6 - Prob. 62ECh. 2.6 - Prob. 63ECh. 2.6 - Prob. 64ECh. 2.7 - Prob. 1ECh. 2.7 - Prob. 2ECh. 2.7 - Prob. 3ECh. 2.7 - Prob. 4ECh. 2.7 - Prob. 5ECh. 2.7 - Prob. 6ECh. 2.7 - Prob. 7ECh. 2.7 - Prob. 8ECh. 2.7 - Prob. 9ECh. 2.7 - Prob. 10ECh. 2.7 - Prob. 11ECh. 2.7 - Prob. 12ECh. 2.7 - Prob. 13ECh. 2.7 - Prob. 14ECh. 2.7 - Prob. 15ECh. 2.7 - Prob. 16ECh. 2.7 - Prob. 17ECh. 2.7 - Prob. 18ECh. 2.7 - Prob. 19ECh. 2.7 - Prob. 20ECh. 2.7 - Prob. 21ECh. 2.7 - Prob. 22ECh. 2.7 - Prob. 23ECh. 2.7 - Prob. 24ECh. 2.7 - Prob. 25ECh. 2.7 - Prob. 26ECh. 2.7 - Prob. 27ECh. 2.7 - Prob. 28ECh. 2.7 - Prob. 29ECh. 2.7 - Prob. 30ECh. 2.7 - Prob. 31ECh. 2.7 - Prob. 32ECh. 2.7 - Prob. 33ECh. 2.7 - Prob. 34ECh. 2.7 - Prob. 35ECh. 2.7 - Prob. 36ECh. 2.7 - Prob. 37ECh. 2.7 - Prob. 38ECh. 2.7 - Prob. 39ECh. 2.7 - Prob. 40ECh. 2.7 - Prob. 41ECh. 2.7 - Prob. 42ECh. 2.7 - Prob. 43ECh. 2.7 - Prob. 44ECh. 2.7 - Prob. 45ECh. 2.7 - Prob. 46ECh. 2.7 - Prob. 47ECh. 2.7 - Prob. 48ECh. 2.7 - Prob. 49ECh. 2.7 - Prob. 50ECh. 2.7 - Prob. 51ECh. 2.7 - Prob. 52ECh. 2.7 - Prob. 53ECh. 2.7 - Prob. 54ECh. 2.7 - Prob. 55ECh. 2.7 - Prob. 56ECh. 2.7 - Prob. 57ECh. 2.7 - Prob. 58ECh. 2.7 - Prob. 59ECh. 2.7 - Prob. 60ECh. 2.7 - Prob. 61ECh. 2.7 - Prob. 62ECh. 2.7 - Prob. 63ECh. 2.7 - Prob. 64ECh. 2.7 - Prob. 65ECh. 2.7 - Prob. 66ECh. 2.7 - Prob. 67ECh. 2.7 - Prob. 68ECh. 2.7 - Prob. 69ECh. 2.7 - Prob. 70ECh. 2.7 - Prob. 71ECh. 2.7 - Prob. 72ECh. 2.7 - Prob. 73ECh. 2.7 - Prob. 74ECh. 2.7 - Prob. 75ECh. 2.7 - Prob. 76ECh. 2.7 - Prob. 77ECh. 2.7 - Prob. 78ECh. 2.7 - Prob. 79ECh. 2.7 - Prob. 80ECh. 2.7 - Prob. 81ECh. 2.7 - Prob. 82ECh. 2.7 - Prob. 83ECh. 2.7 - Prob. 84ECh. 2.7 - Prob. 85ECh. 2.7 - Prob. 86ECh. 2.7 - Prob. 87ECh. 2.7 - Prob. 88ECh. 2.7 - Prob. 89ECh. 2.7 - Prob. 90ECh. 2.7 - Prob. 91ECh. 2.7 - Prob. 92ECh. 2.7 - Prob. 93ECh. 2.7 - Prob. 94ECh. 2.7 - Prob. 95ECh. 2.7 - Prob. 96ECh. 2.7 - Prob. 97ECh. 2.7 - Prob. 98ECh. 2.7 - Prob. 99ECh. 2.7 - Prob. 100ECh. 2.7 - Prob. 101ECh. 2.7 - Prob. 102ECh. 2.7 - Prob. 103ECh. 2.7 - Prob. 104ECh. 2.7 - Prob. 105ECh. 2.7 - Prob. 106ECh. 2.7 - Prob. 107ECh. 2.8 - Prob. 1ECh. 2.8 - Prob. 2ECh. 2.8 - Prob. 3ECh. 2.8 - Prob. 4ECh. 2.8 - Prob. 5ECh. 2.8 - Prob. 6ECh. 2.8 - Prob. 7ECh. 2.8 - Prob. 8ECh. 2.8 - Prob. 9ECh. 2.8 - Prob. 10ECh. 2.8 - Prob. 11ECh. 2.8 - Prob. 12ECh. 2.8 - Prob. 13ECh. 2.8 - Prob. 14ECh. 2.8 - Prob. 15ECh. 2.8 - Prob. 16ECh. 2.8 - Prob. 17ECh. 2.8 - Prob. 18ECh. 2.8 - Prob. 19ECh. 2.8 - Prob. 20ECh. 2.8 - Prob. 21ECh. 2.8 - Prob. 22ECh. 2.8 - Prob. 23ECh. 2.8 - Prob. 24ECh. 2.8 - Prob. 25ECh. 2.8 - Prob. 26ECh. 2.8 - Prob. 27ECh. 2.8 - Prob. 28ECh. 2.8 - Prob. 29ECh. 2.8 - Prob. 30ECh. 2.8 - Prob. 31ECh. 2.8 - Prob. 32ECh. 2.8 - Prob. 33ECh. 2.8 - Prob. 34ECh. 2.8 - Prob. 35ECh. 2.8 - Prob. 36ECh. 2.8 - Prob. 37ECh. 2.8 - Prob. 38ECh. 2 - Prob. 1RECh. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - Prob. 15RECh. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - Prob. 21RECh. 2 - Prob. 22RECh. 2 - Prob. 23RECh. 2 - Prob. 24RECh. 2 - Prob. 25RECh. 2 - Prob. 26RECh. 2 - Prob. 27RECh. 2 - Prob. 28RECh. 2 - Prob. 29RECh. 2 - Prob. 30RECh. 2 - Prob. 31RECh. 2 - Prob. 32RECh. 2 - Prob. 33RECh. 2 - Prob. 34RECh. 2 - Prob. 35RECh. 2 - Prob. 36RECh. 2 - Prob. 37RECh. 2 - Prob. 38RECh. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 46RECh. 2 - Prob. 47RECh. 2 - Prob. 48RECh. 2 - Prob. 49RECh. 2 - Prob. 50RECh. 2 - Prob. 51RECh. 2 - Prob. 52RECh. 2 - Prob. 53RECh. 2 - Prob. 54RECh. 2 - Prob. 55RECh. 2 - Prob. 56RECh. 2 - Prob. 57RECh. 2 - Prob. 58RECh. 2 - Prob. 59RECh. 2 - Prob. 60RECh. 2 - Prob. 61RECh. 2 - Prob. 62RECh. 2 - Prob. 63RECh. 2 - Prob. 64RECh. 2 - Prob. 65RECh. 2 - Prob. 66RECh. 2 - Prob. 67RECh. 2 - Prob. 68RECh. 2 - Prob. 69RECh. 2 - Prob. 70RECh. 2 - Prob. 71RECh. 2 - Prob. 72RECh. 2 - Prob. 73RECh. 2 - Prob. 74RECh. 2 - Prob. 75RECh. 2 - Prob. 76RECh. 2 - Prob. 77RECh. 2 - Prob. 78RECh. 2 - Prob. 79RECh. 2 - Prob. 80RECh. 2 - Prob. 81RECh. 2 - Prob. 82RECh. 2 - Prob. 83RECh. 2 - Prob. 84RECh. 2 - Prob. 85RECh. 2 - Prob. 86RECh. 2 - Prob. 87RECh. 2 - Prob. 88RECh. 2 - Prob. 89RECh. 2 - Prob. 90RECh. 2 - Prob. 91RECh. 2 - Prob. 92RECh. 2 - Prob. 93RECh. 2 - Prob. 94RECh. 2 - Prob. 95RECh. 2 - Prob. 96RECh. 2 - Prob. 97RECh. 2 - Prob. 98RECh. 2 - Prob. 99RECh. 2 - Prob. 100RECh. 2 - Prob. 101RECh. 2 - Prob. 102RECh. 2 - Prob. 103RECh. 2 - Prob. 104RECh. 2 - Prob. 105RECh. 2 - Prob. 106RECh. 2 - Prob. 107RECh. 2 - Prob. 108RECh. 2 - Prob. 109RECh. 2 - Prob. 110RECh. 2 - Prob. 111RECh. 2 - Prob. 112RECh. 2 - Prob. 113RECh. 2 - Prob. 114RECh. 2 - Prob. 115RECh. 2 - Prob. 116RECh. 2 - Prob. 117RECh. 2 - Prob. 118RECh. 2 - Prob. 119RECh. 2 - Prob. 120RECh. 2 - Prob. 121RECh. 2 - Prob. 122RECh. 2 - Prob. 123RECh. 2 - Prob. 124RECh. 2 - Prob. 125RECh. 2 - Prob. 126RECh. 2 - Prob. 127RECh. 2 - Prob. 128RECh. 2 - Prob. 129RECh. 2 - Prob. 130RECh. 2 - Prob. 131RECh. 2 - Prob. 132RECh. 2 - Prob. 133RECh. 2 - Prob. 134RECh. 2 - Prob. 135RECh. 2 - Prob. 136RECh. 2 - Prob. 137RECh. 2 - Prob. 138RECh. 2 - Prob. 139RECh. 2 - Prob. 140RECh. 2 - Prob. 141RECh. 2 - Prob. 142RECh. 2 - Prob. 143RECh. 2 - Prob. 144RECh. 2 - Prob. 145RECh. 2 - Prob. 146RECh. 2 - Prob. 147RECh. 2 - Prob. 148RECh. 2 - Prob. 149RECh. 2 - Prob. 150RECh. 2 - Prob. 151RECh. 2 - Prob. 152RECh. 2 - Prob. 153RECh. 2 - Prob. 154RECh. 2 - Prob. 155RECh. 2 - Prob. 156RECh. 2 - Prob. 157RECh. 2 - Prob. 158RECh. 2 - Prob. 159RECh. 2 - Prob. 160RECh. 2 - Prob. 161RECh. 2 - Prob. 162RECh. 2 - Prob. 163RECh. 2 - Prob. 164RECh. 2 - Prob. 165RECh. 2 - Prob. 166RECh. 2 - Prob. 167RECh. 2 - Prob. 168RECh. 2 - Prob. 1CTCh. 2 - Prob. 2CTCh. 2 - Prob. 3CTCh. 2 - Prob. 4CTCh. 2 - Prob. 5CTCh. 2 - Prob. 6CTCh. 2 - Prob. 7CTCh. 2 - Prob. 8CTCh. 2 - Prob. 9CTCh. 2 - Prob. 10CTCh. 2 - Prob. 11CTCh. 2 - Prob. 12CTCh. 2 - Prob. 13CTCh. 2 - Prob. 14CTCh. 2 - Prob. 15CTCh. 2 - Prob. 16CTCh. 2 - Prob. 17CTCh. 2 - Prob. 18CTCh. 2 - Prob. 19CTCh. 2 - Prob. 20CTCh. 2 - Prob. 21CTCh. 2 - Prob. 22CTCh. 2 - Prob. 23CT
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=_niP0JaOgHY;License: Standard YouTube License, CC-BY