Chapter 2.5, Problem 32E

To determine

Find the zeros of the function $f(x)=x^3+11x^2+39x+29$ and write the polynomial as a product of linear factors and verify zeros using graphical method.

Answer to Problem 32E

  $-1,-5+2i,-5-2i.$

Explanation of Solution

Given:

Function: $f(x)=x^3+11x^2+39x+29$

Calculation:

The leading coefficient of given polynomial is 1 and the constant term is 29.

So, possible rational zeros are: $\frac{\text{Factors of}29}{\text{Factors of 1}}=\frac{\pm 1,\pm 29}{\pm 1}=\pm 1,\pm 29$

Using synthetic division to check whether $x=-1$ , is a zero or not.

  $\begin{array}{ccccc}-1& 1& 11& 39& 29\\ & & -1& -10& -29\\ & 1& 10& 29& \boxed{0}\end{array}\begin{array}{c}\\ \\ \hspace{1em}\leftarrow \text{Remainder}\end{array}$

Here, remainder is 0. So, $x=-1$ is a zero of the given polynomial.

So, $f(x)$ factors as

  $f(x)=\left(x+1\right)(x^2+10x+29)$

Now, consider $x^2+10x+29.$

The above polynomial is a second degree polynomial.

So, zeroes of a second degree polynomial can be found using the formula $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.$

  $\begin{array}{l}\Rightarrow x=\frac{-10\pm \sqrt{{(10)}^2-4(1)(29)}}{2(1)}\\ \Rightarrow x=\frac{-10\pm \sqrt{100-116}}{2}\\ \Rightarrow x=\frac{-10\pm \sqrt{-16}}{2}\\ \Rightarrow x=\frac{-10\pm 4\sqrt{-1}}{2}\\ \Rightarrow x=\frac{-10\pm 4i}{2}\\ \Rightarrow x=-5\pm 2i\\ \Rightarrow x=-5+2i,-5-2i\end{array}$

Now, writing the given function as product of linear factors,

  $\Rightarrow f(x)=\left(x+1\right)\left(x-(-5+2i)\right)\left(x-(-5-2i)\right)$

Calculation for graph:

Consider $f(x)=x^3+11x^2+39x+29$

Values of x	Values of f (x)
0	29
1	80
-1	0
2	159
-2	-13

By taking different values of x, the graph can be plotted.

Graph:

  

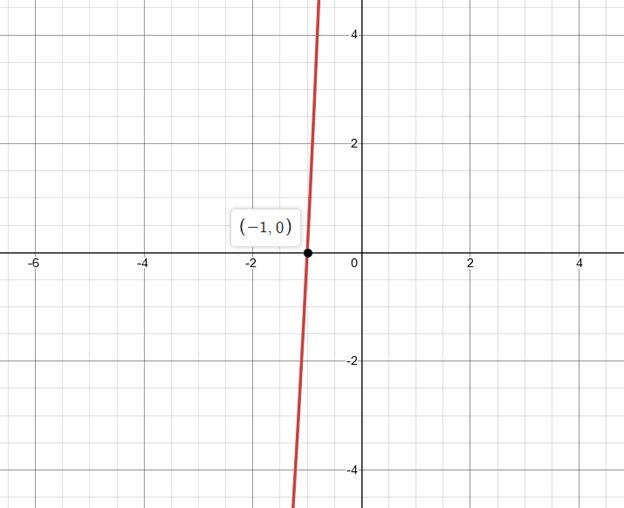
Interpretation:

Only real zeros of the function can be verified through graph.

By observing graph, it is clear that the curve of the function meets x-axis at

  $x=-1.$

Hence, the real zeros of the function are $x=-1.$

Conclusion:

Therefore, the zeros of given function are $x=-1,-5+2i\text{and}-5-2i.$