Chapter 2.5, Problem 35E

To determine

Find the zeros of the function $g(x)=x^4-4x^3+8x^2-16x+16$ and write the polynomial as a product of linear factors and verify zeros using graphical method.

Answer to Problem 35E

  $2,2,2i,-2i$

Explanation of Solution

Given:

Function: $g(x)=x^4-4x^3+8x^2-16x+16$

Calculation:

The leading coefficient of given polynomial is 1 and the constant term is 16.

So, possible rational zeros are: $\frac{\text{Factors of}16}{\text{Factors of 1}}=\frac{\pm 1,\pm 2,\pm 4,\pm 8,\pm 16}{\pm 1}=\pm 1,\pm 2,\pm 4,\pm 8,\pm 16$

Using synthetic division to check whether $x=2$ , is a zero or not.

  $\begin{array}{cccccc}2& 1& -4& 8& -16& 16\\ & & 2& -4& 8& -16\\ & 1& -2& 4& -8& \boxed{0}\end{array}\begin{array}{c}\\ \\ \hspace{1em}\leftarrow \text{Remainder}\end{array}$

Here, remainder is 0. So, $x=2$ is a zero of the given polynomial.

So, $g(x)$ factors as

  $g(x)=\left(x-2\right)(x^3-2x^2+4x-8)$

Now, consider $x^3-2x^2+4x-8.$

The leading coefficient of given polynomial is 1 and the constant term is -8.

So, possible rational zeros are: $\frac{\text{Factors of}-8}{\text{Factors of 1}}=\frac{\pm 1,\pm 2,\pm 4,\pm 8}{\pm 1}=\pm 1,\pm 2,\pm 4,\pm 8$

Using synthetic division to check whether $x=2$ , is a zero or not.

  $\begin{array}{ccccc}2& 1& -2& 4& -8\\ & & 2& 0& 8\\ & 1& 0& 4& \boxed{0}\end{array}\begin{array}{c}\\ \\ \hspace{1em}\leftarrow \text{Remainder}\end{array}$

Here, remainder is 0. So, $x=2$ is a zero of the given polynomial.

So, $g(x)$ factors as

  $g(x)=\left(x-2\right)(x-2)(x^2+4)$

Now, consider $x^2+4.$

The above polynomial is a second degree polynomial.

So, zeroes of a second degree polynomial can be found using the formula $x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.$

  $\begin{array}{l}\Rightarrow x=\frac{-0\pm \sqrt{{(0)}^2-4(1)(4)}}{2(1)}\\ \Rightarrow x=\frac{0\pm \sqrt{0-16}}{2}\\ \Rightarrow x=\frac{\pm \sqrt{-16}}{2}\\ \Rightarrow x=\frac{\pm 4\sqrt{-1}}{2}\\ \Rightarrow x=\pm 2i\\ \Rightarrow x=2i,-2i\end{array}$

Now, writing the given function as product of linear factors,

  $\Rightarrow g(x)=\left(x-2\right)(x-2)\left(x-2i\right)\left(x+2i\right)$

Calculation for graph:

Consider $g(x)=x^4-4x^3+8x^2-16x+16$

Values of x	Values of g(x)
0	16
1	5
-1	45
2	0
-2	128

By taking different values of x, the graph can be plotted.

Graph:

  

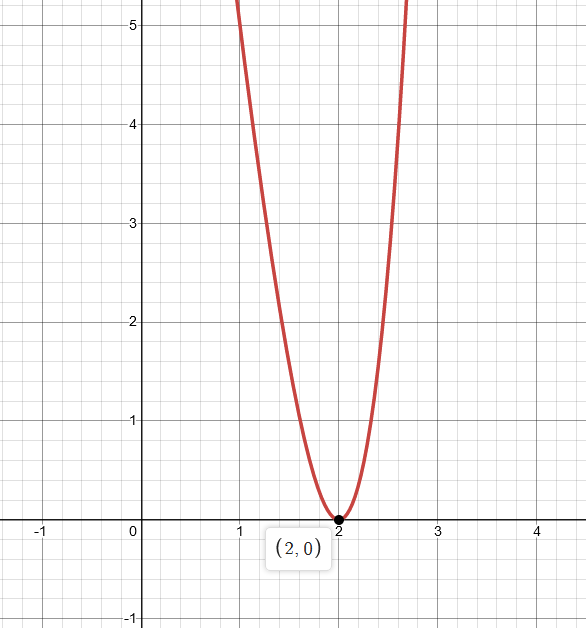
Interpretation:

Only real zeros of the function can be verified through graph.

By observing graph, it is clear that the curve of the function meets x-axis at

  $x=2.$

Hence, the real zeros of the function are $x=2.$

Conclusion:

Therefore, the zeros of given function are $x=2,2,2i\text{and}-2i.$