
Concept explainers
a.
To find:The interval of unit length in which zero of the given polynomial function lie definitely, using Intermediate Value Theorem and graphing utility.
a.
Answer to Problem 100E
The required intervals are
Explanation of Solution
Given:
The polynomial function is
Formula/ concept used:
The Intermediate Value Theorem states that
Graph:
The graph of function
We have
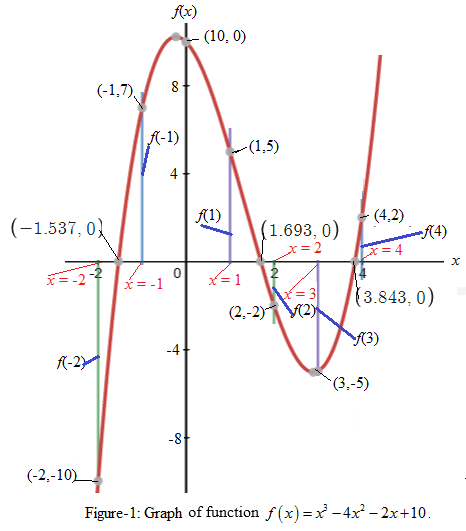
We have
We have
Conclusion:
There exists a zero of
b.
To find: The real zeros of polynomial function given in part (a) using graphing utility.
b.
Answer to Problem 100E
The zeros of function
Explanation of Solution
Given:
The polynomial function and the graph of function
Concept used:
The value of x where the graph of function intersect or touch the x -axis is the zero of function.
Calculations:
From graph Figure-1, in part (a) we see that graph of function
Hence,
Conclusion:
The points
c.
To verify: The answers of part (a) using table feature of graphing utility.
c.
Explanation of Solution
Given:
The zeros of function
Verification:
From the graph in Figure-1, we obtain a table of some solutions of the given polynomial function

There is change of the function
Thus, the results of part (a) stands verified.
Chapter 2 Solutions
Precalculus with Limits: A Graphing Approach
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





