Chapter 14, Problem 27PQ

Children playing pirates have suspended a uniform wooden plank with mass 15.0 kg and length 2.50 m as shown in Figure P14.27. What is the tension in each of the three ropes when Sophia, with a mass of 23.0 kg, is made to “walk the plank” and is 1.50 m from reaching the end of the plank?

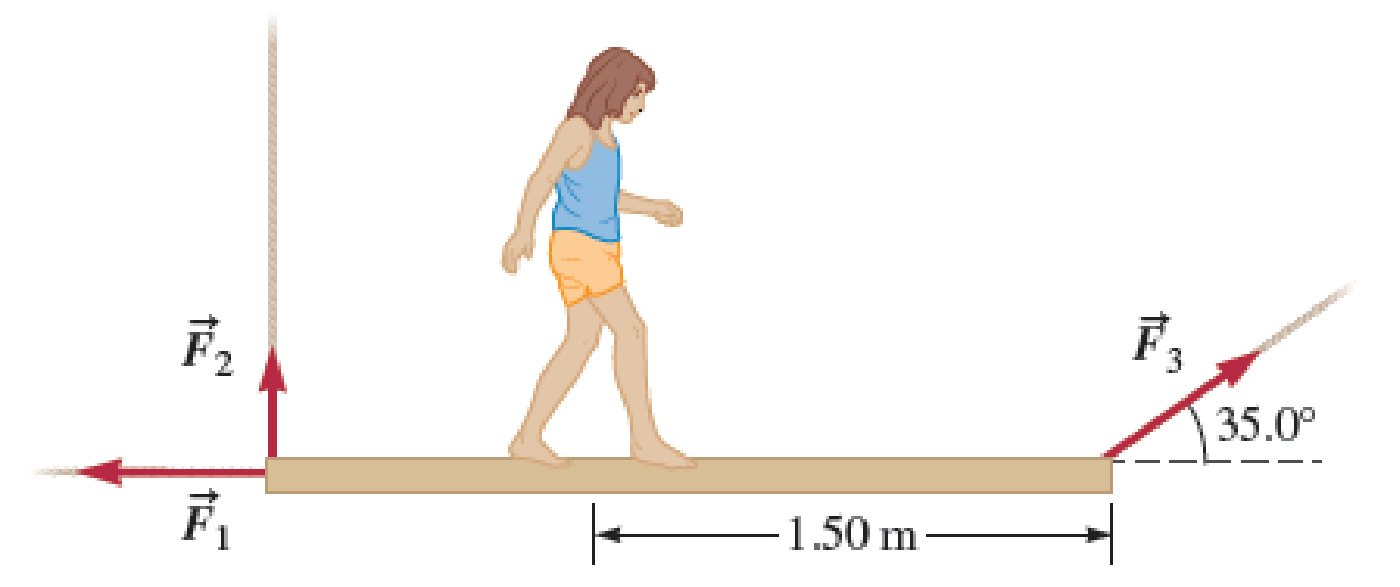
FIGURE P14.27

To determine

The tension in each of the three ropes when S with mass of $23.0\text{kg}$, is made to “walk the plank” and is $1.50\text{m}$ from reaching the end of the plank.

Answer to Problem 27PQ

The tension in rope1 is $F_1=234\text{N}$, tension in rope2 is $F_2=209\text{N}$ and tension in rope3 is $F_3=286\text{N}$ .

Explanation of Solution

The free body diagram is given below.

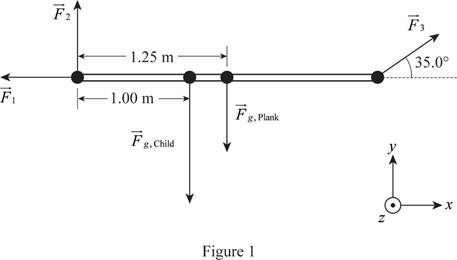
Here, ${\overrightarrow{\text{F}}}_1$ is the tension in rope1, ${\overrightarrow{\text{F}}}_2$ is the tension in rope2, ${\overrightarrow{\text{F}}}_3$ is the tension in rope 3, ${\overrightarrow{\text{F}}}_{g,\text{Child}}$ is the weight of S and ${\overrightarrow{\text{F}}}_{g.\text{Plank}}$ is the weight of Plank.

At equilibrium, the sum of forces and sum of torques must be zero.

Consider torque about an axis perpendicular to the page and through the left end of the plank.

Write the equilibrium condition for the torque about an axis perpendicular to the page and through the left end of the plank.

  $\Sigma \tau =0$                                                                                                                      (I)

Here, $\Sigma \tau$ is the torque about an axis perpendicular to the page and through the left end of the plank.

Since forces ${\overrightarrow{\text{F}}}_1$ and ${\overrightarrow{\text{F}}}_2$ are acting at axis about which torque is to be calculated, they does not produce torque on the plank.

Write the expression for the torque due to a force.

  $\tau =Fr\sin \varphi$

Here, $\tau$ is the torque, $F$ is the magnitude of force, $r$ is the perpendicular distance between force and point of rotation and $\varphi$ is the angle between force and position vector of point where force is acting.

The forces ${\overrightarrow{\text{F}}}_{g,\text{Child}}$ and ${\overrightarrow{\text{F}}}_{g.\text{Plank}}$ are making $90°$ with position vector whereas ${\overrightarrow{\text{F}}}_3$ makes an angle as shown in figure1.

Write expression for the net torque about an axis perpendicular to the page and through the left end of the plank.

  $\Sigma \tau =F_{g,\text{Child}}{r}_{\text{child}}+F_{g.\text{Plank}}{r}_{\text{plank}}+\left(F_3\sin \theta \right)r_3$                                                              (II)

Here, $F_{g,\text{Child}}$ is the weight of S, $r_{\text{child}}$ is the perpendicular distance between ${\overrightarrow{\text{F}}}_{g,\text{Child}}$ and axis , $F_{g.\text{Plank}}$ is the weight of plank , $r_{\text{plank}}$ is the perpendicular distance between ${\overrightarrow{\text{F}}}_{g.\text{Plank}}$ and axis , $F_3$ is the magnitude of force on rope as shown in figure, $\theta$ is the angle that ${\overrightarrow{\text{F}}}_3$ makes with horizontal and $r_3$ is the distance between point where ${\overrightarrow{\text{F}}}_3$ acts and axis.

Write the expression for $F_{g,\text{Child}}$.

  $F_{g,\text{Child}}=m_{\text{child}}g$                                                                                                       (III)

Here, $m_{\text{child}}$ is the mass of S and $g$ is the acceleration due to gravity.

Write the expression for $F_{g,\text{Plank}}$.

  $F_{g,\text{Plank}}=m_{\text{Plank}}g$                                                                                                      (IV)

Here, $m_{\text{Plank}}$ is the mass of Plank.

Substitute equation (III) and (IV) in (II) to get $\Sigma \tau$.

  $\Sigma \tau =\left(m_{\text{child}}g\right)r_{\text{child}}+\left(m_{\text{Plank}}g\right)r_{\text{plank}}+\left(F_3\sin \theta \right)r_3$

Substitute above equation in equation (I) to get expression for $F_3$.

  $\begin{array}{c}\left(m_{\text{child}}g\right)r_{\text{child}}+\left(m_{\text{Plank}}g\right)r_{\text{plank}}+\left(F_3\sin \theta \right)r_3=0\\ F_3=\frac{\left(m_{\text{child}}g\right)r_{\text{child}}+\left(m_{\text{Plank}}g\right)r_{\text{plank}}}{F_3\sin \theta }\end{array}$            (V)

Write the equilibrium condition of the force along $x$ direction.

  $\Sigma F_x=0$                                                                                                                   (VI)

Here, $\Sigma F_x$ is the sum of all forces along $x$ direction.

Write expression for net force along $x$ direction.

  $\Sigma F_x=-F_1+F_3\cos \theta$                                                                                              (VII)

Here, $F_1$ is the magnitude of tension in rope1.

Substitute (VII) in (VI) to get $F_1$ .

  $F_1=F_3\cos \theta$                                                                                                         (VIII)

Write the equilibrium condition of the forces along $y$ direction.

  $\Sigma F_y=0$                                                                                                                  (IX)

Here, $\Sigma F_y$ is the sum of all forces along $y$ direction.

Write net forces along $y$ direction.

  $\Sigma F_y=F_2-F_{g,\text{Child}}-\left(F_{g,\text{Plank}}\right)+F_3\sin \theta$                                                                    (X)

Here, $F_2$ is the magnitude of tension in rope2.

Substitute (III) and (IV)in (X) to get $\Sigma F_y$ .

  $\Sigma F_y=F_2-m_{\text{child}}g-m_{\text{Plank}}g+F_3\sin \theta$                                                                      (XI)

Substitute (XI) in (IX) to get $F_2$ .

  $F_2=m_{\text{child}}g+m_{\text{Plank}}g-F_3\sin \theta$                                                                              (XII)

Conclusion:

Substitute $23.0\text{kg}$ for $m_{\text{Child}}$, $15.0\text{kg}$ for $m_{\text{plank}}$ , $1.00\text{m}$ for $r_{\text{child}}$, $1.25\text{m}$ for $r_{\text{plank}}$, $2.50\text{m}$ for $r_3$, $9.81\text{m}/{\text{s}}^2$ for $g$ and $35.0°$ for $\theta$ in equation (V) to get $F_3$ .

  $\begin{array}{c}{F}_3=\frac{\left(23.0\text{kg}\times 9.81\text{m}/{\text{s}}^2\right)1.00\text{m}+\left(15.0\text{kg}\times 9.81\text{m}/{\text{s}}^2\right)1.25\text{m}}{\left(2.50\right)\sin 35.0°}\\ =286\text{N}\end{array}$

Substitute $286\text{N}$ for $F_3$ and $35.0°$ for $\theta$ in equation (VIII) to get $F_1$ .

  $\begin{array}{c}{F}_1=\left(286\text{N}\right)\cos 35.0°\\ =234\text{N}\end{array}$

Substitute $23.0\text{kg}$ for $m_{\text{Child}}$, $15.0\text{kg}$ for $m_{\text{plank}}$, $286\text{N}$ for $F_3$ , $9.81\text{m}/{\text{s}}^2$ for $g$ and $35.0°$ for $\theta$ in equation (XII) to get $F_2$ .

  $\begin{array}{c}{F}_2=\left(23.0\text{kg}\times 9.81\text{m}/{\text{s}}^2\right)+\left(15.0\text{kg}\times 9.81\text{m}/{\text{s}}^2\right)-286\text{N}\sin 35.0°\\ =209\text{N}\end{array}$

Therefore, the tension in rope1 is $F_1=234\text{N}$, tension in rope2 is $F_2=209\text{N}$ and tension in rope3 is $F_3=286\text{N}$ .