Chapter 1.2, Problem 76E

(a)

To determine

To write: the volume V of the package as a function of $x$ and its domain.

Answer to Problem 76E

  $V=-4x^3+108x^2$

Domain $\in (0,27)$

Explanation of Solution

Given information:combined length and girth (perimeter of cross section) of a rectangular package is 108 inches.

Girth or perimeter of cross section of rectangular package = $4x$

Length of rectangular package = $y$

According to question,

Combined length and girth (perimeter of cross section) of a rectangular package=108

  $\begin{array}{l}\Rightarrow y+4x=108\\ \Rightarrow y=108-4x\end{array}$

Now,

Area of cross section of rectangular package = $x^2$

Length of rectangular package = $y=108-4x$

Volume of rectangular package = $x^2\times y$ = $x^2\times (108-4x)$

  $\begin{array}{l}\Rightarrow 108x^2-4x^3\\ \Rightarrow -4x^3+108x^2\end{array}$

Since $x$ can take only positive real value, then minimum value of domain =0

And Length of rectangular package should always be positive or equal to 0

  $\begin{array}{l}y\ge 0\\ \Rightarrow 108-4x\ge 0\\ \Rightarrow 4x\le 108\\ \Rightarrow x\le \frac{108}{4}=27\end{array}$

Maximum value of domain=27

Hence domain of above function belongs to $(0,27)$ .

(b)

To determine

To graph: the above found function $V=-4x^3+108x^2$ .

Explanation of Solution

Graph:

  

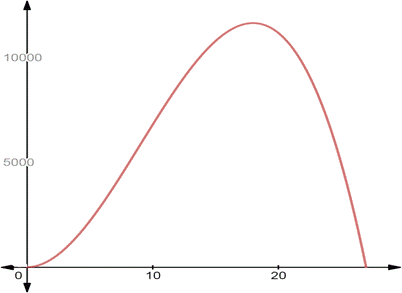
(c)

To determine

To find: the dimension that will maximize the volume of the package.

Answer to Problem 76E

  $\begin{array}{l}x=18\text{ inches}\\ \text{y=36 inches}\end{array}$

Explanation of Solution

Given information: combined length and girth (perimeter of cross section) of a rectangular package is 108 inches.

The above found equation is $V=-4x^3+108x^2$

Differentiating with respect to x, we get

  $\frac{dV}{dx}=-12x^2+216x$

Again differentiating with respect to x, we get

  $\frac{d^{2}V}{d{x}^2}=-24x+216$

Now for maximum value equate, $\frac{dV}{dx}=-12x^2+216x$ =0

  $\begin{array}{l}\Rightarrow x(-12x+216)=0\\ \Rightarrow x=0\text{ or }x=\frac{216}{12}=18\end{array}$

Now at x=18, $\frac{d^{2}V}{d{x}^2}=-24\times 18+216=-432+216=-216$< 0

Hence at x=18, V is maximum.

Putting x=18, in equation $y=108-4x$ we get

  $y=108-4(18)=108-72=36$

Thus the required dimension is,

  $\begin{array}{l}x=18\text{ inches}\\ \text{y=36 inches}\end{array}$