Chapter 11.4, Problem 44E

(a)

To determine

To find: The equation of two different ellipses with the given properties.

Answer to Problem 44E

The equation of two different ellipses with the given properties is $\frac{x^2}{3}+\frac{{\left(y-2\right)}^2}{4}=1$ and $\frac{x^2}{8}+\frac{{\left(y-3\right)}^2}{9}=1$ .

Explanation of Solution

Given information:

Conics that share a focus are called confocal. Consider the family of conics that have a focus at $\left(0,1\right)$ and vertex at origin as shown in figure below:

  

Calculation:

The focus of the ellipse lies on $y$ -axis, The general equation for ellipse is equal to $\frac{x^2}{b^2}+\frac{y^2}{a^2}=1$ .

The distance of the focus from the vertex is equal to $1$ . So, the value of $c$ is equal to $1$ .

The property $c^2=a^2-b^2$ is true in case of ellipse. So, the choice of values of $a$ and $b$ is such that $a^2-b^2=1$ .

First choice for the value of $a$ and $b$ is $2$ and $\sqrt{3}$ respectively and the second choice of $a$ and $b$ is $3$ and $2\sqrt{2}$ respectively.

Therefore, the equation of two different ellipses with the given properties are $\frac{x^2}{3}+\frac{{\left(y-2\right)}^2}{4}=1$ and $\frac{x^2}{8}+\frac{{\left(y-3\right)}^2}{9}=1$ .

(b)

To determine

To find: The equation of two different hyperbolas with the given properties.

Answer to Problem 44E

The equation of two different hyperbolas with the given properties is $\frac{{\left(y+1\right)}^2}{1}-\frac{x^2}{1}=1$ and $\frac{{\left(y+1\right)}^2}{1}-\frac{x^2}{3}=1$ .

Explanation of Solution

Given information:

Conics that share a focus are called confocal. Consider the family of conics that have a focus at $\left(0,1\right)$ and vertex at origin as shown in figure below:

  

Calculation:

The focus of the hyperbola lies on $y$ -axis, The general equation for hyperbola is equal to $\frac{{\left(y-k\right)}^2}{b^2}-\frac{{\left(x-h\right)}^2}{a^2}=1$ .

As the vertex is given as origin and the focus of the hyperbola is at $\left(0,1\right)$ . So, there are many choices of hyperbolas.

Therefore, the equation of two different hyperbolas with the given properties is $\frac{{\left(y+1\right)}^2}{1}-\frac{x^2}{1}=1$ and $\frac{{\left(y+1\right)}^2}{1}-\frac{x^2}{3}=1$ .

(c)

To determine

To find: The equation of the parabola with given properties and also the reason for unique existence of parabola.

Answer to Problem 44E

The equation of the parabola with given properties is $x^2=4y$ .

Explanation of Solution

Given information:

Conics that share a focus are called confocal. Consider the family of conics that have a focus at $\left(0,1\right)$ and vertex at origin as shown in figure below:

  

Calculation:

The focus of the parabola lies on $y$ -axis, The general equation for parabola is equal to $x^2=4fy$ .

As the vertex is given as origin and the focus of the hyperbola is at $\left(0,1\right)$ . The distance of the focus from the vertex is equal to $1$ .

Substitute $1$ for $f$ in the equation of parabola.

  $\begin{array}{c}{x}^2=4fy\\ x^2=4\left(1\right)y\\ x^2=4y\end{array}$

The value of $f$ is unique. So, the equation of the parabola is also unique for the given conditions.

So, there exist only one parabola for the given conditions.

Therefore, the equation of the parabola with given properties is $x^2=4y$ .

(d)

To determine

To graph: The conics found in part(a), (b) and (c) on the same coordinate axis.

Explanation of Solution

Given information:

Conics that share a focus are called confocal. Consider the family of conics that have a focus at $\left(0,1\right)$ and vertex at origin as shown in figure below:

  

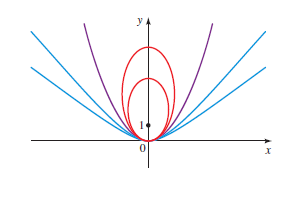
Graph:

The graph of the conics found in part(a), (b) and (c) are shown in the figure below:

  

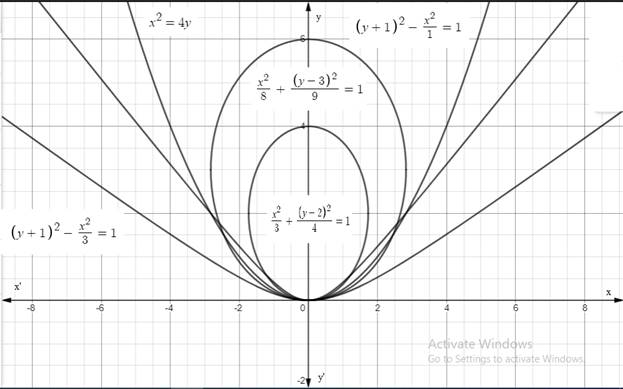
Figure(1)

(e)

To determine

To find: How the ellipses and hyperbolas are related to parabola.

Answer to Problem 44E

All the ellipses, parabolas and hyperbolas have the same vertex and same focus and also the parabola can be transformed in to the ellipses and hyperbolas with some transformations in equation.

Explanation of Solution

Given information:

Conics that share a focus are called confocal. Consider the family of conics that have a focus at $\left(0,1\right)$ and vertex at origin as shown in figure below:

  

Calculation:

All the ellipses, parabolas and hyperbolas have the same vertex and same focus.

The parabola can be transformed in to the ellipses and hyperbolas with some transformations in equation.

Therefore, the ellipses and hyperbolas are related to parabola with focus and vertex.