
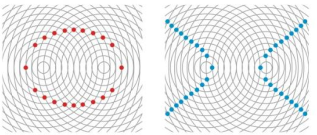
Ripples in Pool Two stones are dropped simultaneously into a calm pool of water. The crests of the resulting waves form equally spaced concentric circles, as shown in the figures.
The waves interact with each other to create certain interference patterns.
- (a) Explain why the red dots lie on an ellipse.
- (b) Explain why the blue dots lie on a hyperbola.
(a)
To explain: The reason for the red dots lie on an ellipse
Answer to Problem 50E
Because of for any red dot the sum of the distance from the two-fixed point remain same.
Explanation of Solution
Definition used:
Geometric definition of ellipse:
“An ellipse is the set of all points in the plane, the sum of whose distance from two fixed points
Description:
Given that two stone are dropped simultaneously into a calm pool of water.
The crests of the resulting wave form equally spaced concentric circles.
The center of the circles is fixed, say
For any red dot, the sum of the number of crests from
Therefore, for any red dot the sum of the distance from the two-fixed point remain same. Hence, by geometric definition of the ellipse stated above, conclude that, the red dots are on an ellipse with foci as
(b)
To explain: The reason for the blue dots lie on a hyperbola.
Answer to Problem 50E
Because of for any red dot the differences of the distance from the two-fixed point remain same.
Explanation of Solution
Definition used:
Geometric definition of hyperbola:
“A hyperbola is the set of all points in the plane, the difference of whose distances from two fixed points
Description:
Given that two stone are dropped simultaneously into a calm pool of water.
The crests of the resulting wave form equally spaced concentric circles.
The center of the circles is fixed, say
For any blue dot, the difference of the number of crests from
Therefore, for any blue dot the difference of the distance from the two-fixed point remain same. Hence, by geometric definition of the hyperbola stated above, conclude that, the red dots are on an ellipse with foci as
Chapter 11 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





