Physics (5th Edition)
5th Edition
ISBN: 9780321976444
Author: James S. Walker
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 11, Problem 34PCE
A stick with a mass of 0.214 kg and a length of 0.436 m rests in contact with a bowling ball and a rough floor, as shown in Figure 11-48. The bowling ball has a diameter of 21.6 cm, and the angle the stick makes with the horizontal is 30.0°. You may assume there is no friction between the stick and the bowling ball, though friction with the floor must be taken into account. (a) Find the magnitude of the force exerted on the stick by the bowling ball. (b) Find the horizontal component of the force exerted on the stick by the floor. (c) Repeat part (b) for the vertical component of the force.
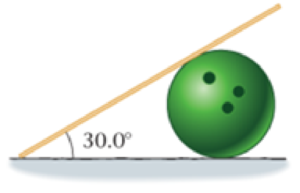
Figure 11-48 Problem 34
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A 10 N ball is supported by an incline and a cable making an angle a with the
vertical direction. Knowing the force in the cable equal to 5 N, determine the
angle a and the force exerted by the ball on the incline. Consider the ball as a
particle.
As shown in the figure below, a stick of length L = 0.435 m and mass m = 0.300 kg is in contact with a rough floor at one end and a frictionless bowling ball (diameter d = 15.00 cm) at some other point such that the angle between the stick and the floor is e = 30°.
Determine the following.
30.0°
(a) magnitude of the force exerted on the stick by the bowling ball
1.49
Since the stick is in static equilibrium, we expect to use the first and second condition of equilibrium. Since we need to determine torques, before starting the problem, see if you can write an expression for the torque in terms of the force producing the torque
and the perpendicular distance between the line of action of this force and the point about which we are determining the torques. Determine a convenient point about which to determine the torques. It will be to your advantage to draw a careful figure which
includes the stick, all dimensions and angles, all forces acting on the stick, the point about which you plan…
A 2×12 board is about 2.18 kg per linear foot. A 16-foot length board of Southern Yellow Pine is placed against a wall such that the angle between the wall and the length of the board is 20°. Assume that the wall is perfectly smooth (a.k.a. the coefficient of friction between the wall and the board is zero). (a) What is the normal force between the wall and the board? (b) What is the normal force between the board and the floor? (c) What is the force of static friction between the board and the floor? (d) What is the coefficient of static friction between the board and the floor?
Chapter 11 Solutions
Physics (5th Edition)
Ch. 11.1 - A bicycle wheel is mounted on an axle, as shown in...Ch. 11.2 - Consider two objects with the following...Ch. 11.3 - A Physics sign is supported symmetrically by two...Ch. 11.4 - A mobile made from three piggy banks (A, B, C) is...Ch. 11.5 - Prob. 5EYUCh. 11.6 - Consider two objects with the following...Ch. 11.7 - Prob. 7EYUCh. 11.8 - In system 1, a torque of 20 N m acts through an...Ch. 11.9 - The angular velocity of the spinning bicycle wheel...Ch. 11 - Two forces produce the same torque. Does it follow...
Ch. 11 - A car pitches down in front when the brakes are...Ch. 11 - A tightrope walker uses a long pole to aid in...Ch. 11 - When a motorcycle accelerates rapidly from a stop...Ch. 11 - Give an example of a system in which the net...Ch. 11 - Give an example of a system in which the net force...Ch. 11 - Is the normal force exerted by the ground the same...Ch. 11 - Give two everyday examples of objects that are not...Ch. 11 - Give two everyday examples of objects that are in...Ch. 11 - Can an object have zero translational acceleration...Ch. 11 - Stars form when a large rotating cloud of gas...Ch. 11 - What purpose does the tail rotor on a helicopter...Ch. 11 - Is it possible to change the angular momentum of...Ch. 11 - Suppose a diver springs into the air with no...Ch. 11 - To tighten a spark plug, it is recommended that a...Ch. 11 - Pulling a Weed The gardening tool shown in Figure...Ch. 11 - A person slowly lowers a 3.6-kg crab trap over the...Ch. 11 - A squirrel-proof bird feeder has a lever that...Ch. 11 - At one position during its cycle, the foot pushes...Ch. 11 - BIO Predict/Calculate Force to Hold a Baseball A...Ch. 11 - At the local playground, a 21-kg child sits on the...Ch. 11 - Predict/Explain Consider the pulley-block systems...Ch. 11 - Suppose a torque rotates your body about one of...Ch. 11 - A torque of 0.97 N m is applied to a bicycle...Ch. 11 - When a ceiling fan rotating with an angular speed...Ch. 11 - When the play button is pressed, a CD accelerates...Ch. 11 - A person holds a ladder horizontally at its...Ch. 11 - A 0.180-kg wooden rod is 1.25 m long and pivots at...Ch. 11 - Predict/Calculate A wheel on a game show is given...Ch. 11 - The L-shaped object in Figure 11-41 consists of...Ch. 11 - The L-shaped object described in the previous...Ch. 11 - A motorcycle accelerates from rest, and both the...Ch. 11 - Predict/Calculate A torque of 13 N m is applied...Ch. 11 - Predict/Explain Suppose the person in Example...Ch. 11 - A string that passes over a pulley has a 0.321-kg...Ch. 11 - To loosen the lid on a jar of jam 7.6 cm in...Ch. 11 - BIO Predict/Calculate Referring to the person...Ch. 11 - Prob. 24PCECh. 11 - Prob. 25PCECh. 11 - Predict/Calculate A schoolyard teeter-totter with...Ch. 11 - A 0.122-kg remote control 23.0 cm long rests on a...Ch. 11 - Predict/Calculate A 0.16-kg meterstick is held...Ch. 11 - Prob. 29PCECh. 11 - A uniform metal rod, with a mass of 2.0 kg and a...Ch. 11 - Prob. 31PCECh. 11 - In Figure 11-46 two acrobats perform a balancing...Ch. 11 - BIO Forces in the Foot In Figure 11-47 we see the...Ch. 11 - A stick with a mass of 0.214 kg and a length of...Ch. 11 - Prob. 35PCECh. 11 - If the cat in Example 11-9 has a mass of 3.9 kg,...Ch. 11 - Prob. 37PCECh. 11 - Maximum Overhang Three identical, uniform books of...Ch. 11 - A baseball bat balances 71.1 cm from one end. If a...Ch. 11 - A 2.85-kg bucket is attached to a rope wrapped...Ch. 11 - A child exerts a tangential 53 4-N force on the...Ch. 11 - Predict/Calculate You pull downward with a force...Ch. 11 - One elevator arrangement includes the passenger...Ch. 11 - Atwood's Machine An Atwoods machine consists of...Ch. 11 - A 1.4-kg bicycle tire with a radius of 33 cm...Ch. 11 - Jogger 1 in Figure 11-51 has a mass of 65.3 kg and...Ch. 11 - Predict/Calculate Suppose jogger 3 in Figure 11-51...Ch. 11 - A torque of 0.12 N m is applied to an egg beater...Ch. 11 - A windmill has an initial angular momentum of 8500...Ch. 11 - Two gerbils run in place with a linear speed of...Ch. 11 - Predict/Explain A student rotates on a...Ch. 11 - A puck on a horizontal, frictionless surface is...Ch. 11 - A puck on a horizontal, frictionless surface is...Ch. 11 - As an ice skater begins a spin, his angular speed...Ch. 11 - A disk-shaped merry-go-round of radius 2.63 m and...Ch. 11 - A student sits at rest on a piano stool that can...Ch. 11 - Predict/Calculate A turntable with a moment of...Ch. 11 - A student on a piano stool rotates freely with an...Ch. 11 - Walking on a Merry-Go-Round A child of mass m...Ch. 11 - Predict/Explain Two spheres of equal mass and...Ch. 11 - Turning a doorknob through 0.25 of a revolution...Ch. 11 - A person exerts a tangential force of 36.1 N on...Ch. 11 - To prepare homemade ice cream a crank must be...Ch. 11 - Power of a Dental Drill A popular make of dental...Ch. 11 - For a home repair job you must turn the handle of...Ch. 11 - The L-shaped object in Figure 11-40 consists of...Ch. 11 - The rectangular object in Figure 11-41 consists of...Ch. 11 - Predict/Calculate A circular saw blade accelerates...Ch. 11 - CE A uniform disk stands upright on its edge, and...Ch. 11 - CE Consider the two rotating systems shown in...Ch. 11 - CE Predict/Explain A disk and a hoop (bicycle...Ch. 11 - CE A beetle sits at the nm of a turntable that is...Ch. 11 - After getting a drink of water a hamster jumps...Ch. 11 - A 47.0-kg uniform rod 4.25 m long is attached to a...Ch. 11 - Prob. 75GPCh. 11 - BIO The Masseter Muscle The masseter muscle, the...Ch. 11 - Exercising the Biceps You are designing exercise...Ch. 11 - Prob. 78GPCh. 11 - In Example 11-11, suppose the ladder is uniform,...Ch. 11 - When you arrive at Dukes Dude Ranch you are...Ch. 11 - Prob. 81GPCh. 11 - Flats Versus Heels A woman might wear a pair of...Ch. 11 - BIO A young girl sits at the edge of a dock by the...Ch. 11 - BIO Deltoid Muscle A crossing guard holds a STOP...Ch. 11 - BIO Triceps To determine the force a persons...Ch. 11 - Predict/Calculate Suppose partial melting of the...Ch. 11 - A bicycle wheel of radius R and mass M is at rest...Ch. 11 - A 0.101-kg yo-yo has an outer radius R that is...Ch. 11 - BIO Peak Pedaling Torque The downward force...Ch. 11 - A cylinder of mass m and radius r has a string...Ch. 11 - Bricks in Equilibrium Consider a system of four...Ch. 11 - BIO Correcting Torsiversion Torsiversion is a...Ch. 11 - BIO Correcting Torsiversion Torsiversion is a...Ch. 11 - BIO Correcting Torsiversion Torsiversion is a...Ch. 11 - BIO Correcting Torsiversion Torsiversion is a...Ch. 11 - Referring to Example 11-14 Suppose the mass of the...Ch. 11 - Prob. 97PPCh. 11 - Referring to Quick Example 11-22 Suppose the child...Ch. 11 - Referring to Quick Example 11-22 Suppose...
Additional Science Textbook Solutions
Find more solutions based on key concepts
TEST YOUR UNDERSTANDING OF SECTION 23.2 If the electric potential at a certain point is zero, does the electric...
University Physics with Modern Physics (14th Edition)
5. The following passages and associated questions are based on the material of Part II.
Big Air
A new generati...
College Physics: A Strategic Approach (3rd Edition)
Choose the best answer to etch of the following. Explain your reasoning. 12.Natural selection is done name give...
The Cosmic Perspective Fundamentals (2nd Edition)
To simulate the apparent weightlessness of space orbit, astronauts are trained in the hold of a cargo aircraft ...
College Physics
Description of Motion:
Tutorials in Introductory Physics
Write the SI unit for each abbreviation.
28. 125 kg
Applied Physics (11th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- In the figure, a climber leans out against a vertical ice wall that has negligible friction. Distance a is 0.975 m and distance L is 1.90 m. His center of mass is distance d = 0.91 m from the feet-ground contact point. If he is on the verge of sliding, what is the coefficient of static friction between feet and ground?arrow_forwardA uniform board is leaning against a smooth vertical wall. The board is at an angle above the horizontal ground. The coefficient of static friction between the ground and the lower end of the board is 0.890. Find the smallest value for the angle , such that the lower end of the board does not slide along the ground.arrow_forwardA uniform board is leaning against a smooth vertical wall. The board is at an angle θ above the horizontal ground. The coefficient of static friction between the ground and the lower end of the board is 0.650. Find the smallest value for the angle θ, such that the lower end of the board does not slide along the ground.arrow_forward
- In the figure a 50 kg rock climber is in a lie-back climb along a fissure, with hands pulling on one side of the fissure and feet pressed against the opposite side. The fissure has width w = 0.20 m, and the center of mass of the climber is a horizontal distance d = 0.45 m from the fissure. The coefficient of static friction between hands and rock is μ1 = 0.50, and between boots and rock it is μ2 = 1.15. The climber adjusts the vertical distance h between hands and feet until the (identical) pull by the hands and push by the feet is the least that keeps him from slipping down the fissure. (He is on the verge of sliding.) (a) What is the least horizontal pull by the hands and push by the feet that will keep the climber stable? (b) What is the value of h?arrow_forwardIn the figure a 51 kg rock climber is in a lie-back climb along a fissure, with hands pulling on one side of the fissure and feet pressed against the opposite side. The fissure has width w = 0.30 m, and the center of mass of the climber is a horizontal distance d = 0.30 m from the fissure. The coefficient of static friction between hands and rock is µ₁ = 0.40, and between boots and rock it is µ2 = 1.10. The climber adjusts the vertical distance h between hands and feet until the (identical) pull by the hands and push by the feet is the least that keeps him from slipping down the fissure. (He is on the verge of sliding.) (a) What is the least horizontal pull by the hands and push by the feet that will keep the climber stable? (b) What is the value of h? (a) Number Units (b) Number Units comarrow_forwardAn 85 kg window cleaner uses a 10 kg ladder that is 5.3 m long. He places one end on the ground 3.2 m from a wall, rests the upper end against a cracked window, and climbs the ladder. He is 1.6 m up along the ladder when the window breaks. Neglect friction between the ladder and window and assume that the base of the ladder does not slip. When the window is on the verge of breaking, what are (a) the magnitude of the force on the window from the ladder, (b) the magnitude of the force on the ladder from the ground, and (c) the angle (relative to the horizontal) of that force on the ladder?arrow_forward
- In the figure a 60 kg rock climber is in a lie-back climb along a fissure, with hands pulling on one side of the fissure and feet pressed against the opposite side. The fissure has width w = 0.30 m, and the center of mass of the climber is a horizontal distance d = 0.20 m from the fissure. The coefficient of static friction between hands and rock is μ₁ = 0.30, and between boots and rock it is μ2 = 1.10. The climber adjusts the vertical distance h between hands and feet until the (identical) pull by the hands and push by the feet is the least that keeps him from slipping down the fissure. (He is on the verge of sliding.) (a) What is the least horizontal pull by the hands and push by the feet that will keep the climber stable? (b) What is the value of h? <311 h com (a) Number i Units = (b) Number i Units =arrow_forwardA ladder, whose length 10 m and whose mass is 40 kg rest against a frictionless vertical wall. Its upperend is a distance of 7.7 m above the ground. The center of mass of the ladder is 1/3 of the way up the ladder. The coefficient of static friction between the ladder and the ground is 0.53. If a carpenter climbs 85% of the way up the ladder before it starts to slip, find the mass of the carpenter.arrow_forwardIn the figure, a lead brick rests horizontally on cylinders A and B. The areas of the top faces of the cylinders are related by A- 2.4 Ag: the Young's moduli of the cylinders are related by EA- 2.1 Eg. The cylinders had identical lengths before the brick was placed on them. What fraction of the brick's mass is supported (a) by cylinder A and (b) by cylinder B? The horizontal distances between the center of mass of the brick and the centerlines of the cylinders are dafor cylinder A and dg for cylinder B. (c) What is the ratio da/dg? com of brick (a) Number i Units (b) Number Units (c) Number Unitsarrow_forward
- A crate, in the form of a cube with edge lengths of 1.2 m, contains a piece of machinery; the center of mass of the crate and its contents is located 0.30 m above the crate’s geometrical center.The crate rests on a ramp that makes an angle u with the horizontal.As u is increased from zero, an angle will be reached at which the crate will either tip over or start to slide down the ramp. If the coefficient of static friction ms between ramp and crate is 0.60, (a) does the crate tip or slide and (b) at what angle u does this occur? If ms = 0.70, (c) does the crate tip or slide and (d) at what angle u does this occur? (Hint: At the onset of tipping, where is the normal force located?)arrow_forwardYou cross a horizontal rigid bridge of uniform density and length L. The bridge weighs 3671 and is resting on two concrete pillars, one at each end. You cross 1/5 of the length of the bridge and stop. If your weight is 1030.22 N, what is the magnitude (no sign) of the force that the first concrete pillar exerts on the bridge? That pillar is 1/5 of the length away from you, back where you started to cross.arrow_forwardA beam with a length of 2 m and a mass of 10 kg supports a 50 kg box. The beam is connected to a wall by a hinge at its base and a horizontal wire. The wire is connected to the beam 1.5 m from the hinge and makes an angle θ of 35o to the beam. The goal is to find the tension in the wire and the horizontal and vertical components of the force exerted by the hinge on the boardarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Static Equilibrium: concept; Author: Jennifer Cash;https://www.youtube.com/watch?v=0BIgFKVnlBU;License: Standard YouTube License, CC-BY