
Concept explainers
BIO Correcting Torsiversion
Torsiversion is a medical condition in which a tooth is rotated away from its normal position about the long axis of the root Studies show that about 2 percent of the population suffer from this condition to some degree. For those who do, the improper alignment of the tooth can lead to tooth-to-tooth collisions during eating, as well as other problems. Typical patients display a rotation ranging from 20° to 60°, with an average around 30°.
An example is shown in Figure 11-69 (a), where the first premolar is not only displaced slightly from its proper location in the negative y direction, but also rotated clockwise from its normal orientation. To correct this condition an orthodontist might use an archwire and a bracket to apply both a force and a torque to the tooth. In the simplest case, two forces are applied to the tooth in different locations, as indicated by F1 and F2 in Figure 11-69 (a). These two forces, if chosen properly, can reposition the tooth by exerting a net force in the positive y direction, and also reorient it by applying a torque in the counterclockwise direction.
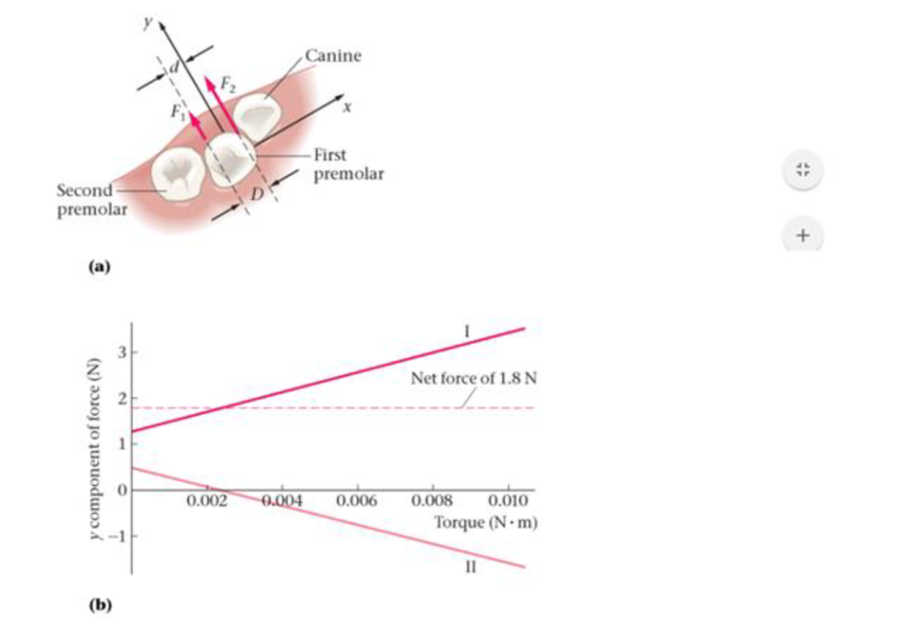
Figure 11-69 Problems 92, 93, 94, and 95
In a typical case it may be desired to have a net force in the positive y direction of 1.8 N. In addition, the distances in Figure 11-69 (a) can be taken to be d = 3.2 mm and D = 4.5 mm. Given these conditions, a range of torques is possible for various values of the y components of the forces, F1y and F2y. For example Figure 11-69 (b) shows the values of F1y and F2y necessary to produce a given torque, where the torque is measured about the center of the tooth (which is also the origin of the coordinate system). Notice that the two forces always add to 1.8 N in the positive y direction, though one of the forces changes sign as the torque is increased.
95. •• Find the values of F1y and F2y required to give zero net torque of 0.0099 N · m. This is a torque that would be effective at rotating the tooth.
- A. F1y = −1.7 N, F2y = 3.5 N
- B. F1y = −3.8 N, F2y = 5.6 N
- C. F1y = −0.23 N, F2y = 2.0 N
- D. F1y = −4.0 N, F2y = −2.2N
Want to see the full answer?
Check out a sample textbook solution
Chapter 11 Solutions
Physics (5th Edition)
Additional Science Textbook Solutions
Microbiology: An Introduction
Chemistry: A Molecular Approach (4th Edition)
Anatomy & Physiology (6th Edition)
Genetic Analysis: An Integrated Approach (3rd Edition)
Human Biology: Concepts and Current Issues (8th Edition)
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
- PROBLEM 2 A cube of mass m is placed in a rotating funnel. (The funnel is rotating around the vertical axis shown in the diagram.) There is no friction between the cube and the funnel but the funnel is rotating at just the right speed needed to keep the cube rotating with the funnel. The cube travels in a circular path of radius r, and the angle between the vertical and the wall of the funnel is 0. Express your answers to parts (b) and (c) in terms of m, r, g, and/or 0. (a) Sketch a free-body diagram for the cube. Show all the forces acting on it, and show the appropriate coordinate system to use for this problem. (b) What is the normal force acting on the cube? FN=mg58 (c) What is the speed v of the cube? (d) If the speed of the cube is different from what you determined in part (c), a force of friction is necessary to keep the cube from slipping in the funnel. If the funnel is rotating slower than it was above, draw a new free-body diagram for the cube to show which way friction…arrow_forwardCircular turns of radius r in a race track are often banked at an angle θ to allow the cars to achieve higher speeds around the turns. Assume friction is not present. Write an expression for the tan(θ) of a car going around the banked turn in terms of the car's speed v, the radius of the turn r, and g so that the car will not move up or down the incline of the turn. tan(θ) =arrow_forwardThe character Min Min from Arms was a DLC character added to Super Smash Bros. Min Min’s arms are large springs, with a spring constant of 8.53 ⋅ 10^3 N/m, which she uses to punch and fling away her opponents. Min Min pushes her spring arm against Steve, who is not moving, compressing it 1.20 m as shown in figure A. Steve has a mass of 81.6 kg. Assuming she uses only the spring to launch Steve, how fast is Steve moving when the spring is no longer compressed? As Steve goes flying away he goes over the edge of the level, as shown in figure C. What is the magnitude of Steve’s velocity when he is 2.00 m below where he started?arrow_forward
- Slinky dog whose middle section is a giant spring with a spring constant of 10.9 N/m. Woody, who has a mass of 0.412 kg, grabs onto the tail end of Slink and steps off the bed with no initial velocity and reaches the floor right as his velocity hits zero again. How high is the bed? What is Woody’s velocity halfway down? Enter just the magnitude of velocity.arrow_forwardNo chatgpt pls will upvotearrow_forwardA positive charge of 91 is located 5.11 m to the left of a negative charge 92. The charges have different magnitudes. On the line through the charges, the net electric field is zero at a spot 2.90 m to the right of the negative charge. On this line there are also two spots where the potential is zero. (a) How far to the left of the negative charge is one spot? (b) How far to the right of the negative charge is the other?arrow_forward
- A charge of -3.99 μC is fixed in place. From a horizontal distance of 0.0423 m, a particle of mass 7.31 x 103 kg and charge -9.76 µC is fired with an initial speed of 84.1 m/s directly toward the fixed charge. How far does the particle travel before its speed is zero?arrow_forwarda) What is the minimum tension in N that the cable must be able to support without breaking? Assume the cable is massless. T = b) If the cable can only support a tension of 10,000 N what is the highest mass the ball can have in kg? mm =arrow_forwardCurve Fitter CURVE FITTER Open Update Fit Save New Exclusion Rules Select Validation Data Polynomial Exponential Logarithmic Auto Fourier Fit Fit Duplicate Data Manual FILE DATA FIT TYPE FIT Harmonic Motion X us 0.45 mi ce 0.4 0.35 0.3 0.25 0.2 Residuals Plot Contour Plot Plot Prediction Bounds None VISUALIZATION Colormap Export PREFERENCES EXPORT Fit Options COA Fourier Equation Fit Plot x vs. t -Harmonic Motion a0+ a1*cos(x*w) + b1*sin(x*w) Number of terms Center and scale 1 ▸ Advanced Options Read about fit options Results Value Lower Upper 0.15 a0 0.1586 0.1551 0.1620 a1 0.0163 0.0115 0.0211 0.1 b1 0.0011 -0.0093 0.0115 W 1.0473 0.9880 1.1066 2 8 10 t 12 14 16 18 20 Goodness of Fit Value Table of Fits SSE 0.2671 Fit State Fit name Data Harmonic Motion x vs. t Fit type fourier1 R-square 0.13345 SSE DFE 0.26712 296 Adj R-sq 0.12467 RMSE 0.030041 # Coeff Valic R-square 0.1335 4 DFE 296.0000 Adj R-sq 0.1247 RMSE 0.0300arrow_forward
- What point on the spring or different masses should be the place to measure the displacement of the spring? For instance, should you measure to the bottom of the hanging masses?arrow_forwardLet's assume that the brightness of a field-emission electron gun is given by β = 4iB π² d²α² a) Assuming a gun brightness of 5x108 A/(cm²sr), if we want to have an electron beam with a semi-convergence angle of 5 milliradian and a probe current of 1 nA, What will be the effective source size? (5 points) b) For the same electron gun, plot the dependence of the probe current on the parameter (dpa) for α = 2, 5, and 10 milliradian, respectively. Hint: use nm as the unit for the electron probe size and display the three plots on the same graph. (10 points)arrow_forwardi need step by step clear answers with the free body diagram clearlyarrow_forward
 College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





