College Physics (10th Edition)
10th Edition
ISBN: 9780321902788
Author: Hugh D. Young, Philip W. Adams, Raymond Joseph Chastain
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 10, Problem 49P
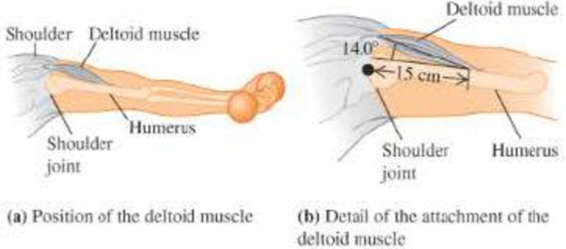
The deltoid muscle. The deltoid muscle is the main muscle that allows you to raise your arm or even hold it out. It is connected to the humerus of the upper arm. (See Figure 10.66a.) The person shown is holding his arm out horizontally with a 2.50 kg weight in his hand. This weight is 60.0 cm from the shoulder joint. His forearm (including his hand) has a mass of 2.44 kg and is 34.0 cm long; its center of mass is 43 cm from the shoulder joint, measured along the arm. His upper arm is 26.0 cm long and has a mass of 2.63 kg; its center of mass is 13.0 cm from the shoulder joint. The deltoid muscle is attached to the humerus 15.0 cm from the shoulder joint and makes a 14.0° angle with the humerus. (See Figure 10.66b.) (a) Make a free-body diagram of the arm. (b) What is the tension in the deltoid muscle?
Figure 10.66
Problem 49.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Cole is trying a biceps curl and attempting to lift a 150 N dumbbell. The moment arm of this weight about his elbow joint is 25 cm. The force created by the elbow flexor muscles is 2000 N. The moment arm of the elbow flexor muscles is 2 cm. Is Cole able to lift the weight with this amount of force in his flexor muscles?
A person places his hand palm downward on a scale and pushes down on the scale until it reads (8.31x10^1) N. The triceps muscle is responsible for this arm extension force. Find the force (in N) exerted by the triceps muscle. The bottom of the triceps muscle is 2.50 cm to the left of the elbow joint, and the palm is pushing at approximately 35.0 cm to the right of the elbow joint. (please ignore the number 96 shown in the scale). Give your answer with three significant figures.
Bugs Bunny, during his training for the Space Jam sequel, is trying to perform a biceps curl and is attempting to lift a 150 N dumbbell. The moment arm of this weight about his elbow joint is 25 cm. The force created by the elbow flexor muscles is 2000 N. The moment arm of the elbow flexor muscles is 2 cm. Is Bugs able to lift the weight with this amount of force in his flexor muscles?
Chapter 10 Solutions
College Physics (10th Edition)
Ch. 10 - When tightening a bolt, mechanics sometimes extend...Ch. 10 - Prob. 2CQCh. 10 - Two identical uniform 30 cm bricks are placed one...Ch. 10 - (a) If the forces on an object balance, do the...Ch. 10 - (a) Can you change the location of your bodys...Ch. 10 - Serious bicyclists say that if you reduce the...Ch. 10 - Prob. 7CQCh. 10 - In terms of torques, discuss the action of a claw...Ch. 10 - Why is a tapered water glass with a narrow base...Ch. 10 - True or false? In picking an axis about which to...
Ch. 10 - Global warming. As the earths climate continues to...Ch. 10 - If two spinning objects have the same angular...Ch. 10 - You are designing a wheel that must have a fixed...Ch. 10 - Prob. 2MCPCh. 10 - A student is sitting on a frictionless rotating...Ch. 10 - If the torques on an object balance, then it...Ch. 10 - If the forces on an object balance, then it...Ch. 10 - Prob. 6MCPCh. 10 - A person pushes vertically downward with force P...Ch. 10 - String is wrapped around the outer rim of a solid...Ch. 10 - A ball of mass 0.20 kg is whirled in a horizontal...Ch. 10 - A heavy solid disk rotating freely and slowed only...Ch. 10 - A uniform metal meterstick is balanced as shown in...Ch. 10 - Prob. 1PCh. 10 - Calculate the net torque about point O for the two...Ch. 10 - Three forces are applied to a wheel of radius...Ch. 10 - A 4 N and a 10 N force act on an object. The...Ch. 10 - A square metal plate 0.180 m on each side is...Ch. 10 - A cord is wrapped around the rim of a wheel 0.250...Ch. 10 - A certain type of propeller blade can be modeled...Ch. 10 - A 750 g grinding wheel 25.0 cm in diameter is in...Ch. 10 - A grindstone in the shape of a solid disk with...Ch. 10 - A solid, uniform cylinder with mass 8.00 kg and...Ch. 10 - A 2.00 kg stone is tied to a thin, light wire...Ch. 10 - A light rope is wrapped several times around a...Ch. 10 - A thin, light string is wrapped around the rim of...Ch. 10 - 14. A uniform, 8.40-kg, spherical shell 50.0 cm in...Ch. 10 - A hollow spherical shell with mass 2.00 kg rolls...Ch. 10 - A solid disk of radius 8.50 cm and mass 1.25 kg,...Ch. 10 - What is the power output in horsepower of an...Ch. 10 - A solid uniform sphere of mass 5 kg and radius 0.1...Ch. 10 - A playground merry-go-round has a radius of 4.40 m...Ch. 10 - The flywheel of a motor has a mass of 300.0 kg and...Ch. 10 - Calculate the angular momentum and kinetic energy...Ch. 10 - (a) Calculate the magnitude of the angular...Ch. 10 - A small 0.300 kg bird is flying horizontally at...Ch. 10 - A. small 4.0 kg brick is released from rest 2.5 m...Ch. 10 - The London Eye is the tallest Ferris wheel in...Ch. 10 - A certain drawbridge can be modeled as a uniform...Ch. 10 - On an old-fashioned rotating piano stool, a woman...Ch. 10 - The spinning figure skater. The outstretched hands...Ch. 10 - A small block on a frictionless horizontal surface...Ch. 10 - A uniform 2 kg solid disk of radius R 0.4 m is...Ch. 10 - A diver comes off a board with arms straight up...Ch. 10 - A large turntable rotates about a fixed vertical...Ch. 10 - A large wooden turntable in the shape of a flat...Ch. 10 - Which of the objects shown in Figure 10.55 are in...Ch. 10 - (a) In each of the objects in Figure 10.56, what...Ch. 10 - Prob. 36PCh. 10 - Prob. 37PCh. 10 - Prob. 38PCh. 10 - Prob. 39PCh. 10 - Prob. 40PCh. 10 - The horizontal beam in Figure 10.60 weighs 150 N,...Ch. 10 - The boom in Figure 10.61 weighs 2600 N and is...Ch. 10 - A uniform ladder 7.0 m long weighing 450 N rests...Ch. 10 - A 9.0 m uniform beam is hinged to a vertical wall...Ch. 10 - A uniform beam 4.0 m long and weighing 2500 N...Ch. 10 - A diving board 3.00 m long is supported at a point...Ch. 10 - Two people carry a heavy electric motor by placing...Ch. 10 - Pumping iron. A 72.0 kg weightlifter is doing arm...Ch. 10 - The deltoid muscle. The deltoid muscle is the main...Ch. 10 - The rotor (flywheel) of a toy gyroscope has a mass...Ch. 10 - For each of the following rotating objects,...Ch. 10 - Prob. 52GPCh. 10 - A good workout. You are doing exercises on a...Ch. 10 - Prior to being placed in its hole, a 5700 N,...Ch. 10 - Prob. 55GPCh. 10 - One end of a 1.2-m-long beam is hinged to a...Ch. 10 - The farmyard gate. A gate 4.00 m wide and 2.00 m...Ch. 10 - 58. Atwoods machine. Figure 10.72 illustrates an...Ch. 10 - Prob. 59GPCh. 10 - The forces on the foot. A 750 N athlete standing...Ch. 10 - A uniform solid cylinder of mass M is supported on...Ch. 10 - Prob. 62GPCh. 10 - You are trying to raise a bicycle wheel of mass m...Ch. 10 - An experimental bicycle wheel is placed on a test...Ch. 10 - Prob. 65GPCh. 10 - Disks A and B are mounted on shaft SS and may be...Ch. 10 - One end of a thin, uniform rod is connected to a...Ch. 10 - A uniform, 7.5-m-long beam weighing 9000 N is...Ch. 10 - Human moment of inertia. The moment of inertia of...Ch. 10 - While the turntable is being accelerated, the...Ch. 10 - A doubling of the torque produces a greater...Ch. 10 - If the bodys center of mass were not placed on the...Ch. 10 - Torques and tug-of-war. In a study of the...Ch. 10 - If the competitor leans slightly farther back...Ch. 10 - Torques and tug-of-war. In a study of the...
Additional Science Textbook Solutions
Find more solutions based on key concepts
WHAT IF? In 2005, at least ten grizzly bears in the greater Yellowstone ecosystem were killed through contact w...
Campbell Biology in Focus (2nd Edition)
27. Consider the reaction.
Express the rate of the reaction in terms of the change in concentration of each of...
Chemistry: Structure and Properties (2nd Edition)
Flask A contains yeast cells in glucose-minimal salts broth incubated at 30C with aeration. Flask B contains ye...
Microbiology: An Introduction
Modified True/False 6. __________ Halophiles inhabit extremely saline habitats, such as the Great Salt Lake.
Microbiology with Diseases by Body System (5th Edition)
All of the following terms can appropriately describe humans except: a. primary consumer b. autotroph c. hetero...
Human Biology: Concepts and Current Issues (8th Edition)
Where are skeletal cartilages located?
Human Anatomy & Physiology (2nd Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A person places his hand palm downward on a scale and pushes down on the scale until it reads 96.0 N. The triceps muscle is responsible for this arm extension force. Find the force exerted by the triceps muscle. The bottom of the triceps muscle is 2.50 cm to the left of the elbow joint, and the palm is pushing at approximately 29.0 cm to the right of the elbow joint. P 96.0 N 2.50 cm and Q = 29.0 cm. where P =arrow_forwardWhen a gymnast weighing 740 N executes the iron cross as in figure (a), the primary muscles involved in supporting this position are the latissimus dorsi ("lats") and the pectoralis major ("pecs"). The rings exert an upward force on the arms and support the weight of the gymnast. The force exerted by the shoulder joint on the arm is labeled Fs while the two muscles exert a total force Fm on the arm. Determine the magnitude of the force Fm. Note that one ring supports half the weight of the gymnast, which is w = 370 N as indicated in figure (b). Assume that the force Fm acts at an angle of 45° below the horizontal at a distance of 4.0 cm from the shoulder joint. In your estimate, take the distance from the shoulder joint to the hand to be L = 71 cm and ignore the weight of the arm.arrow_forwardThe bones of the forearm (radius and ulna) are hinged to the humerus at the elbow. The biceps muscle connects to the bones of the forearm about 2.15 cm beyond the joint. Assume the forearm has a mass 2.25 kg and a length of 0.425 m. When the humerus and the biceps are nearly vertical and the forearm is horizontal, if a person wishes to hold an object of mass 7.35 kg so that her forearm remains motionless, what is the force F exerted by the biceps muscle? Image is attached below. Please show all work.arrow_forward
- The large quadriceps muscle in the upper leg terminates at its lower end in a tendon attached to the upper end of the tibia (see Figure a). The forces on the lower leg when the leg is extended are modeled as in Figure b, where T is the force of tension in the tendon, w is the force of gravity acting on the lower leg, and F is the force of gravity acting on the foot. Find T when the tendon is at an angle of 25.0° with the tibia, assuming that w = 29.0 N, F = 12.3 N, and the leg is extended at an angle ? of 40.0° with the vertical. Assume that the center of gravity of the lower leg is at its center and that the tendon attaches to the lower leg at a point one-fifth of the way down the leg. (Give the magnitude.)arrow_forwardThe bones of the forearm (radius and ulna) are hinged to the humerus at the elbow. The biceps muscle connects to the bones of the forearm about 2.15 cm beyond the joint. Biceps muscle Assume the forearm has a mass of 2.25 kg and a length of 0.425 m. When the humerus and the biceps are nearly vertical and the forearm is horizontal, if a person wishes to Humerus hold an object of mass 6.55 kg so that her forearm remains motionless, what is the force exerted by the biceps muscle? Radius Elbow. Ulna force: N Handarrow_forwardWhen a gymnast weighing 740 N executes the iron cross as in figure (a), the primary muscles involved in supporting this position are the latissimus dorsi ("lats") and the pectoralis major ("pecs"). The rings exert an upward force on the arms and support the weight of the gymnast. The force exerted by the shoulder joint on the arm is labeled F while the two muscles exert a total force F on the arm. Determine the magnitude of the force F Note that one ring supports half the weight of the gymnast, which is w 370 N as indicated in figure (b). Assume that the force F acts at an angle of 45° below the horizontal at a distance of 4.0 cm from the shoulder joint. In your estimate, take the distance from the shoulder joint to the hand to be L = 75 cm and ignore the weight of the arm. m kN Shoulder joint 4.0 cm- 45.00 Ed Bock/CORBISarrow_forward
- The bones of the forearm (radius and ulna) are hinged to the humerus at the elbow. The biceps muscle connects to the bones of the forearm about 2.15 cm beyond the joint. Assume the forearm has a mass of 2.25 kg and a length of 0.425 m. When the humerus and the biceps are nearly vertical and the forearm is horizontal, if a person wishes to hold an object of mass 6.95 kg so that her forearm remains motionless, what is the force ? exerted by the biceps muscle? ?=arrow_forwardA person who weighs 775 N supports himself on the ball of one foot. The normal force N = 775 N pushes up on the ball of the foot on one side of the ankle joint, while the Achilles tendon pulls up on the foot on the other side of the joint. The center of gravity of the person is located right above the tibia. What is the tension in the Achilles tendon? If the force acting is upward, enter a positive value and if the force acting is downward, enter a negative value.arrow_forwardWhen you bend over, a series of large muscles, the erector spinae, pull on your spine to hold you up. Figure shows a simplified model of the spine as a rod of length L that pivots at its lower end. In this model, the center of gravity of the 320 N weight of the upper torso is at the center of the spine. The 160 N weight of the head and arms acts at the top of the spine. The erector spinae muscles are modeled as a single muscle that acts at an 12° angle to the spine. Suppose the person shown bends over to an angle of 30° from the horizontal. a. What is the tension in the erector muscle? Hint: Align your x-axis with the axis of the spine.b. A force from the pelvic girdle acts on the base of the spine. What is the component of this force in the direction of the spine? (This large force is the cause of many back injuries).arrow_forward
- Everett is attempting to lift 112 N. The perpendicular distance from the weight to his elbow joint is 21 cm. Theforce created by the elbow flexor muscles is 1485 N. The perpendicular distance from this force to the elbow jointis 1.8 cm. Is Everett able to lift the weight with this amount of force in his flexor muscles?arrow_forwardA 35 N forearm (we are ignoring the hand for this problem) are held at a 45 deg angle to the vertically oriented humerus. The COM of the forearm is located at a distance of 15 cm from the joint center at the elbow, and the elbow flexor muscles have a 3 cm moment arm. How much force must be exerted by the elbow flexor muscles to maintain this position? Hide answer choices A A 35 N C 81.7 N 123.7 N D 371 N Fm 45° * --Wt₂arrow_forwardAn individual leans forwards to pick up a box of 100 N. The weight of his upper body has a magnitude of 450 N. The back is pivoting around the base of the vertebral column. Consider the back of the individual as a rigid bar that is controlled by a muscle with an angle of 12° (See picture, d = trunk-head distance = 1 m).a) Calculate the magnitude of muscle force required to lift the box.b) Calculate the magnitude of the force at the base of the vertebral column. Hints: For (a) solve the equilibrium of moments, i.e. what force is required in the muscle to balance out the moments acting around the base of the spine.For (b), solve the equilibrium of forces acting on the spine, including the muscle force you’ve just calculated, in x and y separately. There are two extra forces not shown in the diagram: x and y contact forces acting at the base of the spine. These are whatever is needed to keep the total forces acting on the spine = 0 (so the spine isn’t accelerating off in some…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON
Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON
What is Torque? | Physics | Extraclass.com; Author: Extraclass Official;https://www.youtube.com/watch?v=zXxrAJld9mo;License: Standard YouTube License, CC-BY