
Calculus (MindTap Course List)
8th Edition
ISBN: 9781285740621
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 9.6, Problem 6E
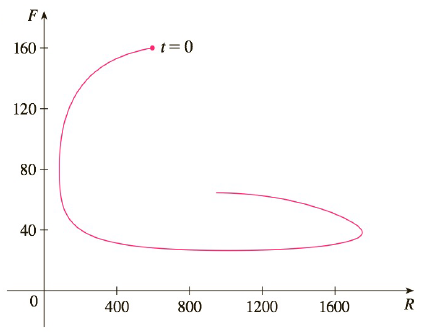
5–6 A phase trajectory is shown for populations of rabbits (R) and foxes (F).
(a) Describe how each population changes as time goes by.
(b) Use your description to make a rough sketch of the graphs of R and F as functions of time.
 .
.
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
Exer. 31-32: Find an exponential function of the form
f(x) = ba-* + c that has the given horizontal asymptote and
y-intercept and passes through point P.
31 y = 32; y-intercept 212; P(2, 112)
32 y = 72; y-intercept 425; P(1, 248.5)
y = 4
(1, 2.5)
(0, 2)
Pictured above is the graph of a function of the form y = Ca" + b. Find C, a, and b.
In example 4, we investigated Holling’s disk equation.
P=(aN)/(1+aTN)
We will now consider P as a function of the predator attack rate a. Determine how the predator attack rate a influences the number of prey eaten per predator.
Chapter 9 Solutions
Calculus (MindTap Course List)
Ch. 9.1 - Show that y=23ex+e2x is a solution of the...Ch. 9.1 - Verify that y=tcostt is a solution of the...Ch. 9.1 - a For what values of r does the function y=erx...Ch. 9.1 - Prob. 4ECh. 9.1 - Which of the following functions are solutions of...Ch. 9.1 - a Show that every member of the family of...Ch. 9.1 - a What can you say about a solution of the...Ch. 9.1 - a What can you say about the graph of a solution...Ch. 9.1 - Prob. 9ECh. 9.1 - The Fitzhugh-Nagumo model for the electrical...
Ch. 9.1 - Explain why the functions with the given graphs...Ch. 9.1 - The function with the given graph is a solution of...Ch. 9.1 - Match the differential equations with the solution...Ch. 9.1 - Suppose you have just poured a cup of freshly...Ch. 9.1 - Prob. 15ECh. 9.1 - Von Bertalanffys equation states that the rate of...Ch. 9.1 - Differential equations have been used extensively...Ch. 9.2 - A direction field for the differential equation...Ch. 9.2 - A direction field for the differential equation...Ch. 9.2 - Prob. 3ECh. 9.2 - Prob. 4ECh. 9.2 - 36 Match the differential equation with its...Ch. 9.2 - 36 Match the differential equation with its...Ch. 9.2 - Prob. 7ECh. 9.2 - Prob. 8ECh. 9.2 - Prob. 9ECh. 9.2 - 910 Sketch a direction field for the differential...Ch. 9.2 - Prob. 11ECh. 9.2 - Prob. 12ECh. 9.2 - Prob. 13ECh. 9.2 - Prob. 14ECh. 9.2 - Prob. 15ECh. 9.2 - Prob. 16ECh. 9.2 - Use a computer algebra system to draw a direction...Ch. 9.2 - Make a rough sketch of a direction field for the...Ch. 9.2 - a Use Eulers method with each of the following...Ch. 9.2 - A direction field for a differential equation is...Ch. 9.2 - Prob. 21ECh. 9.2 - Prob. 22ECh. 9.2 - Use Eulers method with step size 0.1 to estimate...Ch. 9.2 - Prob. 24ECh. 9.2 - a Program a calculator or computer to use Eulers...Ch. 9.2 - a Program your computer algebra system, using...Ch. 9.2 - The figure shows a circuit containing an...Ch. 9.2 - In Exercise 9.1.14 we considered a 95C cup of...Ch. 9.3 - 110 Solve the differential equation. dydx=3x2y2Ch. 9.3 - Prob. 2ECh. 9.3 - Prob. 3ECh. 9.3 - 110 Solve the differential equation. y+xey=0Ch. 9.3 - Prob. 5ECh. 9.3 - Prob. 6ECh. 9.3 - Prob. 7ECh. 9.3 - Prob. 8ECh. 9.3 - Prob. 9ECh. 9.3 - Prob. 10ECh. 9.3 - 1118 Find the solution of the differential...Ch. 9.3 - Prob. 12ECh. 9.3 - Prob. 13ECh. 9.3 - Prob. 14ECh. 9.3 - 1118 Find the solution of the differential...Ch. 9.3 - Prob. 16ECh. 9.3 - Prob. 17ECh. 9.3 - Prob. 18ECh. 9.3 - Find an equation of the curve that passes through...Ch. 9.3 - Find the function f such that...Ch. 9.3 - Prob. 21ECh. 9.3 - Prob. 22ECh. 9.3 - Prob. 23ECh. 9.3 - Prob. 24ECh. 9.3 - Prob. 25ECh. 9.3 - Prob. 26ECh. 9.3 - a Use a computer algebra system to draw a...Ch. 9.3 - 2728 a Use a computer algebra system to draw a...Ch. 9.3 - 2932 Find the orthogonal trajectories of the...Ch. 9.3 - 2932 Find the orthogonal trajectories of the...Ch. 9.3 - 2932 Find the orthogonal trajectories of the...Ch. 9.3 - 2932 Find the orthogonal trajectories of the...Ch. 9.3 - 3335 An integral equation is an equation that...Ch. 9.3 - 3335 An integral equation is an equation that...Ch. 9.3 - Prob. 35ECh. 9.3 - Find a function f such that f(3)=2 and...Ch. 9.3 - Prob. 37ECh. 9.3 - In Exercise 9.2.28 we discussed a differential...Ch. 9.3 - Prob. 39ECh. 9.3 - In an elementary chemical reaction, single...Ch. 9.3 - In contrast to the situation of Exercise 40,...Ch. 9.3 - Prob. 42ECh. 9.3 - Prob. 43ECh. 9.3 - A certain small country has 10 billion in paper...Ch. 9.3 - Prob. 45ECh. 9.3 - Prob. 46ECh. 9.3 - A vat with 500 gallons of beer contains 4 alcohol...Ch. 9.3 - A tank contains 1000 L of pure water. Brine that...Ch. 9.3 - Prob. 49ECh. 9.3 - An object of mass m is moving horizontally through...Ch. 9.3 - Prob. 51ECh. 9.3 - Prob. 52ECh. 9.3 - Let A(t) be the area of a tissue culture at time t...Ch. 9.3 - Prob. 54ECh. 9.4 - 12 A population grows according to the given...Ch. 9.4 - 1-2 A population grows according to the given...Ch. 9.4 - Suppose that a population develops according to...Ch. 9.4 - Suppose that a population grows according to a...Ch. 9.4 - The Pacific halibut fishery has been modeled by...Ch. 9.4 - Suppose a population P(t) satisfies...Ch. 9.4 - Suppose a population grows according to a logistic...Ch. 9.4 - The table gives the number of yeast cells in a new...Ch. 9.4 - Prob. 9ECh. 9.4 - Prob. 10ECh. 9.4 - One model for the spread of a rumor is that the...Ch. 9.4 - Biologists stocked a lake with 400 fish and...Ch. 9.4 - Prob. 13ECh. 9.4 - Prob. 14ECh. 9.4 - Prob. 15ECh. 9.4 - Prob. 16ECh. 9.4 - Consider a population P=P(t) with constant...Ch. 9.4 - Let c be a positive number. A differential...Ch. 9.4 - Lets modify the logistic differential equation of...Ch. 9.4 - Consider the differential equation...Ch. 9.4 - There is considerable evidence to support the...Ch. 9.4 - Prob. 22ECh. 9.4 - In a seasonal-growth model, a periodic function of...Ch. 9.4 - Prob. 24ECh. 9.4 - Prob. 25ECh. 9.5 - 14 Determine whether the differential equation is...Ch. 9.5 - Prob. 2ECh. 9.5 - Prob. 3ECh. 9.5 - Prob. 4ECh. 9.5 - 514 Solve the differential equation. y+y=1Ch. 9.5 - 514 Solve the differential equation. yy=exCh. 9.5 - 514 Solve the differential equation. y=xyCh. 9.5 - 514 Solve the differential equation....Ch. 9.5 - Prob. 9ECh. 9.5 - Prob. 10ECh. 9.5 - Prob. 11ECh. 9.5 - Prob. 12ECh. 9.5 - Prob. 13ECh. 9.5 - Prob. 14ECh. 9.5 - Prob. 15ECh. 9.5 - Prob. 16ECh. 9.5 - Prob. 17ECh. 9.5 - Prob. 18ECh. 9.5 - 1520 Solve the initial-value problem....Ch. 9.5 - Prob. 20ECh. 9.5 - Prob. 21ECh. 9.5 - Prob. 22ECh. 9.5 - A Bernoulli differential equation named after...Ch. 9.5 - 2425 Use the method of Exercise 23 to solve the...Ch. 9.5 - Prob. 25ECh. 9.5 - Prob. 26ECh. 9.5 - Prob. 27ECh. 9.5 - Prob. 28ECh. 9.5 - Prob. 29ECh. 9.5 - Prob. 30ECh. 9.5 - Prob. 31ECh. 9.5 - Prob. 32ECh. 9.5 - In Section 9.3 we looked at mixing problems in...Ch. 9.5 - Prob. 34ECh. 9.5 - An object with mass m is dropped from rest and we...Ch. 9.5 - If we ignore air resistance, we can conclude that...Ch. 9.5 - Prob. 37ECh. 9.5 - To account for seasonal variation in the logistic...Ch. 9.6 - For each predator-prey system, determine which of...Ch. 9.6 - Each system of differential equations is a model...Ch. 9.6 - Prob. 3ECh. 9.6 - Prob. 4ECh. 9.6 - 56 A phase trajectory is shown for populations of...Ch. 9.6 - 56 A phase trajectory is shown for populations of...Ch. 9.6 - 78 Graphs of populations of two species are shown....Ch. 9.6 - Prob. 8ECh. 9.6 - Prob. 9ECh. 9.6 - Populations of aphids and ladybugs are modeled by...Ch. 9.6 - In Example 1 we used Lotka-Volterra equations to...Ch. 9.6 - In Exercise 10 we modeled populations of aphids...Ch. 9.R - Prob. 1CCCh. 9.R - Prob. 2CCCh. 9.R - Prob. 3CCCh. 9.R - Prob. 4CCCh. 9.R - Prob. 5CCCh. 9.R - Prob. 6CCCh. 9.R - Prob. 7CCCh. 9.R - Prob. 8CCCh. 9.R - a Write Lotka-Volterra equations to model...Ch. 9.R - Prob. 1TFQCh. 9.R - Prob. 2TFQCh. 9.R - Prob. 3TFQCh. 9.R - Determine whether the statement is true or false....Ch. 9.R - Prob. 5TFQCh. 9.R - Determine whether the statement is true or false....Ch. 9.R - Prob. 7TFQCh. 9.R - Prob. 1ECh. 9.R - a Sketch a direction field for the differential...Ch. 9.R - a A direction field for the differential equation...Ch. 9.R - Prob. 4ECh. 9.R - Prob. 5ECh. 9.R - Prob. 6ECh. 9.R - 58 Solve the differential equation. 2yey2y=2x+3xCh. 9.R - 58 Solve the differential equation. x2yy=2x3e1/xCh. 9.R - 911 Solve the initial-value problem....Ch. 9.R - 911 Solve the initial-value problem....Ch. 9.R - Prob. 11ECh. 9.R - Prob. 12ECh. 9.R - 1314 Find the orthogonal trajectories of the...Ch. 9.R - Prob. 14ECh. 9.R - Prob. 15ECh. 9.R - a The population of the world was 6.1 billion in...Ch. 9.R - Prob. 17ECh. 9.R - Prob. 18ECh. 9.R - One model for the spread of an epidemic is that...Ch. 9.R - Prob. 20ECh. 9.R - Prob. 21ECh. 9.R - Populations of birds and insects are modeled by...Ch. 9.R - Prob. 23ECh. 9.R - Prob. 24ECh. 9.P - Find all functions f such that f is continuous and...Ch. 9.P - Prob. 2PCh. 9.P - Prob. 3PCh. 9.P - Find all functions f that satisfy the equation...Ch. 9.P - Prob. 5PCh. 9.P - A subtangent is a portion of the x-axis that lies...Ch. 9.P - A peach pie is taken out of the oven at 5:00 PM....Ch. 9.P - Snow began to fall during the morning of February...Ch. 9.P - A dog sees a rabbit running in a straight line...Ch. 9.P - a Suppose that the dog in Problem 9 runs twice as...Ch. 9.P - A planning engineer for a new alum plant must...Ch. 9.P - Prob. 12PCh. 9.P - Prob. 13PCh. 9.P - Prob. 14PCh. 9.P - Prob. 15PCh. 9.P - a An outfielder fields a baseball 280 ft away from...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- question 8arrow_forwardActivity 3.5.4. As pictured in the applet at http://gvsu.edu/s/9q, a skateboarder who is 6 feet tall rides under a 15 foot tall lamppost at a constant rate of 3 feet per second. We are interested in understanding how fast his shadow is changing at various points in time. a. Draw an appropriate right triangle that represents a snapshot in time of the skateboarder, lamppost, and his shadow. Let x denote the horizontal distance from the base of the lamppost to the skateboarder and s represent the length of his shadow. Label these quantities, as well as the skateboarder's height and the lamppost's height on the diagram. b. Observe that the skateboarder and the lamppost represent parallel line segments in the diagram, and thus similar triangles are present. Use similar triangles to establish an equation that relates x and s. c. Use your work in (b) to find an equation that relates and . d. At what rate is the length of the skateboarder's shadow increasing at the instant the skateboarder is…arrow_forward1arrow_forward
- NR. 3arrow_forwardThe longitude, rt of an air plane is affected by a random component e, due to the wind effect and its speed t It = -1 + 20t-1 + 6t. The speed of the plane is affected by a constant global linear trend, ß = B₁-1 = 3, and varies randomly due to weather conditions, v₁ = V₁-1 + B₁-1+w₂. In the above equations, is assumed to be white Gaussian noise with zero mean and o = 3. Similarly w is assumed to be white Gaussian noise with zero mean and 2,=0.5. A GPS transmitter mounted on the plane sends a noisy measurement to a receiver about its position, X₁ = 0.5xt + nt, where n, is assumed to be white Gaussian noise with zero mean and o2 = 2. (a) Using the following definition for the state vector, 0t. 0₁ It + ve B₂ write the motion of the plane in state space form. Note: You need to provide the exact form of the h, G and W matrices. (b) Evaluate the initial estimate for the state vector 03-arrow_forwardQuestion 5 1 pts At the beginning of the semester, procrastinators reported an average of 0.8 symptoms, increasing at a rate of 0.45 symptoms, per week. Choose the function that models the average number of symptoms, y, after x weeks. Oy= 0.45x+0.8 Oy 0.8x+0.45 O 0.8 = y+0.45x 0.45 y+0.8 Question 6 1 ptsarrow_forward
- Question 2a) urgentlyarrow_forwardQuestion 20 The temperatures of component A and component B in a heat exchanger vary in a linear fashion as shown in the graph below, where y is the temperature in °C, after x minutes. 72 (b) -20- 10 24 (a) Determine a rule for the temperature of component A in terms of x. Showing full working, determine when both components are at the same temperature, and state what this temperature is.arrow_forwardNumber 7arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY