Chapter 9, Problem 9.7.3P

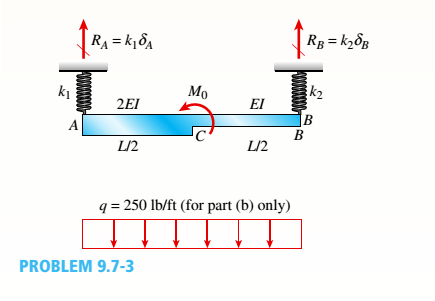
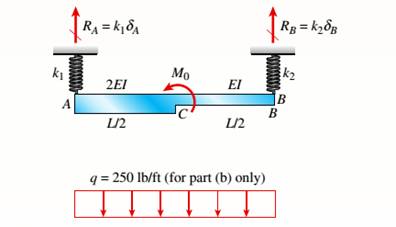
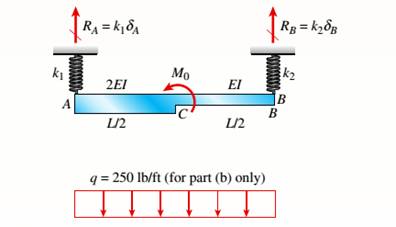
Beam ACB hangs from two springs, as shown in the figure. The springs have stiffnesses Jt₍and k₂^ and the beam has flexural rigidity EI.

1. What is the downward displacement of point C, which is at the midpoint of the beam, when the moment M_Qis applied? Data for the structure are M₀ = 7.5 kip-ft, L = 6 ft, EI = 520 kip-ft², k_x= 17 kip/ft, and As = 11 kip/ft.
2. Repeat part (a), but remove Af₀ and instead apply uniform load q over the entire beam.

  

To determine

The downward displacement of point C of the beam.

Answer to Problem 9.7.3P

The downward displacement of point C is $-0.31\text{ in}\text{.}$

Explanation of Solution

Given:

We have the data,

  $\begin{array}{l}{M}_0=7.5k\cdot ft\\ L=6ft\\ EI=520\text{ k}\cdot {\text{ft}}^2\\ k_1=17\text{ k/ft}\\ {\text{k}}_2=11\text{ k/ft}\end{array}$

Concept Used:

Beam ACB hangs fro two springs which have stifness $k_{1\text{}}{\text{ and k}}_2$ and the beam has a felxural rigidity EI.

  

Calculation:

We can write bending moment equations −moment at Point C as follows:

  $\begin{array}{l}For\left(0\le x\le \frac{L}{2}\right);\\ 2EI{v}^{"\text{'}}=M\\ 2EI{v}^{"\text{'}}=\frac{M_{0}x}{L}\end{array}$

To determine slope equation, we are integrating the above equation, we will get,

  $2EI{v}^{\text{'}}=\frac{M_0{x}^2}{2L}+C_1$

To determine deflection equation, we are integrating the above equation, we will get,

  $2EIv=\frac{M_0{x}^3}{6L}+C_{1}x+C_2$

Now applying the boundary conditions to find out the constants as follows:

  $\begin{array}{l}\text{For v}\left(0\right)=0{\text{ and C}}_2=0\\ 2EIv=\frac{M_0{x}^3}{6L}+C_{1}x\end{array}$

  $\begin{array}{l}For\left(\frac{L}{2}\le x\le L\right)L;\\ EI{v}^{"\text{'}}=-\frac{M_0}{2}+\frac{M_0\left(x-\frac{L}{2}\right)}{L}\\ EI{v}^{"\text{'}}=-M_0+\frac{M_{0}x}{L}\end{array}$

To determine slope equation, we are integrating the above equation, we will get,

  $EI{v}^{\text{'}}=-M_{0}x+\frac{M_0{x}^2}{2L}+C_3$

To determine deflection equation, we are integrating the above equation, we will get,

  $EIv=-\frac{M_0{x}^2}{2}+\frac{M_0{x}^3}{6L}+C_{3}x+C_4$

Now applying the boundary conditions to find out the constants as follows:

  $\begin{array}{l}\text{For v}\left(0\right)=0\text{ and x =L}\\ 0=-\frac{M_0{L}^2}{2}+\frac{M_0{L}^3}{6L}+C_{3}L+C_4\mathrm{.......}(1)\\ {\text{At v}}_L{}^{\text{'}}\left(\frac{L}{2}\right)=v_R{}^{\text{'}}\left(\frac{L}{2}\right):\\ \frac{1}{2}\left[\frac{M_0{\left(\frac{L}{2}\right)}^2}{2L}+C_1\right]=-M_0\frac{L}{2}+\frac{M_0{\left(\frac{L}{2}\right)}^2}{2L}+C_3\mathrm{.......}(2)\\ {\text{At v}}_L\left(\frac{L}{2}\right)=v_R\left(\frac{L}{2}\right):\\ \frac{1}{2}\left[\frac{M_0{\left(\frac{L}{2}\right)}^3}{6L}+C_1\left(\frac{L}{2}\right)\right]=-\frac{M_0{\left(\frac{L}{2}\right)}^2}{2}+\frac{M_0{\left(\frac{L}{2}\right)}^3}{6L}+C_3\left(\frac{L}{2}\right)+C_4\mathrm{.......}(3)\end{array}$

Now we will get the below values after solving equations (1), (2) and (3).

  $\begin{array}{l}{C}_1=0\\ C_3=\frac{7}{16}{M}_{0}L\\ C_4=\frac{-5}{48}{M}_0{L}^2\end{array}$

In deflection equation, we are putting values of $C_1$ ,

  $\begin{array}{l}\text{For }\left(0\le x\le \frac{L}{2}\right).\\ 2EIv\left(x\right)=\frac{M_0{x}^3}{6L}+\left(0\right)x\\ v\left(x\right)=\frac{M_0{x}^3}{12EIL}\end{array}$

Once again in deflection equation, putting values of $C_3=\frac{7}{16}{M}_{0}L\text{ and }{C}_4=\frac{-5}{48}{M}_0{L}^2$ ,

  $\begin{array}{l}\text{For }\left(\frac{L}{2}\le x\le L\right).\\ EIv\left(x\right)=-\frac{M_0{x}^2}{2}+\frac{M_0{x}^3}{6L}+\left(\frac{7}{16}{M}_{0}L\right)x+\left(\frac{-5}{48}{M}_0{L}^2\right)\\ v\left(x\right)=\frac{M_0}{48EIL}\left(24x^{2}L+8x^3+21L^{2}x-5L^3\right)\end{array}$

Now calculating, the reactions at supports:

  $\begin{array}{l}{R}_A=\frac{M_0}{L}\\ R_B=-\frac{M_0}{L}\end{array}$

We can determine deflection at point A below.

  $\begin{array}{l}{\delta }_A=\frac{R_A}{k_1}\\ {\delta }_A=\frac{M_0}{k_{1}L}\\ {\delta }_A=\frac{7.5}{17\times 6}\\ {\delta }_A=0.07353\text{}\text{ ft}\left(\frac{12\text{ in}\text{.}}{1\text{}\text{ft}}\right)\\ {\delta }_A=0.882\text{}\text{in}\text{.}(\downarrow )\end{array}$

We can determine deflection at point B below.

  $\begin{array}{l}{\delta }_B=\frac{R_B}{k_1}\\ {\delta }_B=-\frac{M_0}{k_{2}L}\\ {\delta }_B=-\frac{7.5}{11\times 6}\\ {\delta }_B=-0.1136\text{}\text{ ft}\left(\frac{12\text{ in}\text{.}}{1\text{}\text{ft}}\right)\\ {\delta }_B=-1.363\text{}\text{in}\text{.}(\downarrow )\end{array}$

We can determine deflection at point C as below.

  $\begin{array}{l}{\delta }_C=-v\left(\frac{L}{2}\right)+\frac{1}{2}\left({\delta }_A+{\delta }_B\right)\\ {\delta }_C=-\frac{M_0{\left(\frac{L}{2}\right)}^3}{12EIL}+\frac{1}{2}\left({\delta }_A+{\delta }_B\right)\\ {\delta }_C=-\frac{7.5{\left(\frac{6}{2}\right)}^3}{12\left(520\right)6}+\frac{1}{2}\left(0.07353+\left(-0.1136\right)\right)\\ {\delta }_C=-0.02544\text{ ft}\left(\frac{12\text{ in}\text{.}}{1\text{ft }}\right)\\ {\delta }_C=-0.31\text{ in}\text{.}(\uparrow )\end{array}$

Therefore, we have determined the downward displacement of point C is $-0.31\text{ in}\text{.}$

Conclusion:

The downward displacement of point C is calculated using deflection equation.

To determine

The downward displacement of point C of the beam.

Answer to Problem 9.7.3P

The downward displacement of point C is $0.762\text{ in}\text{.}$

Explanation of Solution

Given:

We have the data,

  $\begin{array}{l}L=6ft\\ EI=520\text{ k}\cdot {\text{ft}}^2\\ k_1=17\text{ k/ft}\\ {\text{k}}_2=11\text{ k/ft}\end{array}$

Concept Used:

Beam ACB hangs fro two springs which have stifness $k_{1\text{}}{\text{ and k}}_2$ and the beam has a felxural rigidity EI.

  

Calculation:

We can write bending moment equations −with uniform load q at Point C as follows:

  $\begin{array}{l}For\left(0\le x\le \frac{L}{2}\right);\\ 2EI{v}^{"\text{'}}=M\\ 2EI{v}^{"\text{'}}=\frac{qLx}{2}-\frac{q{x}^2}{2}\end{array}$

To determine slope equation, we are integrating the above equation, we will get,

  $2EI{v}^{\text{'}}=\frac{qL{x}^2}{4}-\frac{q{x}^3}{6}+C_1$

To determine deflection equation, we are integrating the above equation, we will get,

  $2EIv=\frac{qL{x}^3}{12}-\frac{q{x}^4}{24}+C_{1}x+C_2$

Now applying the boundary conditions to find out the constants as follows:

  $\begin{array}{l}\text{For v}\left(0\right)=0{\text{ and C}}_2=0\\ 2EIv=\frac{qL{x}^3}{12}-\frac{q{x}^4}{24}+C_{1}x\end{array}$

  $\begin{array}{l}For\left(\frac{L}{2}\le x\le L\right)L;\\ EI{v}^{"\text{'}}=\frac{qLx}{2}-\frac{q{x}^2}{2}\end{array}$

To determine slope equation, we are integrating the above equation, we will get,

  $EI{v}^{\text{'}}=\frac{qL{x}^2}{4}-\frac{q{x}^3}{6}+C_3$

To determine deflection equation, we are integrating the above equation, we will get,

  $EIv=\frac{qL{x}^3}{12}-\frac{q{x}^4}{24}+C_{3}x+C_4$

Now applying the boundary conditions to find out the constants as follows:

  $\begin{array}{l}\text{For v}\left(0\right)=0\text{ and x =L}\\ \frac{qL{L}^3}{12}-\frac{q{L}^4}{24}+C_{3}x+C_4\mathrm{......}(4)\\ {\text{At v}}_L{}^{\text{'}}\left(\frac{L}{2}\right)=v_R{}^{\text{'}}\left(\frac{L}{2}\right):\\ \frac{1}{2}\left[\frac{qL{\left(\frac{L}{2}\right)}^2}{4}-\frac{qL{\left(\frac{L}{2}\right)}^3}{6}+C_1\right]=\frac{qL{\left(\frac{L}{2}\right)}^2}{4}-\frac{qL{\left(\frac{L}{2}\right)}^2}{6}+C_3\mathrm{.......}(5)\\ {\text{At v}}_L\left(\frac{L}{2}\right)=v_R\left(\frac{L}{2}\right):\\ \frac{1}{2}\left[\frac{qL{\left(\frac{L}{2}\right)}^3}{12}-\frac{qL{\left(\frac{L}{2}\right)}^4}{24}+C_1\left(\frac{L}{2}\right)\right]=\frac{qL{\left(\frac{L}{2}\right)}^3}{12}-\frac{qL{\left(\frac{L}{2}\right)}^4}{24}+C_3\left(\frac{L}{2}\right)+C_4\mathrm{.......}(6)\end{array}$

Now we will get the below values after solving equations (4), (5) and (6).

  $\begin{array}{l}{C}_1=\frac{-7}{128}q{L}^3\\ C_3=\frac{-37}{7686}q{L}^3\\ C_4=\frac{5}{768}q{L}^4\end{array}$

In deflection equation, we are putting values of $C_1$ ,

  $\begin{array}{l}\text{For }\left(0\le x\le \frac{L}{2}\right).\\ v\left(x\right)=-\frac{qx}{768EI}\left(-32L{x}^2+16x^3+21L^3\right)\end{array}$

Once again in deflection equation, putting values of $C_3=\frac{-37}{7686}q{L}^3\text{and }{C}_4=\frac{5}{768}q{L}^4$ ,

  $\begin{array}{l}\text{For }\left(\frac{L}{2}\le x\le L\right).\\ v\left(x\right)=\frac{q}{768EI}\left(64L{x}^3-32x^2-37L^{3}x+5L^4\right)\end{array}$

Now calculating, the reactions at supports:

  $\begin{array}{l}{R}_A=\frac{qL}{2}\\ R_B=-\frac{qL}{2}\end{array}$

We can determine deflection at point A as below.

  $\begin{array}{l}{\delta }_A=\frac{R_A}{k_1}\\ {\delta }_A=\frac{qL}{2k_1}\\ {\delta }_A=\frac{250\times 6}{2\times 17\times {10}^3}\\ {\delta }_A=0.0441\text{}\text{ ft}\left(\frac{12\text{ in}\text{.}}{1\text{}\text{ft}}\right)\\ {\delta }_A=0.53\text{}\text{in}\text{.}(\downarrow )\end{array}$

We can determine deflection at point B below.

  $\begin{array}{l}{\delta }_B=\frac{R_B}{k_1}\\ {\delta }_B=\frac{qL}{2k_2}\\ {\delta }_B=\frac{250\times 6}{2\times 11\times {10}^3}\\ {\delta }_B=0.0709\text{}\text{ ft}\left(\frac{12\text{ in}\text{.}}{1\text{}\text{ft}}\right)\\ {\delta }_B=0.85\text{}\text{in}\text{.}(\downarrow )\end{array}$

We can determine deflection at point C below.

  $\begin{array}{l}{\delta }_C=-v\left(\frac{L}{2}\right)+\frac{1}{2}\left({\delta }_A+{\delta }_B\right)\\ {\delta }_C=\frac{qL\left(\frac{L}{2}\right)}{768EI}\left[-32L{\left(\frac{L}{2}\right)}^2+16{\left(\frac{L}{2}\right)}^3+21L^3\right]+\frac{1}{2}\left({\delta }_A+{\delta }_B\right)\\ {\delta }_C=\frac{250\left(\frac{6}{2}\right)}{768\times \left(520\times 10\right)}\left[-32\times 6{\left(\frac{6}{2}\right)}^2+16{\left(\frac{6}{2}\right)}^3+21{\left(6\right)}^3\right]+\frac{1}{2}\left(0.0441+0.0709\right)\\ {\delta }_C=0.0635\text{ ft}\left(\frac{12\text{ in}\text{.}}{1\text{ft }}\right)\\ {\delta }_C=0.762\text{ in}\text{.}(\downarrow )\end{array}$

Therefore, we have determined the downward displacement of point C is $0.762\text{ in}\text{.}$

Conclusion:

The downward displacement of point C is calculated by this formula : $\begin{array}{l}{\delta }_C=-v\left(\frac{L}{2}\right)+\frac{1}{2}\left({\delta }_A+{\delta }_B\right)\\ \end{array}$