Chapter 9, Problem 9.7.2P

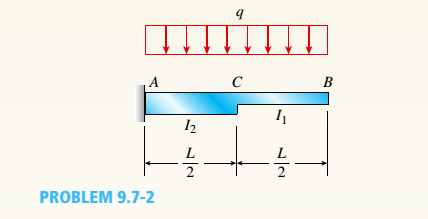
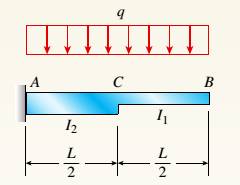
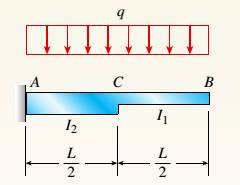
The cantilever beam ACB shown in the figure supports a uniform load of intensity q throughout its length. The beam has moments of inertia I₂and I_Yin parts AC and CB, respectively.

1. Using the method of superposition, determine the deflection S_Bat the free end due to the uniform load.

Determine the ratio r of the deflection 6_Bto the deflection 3_Xat the free end of a prismatic cantilever with moment of inertia /] carrying the same load.

Plot a graph of the deflection ratio r versus the ratio 12 //_t of the moments of inertia. (Let 7, tl_xvary from I to 5.)

  

To determine

The deflectiony13 ${\delta }_B$ at the free end of beam due to load P using method of superposition.

Answer to Problem 9.7.2P

The deflectiony1313 ${\delta }_B$ is ${\delta }_B=\frac{q{L}^4}{128E{I}_1}\left[1+\frac{15I_1}{I_2}\right]$ at the free end of beam due to load P using method of superposition.

Explanation of Solution

Given:

We have the data,

Length of the beam ACB as, L

Intensity of uniform load, q

Moment of inertia of,

  $AC=I_2$

Moment of inertia of, $BC=I_1$

  $AC=CB=\frac{L}{2}$

Concept Used:

The cantilever beam ACB as per the below figure supports a uniform load of intensity q throughout its length with moments of inertia $I_2{\text{ and I}}_1$ in parts of AC and CB.

  

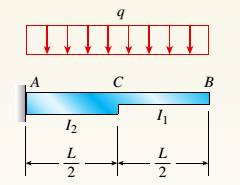
Calculation:

We have the below diagram for part CB as below.

  

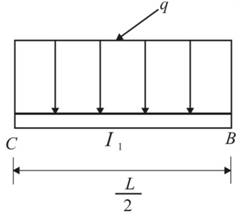
Deflection at point B would be calculated as,

  $\begin{array}{l}{\left({\delta }_B\right)}_1=\frac{q}{8E{I}_i}{\left(\frac{L}{2}\right)}^4\\ {\left({\delta }_B\right)}_1=\frac{q{L}^4}{128E{I}_1}\end{array}$

We have the below diagram for part AC as below.

  

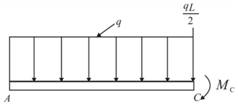
The moment at point C,

  $M_C=\frac{q{L}^2}{8}$

The deflection at point C can be calculated as below.

  $\begin{array}{l}{\delta }_C=\frac{q{\left(\frac{L}{2}\right)}^4}{8E{I}_2}+\frac{\frac{q{L}^{}}{2}{\left(\frac{L}{2}\right)}^3}{3E{I}_2}+\frac{M_C{\left(\frac{L}{2}\right)}^2}{2E{I}_2}\\ {\delta }_C=\frac{q{L}^4}{128E{I}_2}+\frac{q{L}^4}{48E{I}_2}+\frac{\left(\frac{q{L}^2}{8}\right)\left(\frac{L^2}{4}\right)}{2E{I}_2}\\ {\delta }_C=\frac{q{L}^4}{128E{I}_2}+\frac{q{L}^4}{48E{I}_2}+\frac{q{L}^4}{64E{I}_2}\\ .{\delta }_C=\frac{3q{L}^4+8q{L}^4+6q{L}^4}{384E{I}_2}\\ {\delta }_C=\frac{17q{L}^4}{384E{I}_2}\end{array}$

Angle of rotation at point C can be determined as,

  $\begin{array}{l}{\theta }_C=\frac{q{\left(\frac{L}{2}\right)}^2}{6E{I}_2}+\frac{\left(\frac{qL}{2}\right){\left(\frac{L}{2}\right)}^2}{2E{I}_2}+\frac{{\left(\frac{qL}{8}\right)}^2{\left(\frac{L}{2}\right)}^2}{E{I}_2}\\ {\theta }_C=\frac{q{L}^3}{48E{I}_2}+\frac{q{L}^3}{16E{I}_2}+\frac{q{L}^3}{16E{I}_2}\\ .{\theta }_C=\frac{q{L}^3+3q{L}^3+3q{L}^3}{48E{I}_2}\\ {\theta }_C=\frac{7q{L}^3}{48E{I}_2}\end{array}$

At point B, the deflection would be,

  $\begin{array}{l}{\left({\delta }_B\right)}_2={\delta }_C+{\theta }_C\left(\frac{L}{2}\right)\\ {\left({\delta }_B\right)}_2=\frac{17q{L}^4}{384E{I}_2}+\frac{7q{L}^3}{48E{I}_2}\left(\frac{L}{2}\right)\\ {\left({\delta }_B\right)}_2=\frac{17q{L}^4}{384E{I}_2}+\frac{7q{L}^4}{96E{I}_2}\\ {\left({\delta }_B\right)}_2=\frac{17q{L}^4+28q{L}^4}{384E{I}_2}\\ {\left({\delta }_B\right)}_2=\frac{45q{L}^4}{384E{I}_2}\\ {\left({\delta }_B\right)}_2=\frac{15q{L}^4}{128E{I}_2}\end{array}$

Therefore, the total deflection at point B would be,

  $\begin{array}{l}{\delta }_B={\left({\delta }_B\right)}_1+{\left({\delta }_B\right)}_2\\ {\delta }_B=\frac{q{L}^4}{128E{I}_1}+\frac{15q{L}^4}{128E{I}_2}\\ {\delta }_B=\frac{q{L}^4}{128E{I}_1}\left[1+\frac{15I_1}{I_2}\right]\end{array}$

Conclusion:

The deflection ${\delta }_B$ is at the free end of beam is calculated due to load P using method of superposition.

To determine

The ratio r of the deflection ${\delta }_B$ to the deflection ${\delta }_1$ at the free end of a prismatic cantilever with the moment of inertia $I_1$ carrying the same load.

Answer to Problem 9.7.2P

The ratio r is $r=\frac{1}{16}\left[1+\frac{15I_1}{I_2}\right]$ of the deflection ${\delta }_B$ to the deflection ${\delta }_1$ at the free end of a prismatic cantilever with the moment of inertia $I_1$ carrying the same load.

Explanation of Solution

Given:

We have the data,

Length of the beam, L

Moment of inertia of, $AC=I_2$

Moment of inertia of, $BC=I_1$

Load at point B, P

  $AC=CB=\frac{L}{2}$

Concept Used:

The cantilever beam ACB as per the below figure supports a uniform load of intensity q throughout its length with moments of inertia $I_2{\text{ and I}}_1$ in parts of AC and CB.

  

Calculation:

For the prismatic cantilever beam, we have ${\delta }_1=\frac{q{L}^4}{8E{I}_1}$

We can calculate the ratio as below.

  $\begin{array}{l}r=\frac{{\delta }_B}{{\delta }_1}\\ r=\frac{\frac{q{L}^4}{128E{I}_1}\left[1+\frac{15I_1}{I_2}\right]}{\frac{q{L}^4}{8E{I}_1}}\\ r=\frac{1}{16}\left[1+\frac{15I_1}{I_2}\right]\end{array}$

Conclusion:

The ratio r is calculated using the cantilever beam concept and moment diagram.

To determine

To plot : A graph for the deflection ratio (r) versus the ratio $\frac{I_2}{I_1}$ moment of inertia.

Explanation of Solution

Given:

We have the data,

Length of the beam, L

Moment of inertia of, $AC=I_2$

Moment of inertia of, $BC=I_1$

Load at point B, P

  $AC=CB=\frac{L}{2}$

Concept Used:

The cantilever beam ACB as per the below figure supports a uniform load of intensity q throughout its length with moments of inertia $I_2{\text{ and I}}_1$ in parts of AC and CB.

  

Calculation:

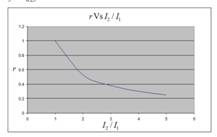
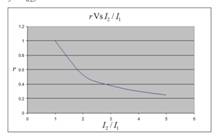
The values for plotting graph are shown in below table:

$\frac{I_2}{I_1}$	r
1	1
2	0.53
3	0.38
4	0.3
5	0.25

We will get graph as shown below:

  

Conclusion:

The graph for the deflection ratio (r) versus the ratio $\frac{I_2}{I_1}$ moment of inertia is as below: