FLUID MECHANICS FUNDAMENTALS+APPS
4th Edition
ISBN: 9781259877766
Author: CENGEL
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 9, Problem 34P
Imagine a steady, two-dimensional, incompressible flow that is purely radial in the xy-or-
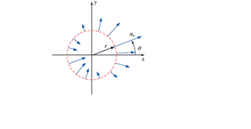
FIGURE P9-34
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A flow field is described in Cartesian coordinates by Is it incompressible?
V
u-v
Question 4: Consider fully developed Couette flow - flow between
two infinite parallel plates separated by distance h, with the top
plate moving and the bottom plate stationary as illustrated. The flow
is steady, incompressible, and two dimensional in the xy-plane. The
velocity field is given by V = (u,v) = (V y/h)ỉ + 0ỷ, Generate an
expression for stream function Yalong the vertical dashed line in
the figure. For convenience, 4= 0 along the bottom wall of the channel. What is the value of Y
along the top wall?
Consider fully developed Couette flow-flow between two infinite parallel plates separated by
distance h, with the top plate moving and the bottom plate stationary as illustrated in figure
below. The flow is steady, incompressible, and two-dimensional in the xy-plane. The velocity field
is given by:
V = (u, v) = V
+07
h
Is this flow rotational or irrotational? If it is rotational, calculate the vorticity component in the z-
direction. Do fluid particles in this flow rotate clockwise or counterclockwise?
u = v
Chapter 9 Solutions
FLUID MECHANICS FUNDAMENTALS+APPS
Ch. 9 - Explain the fundamental differences between a flow...Ch. 9 - What does it mean when we say that two more...Ch. 9 - The divergence theorem is v.cdv=A c . n dACh. 9 - Prob. 4CPCh. 9 - Prob. 5CPCh. 9 - Prob. 6CPCh. 9 - Prob. 7PCh. 9 - Prob. 8PCh. 9 - Let vector G=2xzi12x2jz2kk . Calculate the...Ch. 9 - Prob. 10P
Ch. 9 - Prob. 11PCh. 9 - Prob. 12PCh. 9 - Prob. 13PCh. 9 - Alex is measuring the time-averaged velocity...Ch. 9 - Let vector c be given G=4xziy2i+yzkand let V be...Ch. 9 - The product rule can be applied to the divergence...Ch. 9 - Prob. 18PCh. 9 - Prob. 19PCh. 9 - Prob. 20CPCh. 9 - In this chapter we derive the continuity equation...Ch. 9 - Repeat Example 9-1(gas compressed in a cylinder by...Ch. 9 - Consider the steady, two-dimensional velocity...Ch. 9 - The compressible from of the continuity equation...Ch. 9 - In Example 9-6 we derive the equation for...Ch. 9 - Consider a spiraling line vortex/sink flow in the...Ch. 9 - Verify that the steady; two-dimensional,...Ch. 9 - Consider steady flow of water through an...Ch. 9 - Consider the following steady, three-dimensional...Ch. 9 - Consider the following steady, three-dimensional...Ch. 9 - Two velocity components of a steady,...Ch. 9 - Imagine a steady, two-dimensional, incompressible...Ch. 9 - The u velocity component of a steady,...Ch. 9 - Imagine a steady, two-dimensional, incompressible...Ch. 9 - The u velocity component of a steady,...Ch. 9 - What is significant about curves of constant...Ch. 9 - In CFD lingo, the stream function is often called...Ch. 9 - Prob. 39CPCh. 9 - Prob. 40CPCh. 9 - Prob. 41PCh. 9 - Prob. 42PCh. 9 - Prob. 44PCh. 9 - Prob. 45PCh. 9 - As a follow-up to Prob. 9-45, calculate the volume...Ch. 9 - Consider the Couette flow of Fig.9-45. For the...Ch. 9 - Prob. 48PCh. 9 - AS a follow-up to Prob. 9-48, calculate the volume...Ch. 9 - Consider the channel flow of Fig. 9-45. The fluid...Ch. 9 - In the field of air pollution control, one often...Ch. 9 - Suppose the suction applied to the sampling...Ch. 9 - Prob. 53PCh. 9 - Flow separates at a shap corner along a wall and...Ch. 9 - Prob. 55PCh. 9 - Prob. 56PCh. 9 - Prob. 58PCh. 9 - Prob. 59PCh. 9 - Prob. 60PCh. 9 - Prob. 61PCh. 9 - Prob. 62PCh. 9 - Prob. 63EPCh. 9 - Prob. 64PCh. 9 - Prob. 65EPCh. 9 - Prob. 66PCh. 9 - Prob. 68EPCh. 9 - Prob. 69PCh. 9 - Prob. 71PCh. 9 - Prob. 72PCh. 9 - Prob. 73PCh. 9 - Prob. 74PCh. 9 - Prob. 75PCh. 9 - Wht in the main distionction between Newtormine...Ch. 9 - Prob. 77CPCh. 9 - What are constitutive equations, and to the fluid...Ch. 9 - An airplane flies at constant velocity Vairplane...Ch. 9 - Define or describe each type of fluid: (a)...Ch. 9 - The general cool volume from of linearmomentum...Ch. 9 - Consider the steady, two-dimensional,...Ch. 9 - Consider the following steady, two-dimensional,...Ch. 9 - Consider the following steady, two-dimensional,...Ch. 9 - Consider liquid in a cylindrical tank. Both the...Ch. 9 - Engine oil at T=60C is forced to flow between two...Ch. 9 - Consider steady, two-dimensional, incompressible...Ch. 9 - Consider steady, incompressible, parallel, laminar...Ch. 9 - Prob. 89PCh. 9 - Prob. 90PCh. 9 - Prob. 91PCh. 9 - The first viscous terms in -comonent of the...Ch. 9 - An incompressible Newtonian liquid is confined...Ch. 9 - Prob. 94PCh. 9 - Prob. 95PCh. 9 - Prob. 96PCh. 9 - Prob. 97PCh. 9 - Consider steady, incompressible, laminar flow of a...Ch. 9 - Consider again the pipe annulus sketched in Fig...Ch. 9 - Repeat Prob. 9-99 except swap the stationary and...Ch. 9 - Consider a modified form of Couette flow in which...Ch. 9 - Consider dimensionless velocity distribution in...Ch. 9 - Consider steady, incompressible, laminar flow of a...Ch. 9 - Prob. 104PCh. 9 - Prob. 105PCh. 9 - Prob. 106PCh. 9 - Prob. 107CPCh. 9 - Prob. 108CPCh. 9 - Discuss the relationship between volumetric strain...Ch. 9 - Prob. 110CPCh. 9 - Prob. 111CPCh. 9 - Prob. 112PCh. 9 - Prob. 113PCh. 9 - Look up the definition of Poisson’s equation in...Ch. 9 - Prob. 115PCh. 9 - Prob. 116PCh. 9 - Prob. 117PCh. 9 - For each of the listed equation, write down the...Ch. 9 - Prob. 119PCh. 9 - Prob. 120PCh. 9 - A block slides down along, straight inclined wall...Ch. 9 - Water flows down a long, straight, inclined pipe...Ch. 9 - Prob. 124PCh. 9 - Prob. 125PCh. 9 - Prob. 126PCh. 9 - Prob. 128PCh. 9 - The Navier-Stokes equation is also known as (a)...Ch. 9 - Which choice is not correct regarding the...Ch. 9 - In thud flow analyses, which boundary condition...Ch. 9 - Which choice is the genera1 differential equation...Ch. 9 - Which choice is the differential , incompressible,...Ch. 9 - A steady, two-dimensional, incompressible flow...Ch. 9 - A steady, two-dimensional, incompressible flow...Ch. 9 - A steady velocity field is given by...Ch. 9 - Prob. 137P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Pravin bhaiarrow_forwardPerform the convective on velocity vectors u in cylindrical coordinates : Du/Dtarrow_forwardConsider steady, two-dimensional, incompressible flow due to a spiraling line vortex/sink flow centered on the z-axis. Streamlines and velocity components are shown in Fig. The velocity field is ur = C/r and u? = K/r, where C and K are constants. Calculate the pressure as a function of r and ?.arrow_forward
- Consider fully developed Couette flow between two infinite parallel plates separated by distance h, with the top plate moving and the bottom plate stationary, as illustrated in the figure below. The flow is steady, incompressible, and two-dimensional in the XY plane. The velocity field is given by V }i = (u, v) = (v² )i +0j = V (a) Find out the acceleration field of this flow. (b) Is this flow steady? What are the u and v components of velocity? u= V² harrow_forwardAy j. Is this a possible case of incompres- 3.9 A velocity field is given by V= Axyi -- %3D sible flow? If yes, obtain the stream function and find the value of constant A for which the flow rate between the streamlines passing through the points (3, 3) and (3, 4) is 18 units. Axy Ans: V = 12 + C, A 7 2arrow_forwardConsider two-dimensional flow in the x-y plane where we are using polar coordinatesr and O to describe the motion. We will call u the radial velocity and v the azimuthal velocity (see figure below). y u Xarrow_forward
- A subtle point, often missed by students of fluid mechanics (and even their professors!), is that an inviscid region of flow is not the same as an irrotational (potential) region of flow. Discuss the differences and similarities between these two approximations. Give an example of each.arrow_forwardIn deriving the vorticity equation, we have used the identity divergence x (divergence P) = 0 Show that this identity is valid for any scalar lamda by checking it in Cartesian and cylindrical coordinates.arrow_forwardImagine a steady, two-dimensional, incompressible flow that is purely radial in the xy- or r?-plane. In other words, velocity component ur is nonzero, but u? is zero everywhere. What is the most general form of velocity component ur that does not violate conservation of mass?arrow_forward
- What is the streamline equation in Cartesian coordinates? Why does Bernoulli equation hold on a streamline for a rotational flow field?arrow_forwardhe velocity at apoint in aflued for one-dimensional Plow wmay be aiven in The Eutkerian coordinater by U=Ax+ Bt, Show That X Coordinates Canbe obtained from The Eulerian system. The intial position by Xo and The intial time to zo man be assumeal · 1. x = foxo, yo) in The Lagrange of The fluid parficle is designatedarrow_forwardThe velocity field for a line vortex in the r?-plane is given byur = 0 u? = K / rwhere K is the line vortex strength. For the case with K = 1.5 m/s2, plot a contour plot of velocity magnitude (speed). Specifically, draw curves of constant speed V = 0.5, 1.0, 1.5, 2.0, and 2.5 m/s. Be sure to label these speeds on your plot.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Introduction to Kinematics; Author: LearnChemE;https://www.youtube.com/watch?v=bV0XPz-mg2s;License: Standard youtube license