Chapter 8.4, Problem 20E

(a)

To determine

To sketch: the curve of the given parametric equation

Answer to Problem 20E

  

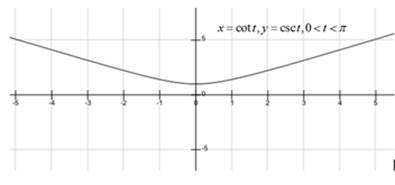
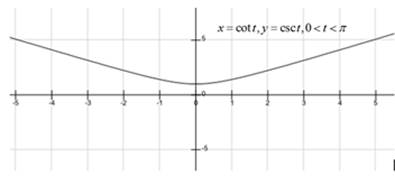
Explanation of Solution

Given: $x=\cot t,y=\csc t,0\le t<\pi$

Calculation:

Sketch the curve represented by the parametric equations

  $x=\cot t,y=\csc t,0\le t<\pi$.

For every value of $t$ , get a point on the curve.

If $t=\frac{\pi }{4}$ , then

  $\begin{array}{l}x=\cot \left(\frac{\pi }{4}\right)\\ \text{ =1,}\end{array}$

and

  $\begin{array}{l}y=\csc \left(\frac{\pi }{4}\right)\\ \text{ =}\sqrt{2}\text{,}\end{array}$

So the point corresponding to $t=\frac{\pi }{4}$is $\left(1,\sqrt{2}\right)$ .

The points $\left(x,y\right)$determined for different values of $t$ are shown in the following table.

$t$	$x$	$y$
$\frac{\pi }{4}$	$1$	$\sqrt{2}$
$\frac{\pi }{2}$	$0$	$1$
$\frac{3\pi }{4}$	$-1$	$\sqrt{2}$

Plotting these points get the following graph of the curve.

  

Conclusion:

Hence, the curve represented by the given parametric equation is sketched.

(b)

To determine

To find: the rectangular coordinate equation for the curve.

Answer to Problem 20E

Here, the given curve has the rectangular coordinate equation $y^2=1+x^2$ .

Explanation of Solution

Calculation:

find a rectangular-coordinate equation for the curve, represented by the parametric equations,

  $x=\cot t,y=\csc t,0\le t<\pi ,$

by eliminating the parameter.

To eliminate the parameter, use the trigonometric identity ${\csc }^{2}t=1+{\cot }^{2}t.$

From the given equations,

  $\cot t=x,$

and

  $\csc t=y.$

Substituting the values of $\cot t$ and $\csc t$ , in ${\csc }^{2}t=1+{\cot }^{2}t$ ,

  $y^2=1+x^2.$

Therefore, the given curve has the rectangular coordinate equation,

  $\boxed{y^2=1+x^2.}$

Conclusion:

Hence, the given curve has the rectangular coordinate equation $y^2=1+x^2$ .