
Concept explainers
(a)
To sketch: the curve of the given parametric equation
(a)
Answer to Problem 19E
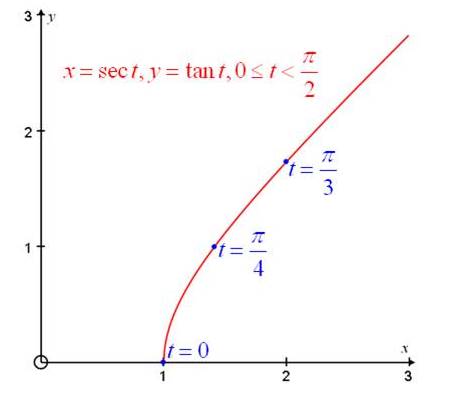
Explanation of Solution
Given:
Calculation:
Sketch the curve represented by the parametric equations
For every value of
If
and
So the point corresponding to
The points
Plotting these points get the following graph of the curve.
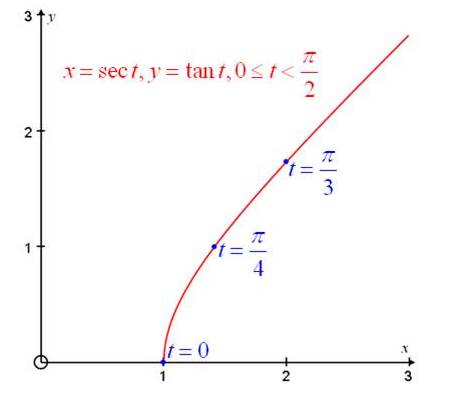
Conclusion:
Hence, the curve represented by the given parametric equation is sketched.
(b)
To find: the rectangular coordinate equation for the curve.
(b)
Answer to Problem 19E
Here, the given curve has the rectangular coordinate equation
Explanation of Solution
Calculation:
find a rectangular-coordinate equation for the curve, represented by the parametric equations,
by eliminating the parameter.
To eliminate the parameter, use the
From the given equations,
and
Substituting the values of
Therefore, the given curve has the rectangular coordinate equation,
Conclusion:
Hence, the given curve has the rectangular coordinate equation
Chapter 8 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





