Chapter 8.3, Problem 4E

How many different nth roots does a nonzero complex number have? __________. The number 16 has __________ fourth roots. These roots are __________, __________, __________, and __________. In the complex plane these roots all lie on a circle of radius __________. Graph the roots on the following graph.

To determine

Number of different roots of a non-zero complex number and the fourth root of 16 also the radius of the circle in the complex plane in which the all these roots lie and sketch the graph of all roots on the given axis.

Answer to Problem 4E

There are n Number of different roots of a non-zero complex number and the forth root of 16 is $2,2i,-2,-2i$ and these all roots lie in the circle of radius 4 on the complex plane.

Explanation of Solution

Section1:

Any complex number $z=r\left(\cos \theta +i\sin \theta \right)$ has exactly n different nth roots.

According to De Moiver’s Theorem.

$w_k=r^{\frac{1}{n}}\left[\cos \left(\frac{\theta +2k\pi }{n}\right)+i\sin \left(\frac{\theta +2k\pi }{n}\right)\right]$ (1)

Where, $k=0,1,2,3\cdots \left(n-1\right)$, r is modulus of z and $\theta$ is argument of z.

For fourth root of 156, of which there are exactly 4, 16 has a modulus $r=16$ and argument $\theta =0$ since it is a real line.

Substitute 16 for r, 4 for n, 0 for $\theta$ and 0 for k in equation (1) to calculate $w_0$.

$\begin{array}{c}{w}_0={16}^{\frac{1}{4}}\left[\cos \left(\frac{0+2\left(0\right)\pi }{4}\right)+i\sin \left(\frac{0+2\left(0\right)\pi }{4}\right)\right]\\ =2\left[\cos 0+i\sin 0\right]\\ =2\end{array}$

Substitute 16 for r, 4 for n, 0 for $\theta$ and 1 for k in equation (1) to calculate $w_1$.

$\begin{array}{c}{w}_0={16}^{\frac{1}{4}}\left[\cos \left(\frac{0+2\left(1\right)\pi }{4}\right)+i\sin \left(\frac{0+2\left(1\right)\pi }{4}\right)\right]\\ =2\left[\cos \left(\frac{2\pi }{4}\right)+i\sin \left(\frac{2\pi }{4}\right)\right]\\ =2\left[\cos \left(\frac{\pi }{2}\right)+i\sin \left(\frac{\pi }{2}\right)\right]\\ =2i\end{array}$

Substitute 16 for r, 4 for n, 0 for $\theta$ and 2 for k in equation (1) to calculate $w_1$.

$\begin{array}{c}{w}_0={16}^{\frac{1}{4}}\left[\cos \left(\frac{0+2\left(2\right)\pi }{4}\right)+i\sin \left(\frac{0+2\left(2\right)\pi }{4}\right)\right]\\ =2\left[\cos \left(\frac{4\pi }{4}\right)+i\sin \left(\frac{4\pi }{4}\right)\right]\\ =2\left[\cos \left(\pi \right)+i\sin \left(\pi \right)\right]\\ =-2\end{array}$

Substitute 16 for r, 4 for n, 0 for $\theta$ and 3 for k in equation (1) to calculate $w_0$.

$\begin{array}{c}{w}_0={16}^{\frac{1}{4}}\left[\cos \left(\frac{0+2\left(3\right)\pi }{4}\right)+i\sin \left(\frac{0+2\left(3\right)\pi }{4}\right)\right]\\ =2\left[\cos \left(\frac{6\pi }{4}\right)+i\sin \left(\frac{6\pi }{4}\right)\right]\\ =2\left[\cos \left(\frac{3\pi }{2}\right)+i\sin \left(\frac{3\pi }{2}\right)\right]\\ =-2i\end{array}$

So, the forth root of 16 is $2,2i,-2,-2i$

It can be observed that these all roots lie in the circle of radius 4 on the complex plane.

Therefore, there are n Number of different roots of a non-zero complex number and the fourth root of 16 is $2,2i,-2,-2i$ and these all roots lie in the circle of radius 4 on the complex plane.

Section2:

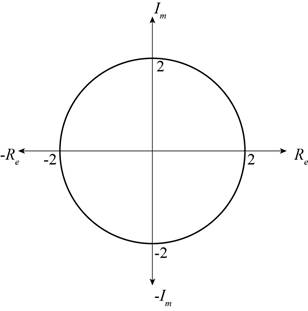
Figure (1)

Figure (1) shows the graph of all the fourth roots of 16 in the complex plane which lie in the circle of radius 4.