PRECALCULUS:GRAPHICAL,...-NASTA ED.
PRECALCULUS:GRAPHICAL,...-NASTA ED.
10th Edition
ISBN: 9780134672090
Author: Demana
Publisher: PEARSON
Expert Solution & Answer
Book Icon
Chapter 7, Problem 70RE
Solution

a.

To calculate: The linear regression models and superimpose its graph on a scatter plot of the data.

The obtained matrix is y≈28.92x+210.705 .

Given Information:

The table is defined,

    Time (years)Disbursements (billions of $)
    2005336.9
    2010521.2
    2011560.3
    2012550.1
    2013581.7
    2014600.3
    2015638.1

Calculation:

Consider the given table,

    Time (years)Disbursements (billions of $)
    2005336.9
    2010521.2
    2011560.3
    2012550.1
    2013581.7
    2014600.3
    2015638.1

Use a graphing calculator to find the linear rgeression.

Step 1. Insert the table in calculator by using the table feature.

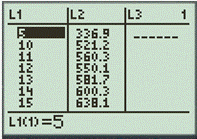
  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter 7, Problem 70RE , additional homework tip 1

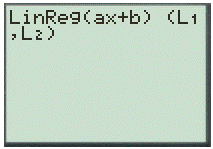
Step 2. Use the LinReg feature with first two list L1 and L2 o obtain the linear regression model for the population of Philadelphia.

  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter 7, Problem 70RE , additional homework tip 2

And,

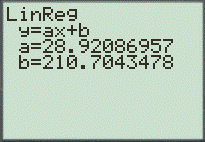
  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter 7, Problem 70RE , additional homework tip 3

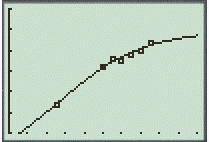
Step 3. Use the Graph feature to plot the both the graph as scatter graph.

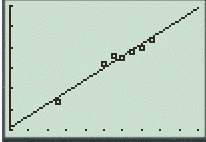
  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter 7, Problem 70RE , additional homework tip 4

Therefore, the obtained equation is y≈28.92x+210.705 .

b.

To calculate: The logistic regression model and superimpose its graph on a scatter plot of the data.

The obtained model is y≈695.751+3.178e−0.221x .

Given Information:

The table is defined,

    Time (years)Disbursements (billions of $)
    2005336.9
    2010521.2
    2011560.3
    2012550.1
    2013581.7
    2014600.3
    2015638.1

Calculation:

Consider the given table,

    Time (years)Disbursements (billions of $)
    2005336.9
    2010521.2
    2011560.3
    2012550.1
    2013581.7
    2014600.3
    2015638.1

Use a graphing calculator to find the logestic model.

Step 1. Insert the table in calculator by using the table feature.

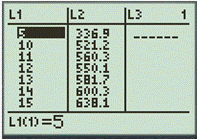
  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter 7, Problem 70RE , additional homework tip 5

Step 2. Use the LinReg feature with first two list L1 and L2 o obtain the linear regression model for the population of Philadelphia.

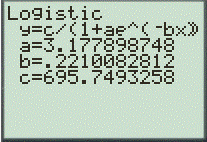
  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter 7, Problem 70RE , additional homework tip 6

Step 3. Use the Graph feature to plot the both the graph as scatter graph.

  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter 7, Problem 70RE , additional homework tip 7

Hence, the obtained result is y≈695.751+3.178e−0.221x .

c.

To determine: The models in parts (a) and (b) predict the same disbursement amounts.

The obtained model is y≈695.751+3.178e−0.221x .

Given Information:

The table is defined,

    Time (years)Disbursements (billions of $)
    2005336.9
    2010521.2
    2011560.3
    2012550.1
    2013581.7
    2014600.3
    2015638.1

Calculation:

Consider the given table,

    Time (years)Disbursements (billions of $)
    2005336.9
    2010521.2
    2011560.3
    2012550.1
    2013581.7
    2014600.3
    2015638.1

Use a graphing calculator to find the logestic model.

Step 1. Insert the table in calculator by using the table feature.

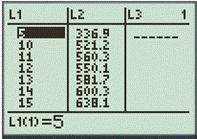
  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter 7, Problem 70RE , additional homework tip 8

Step 2. Graph the both equations (a) and (b) then use the intersect feature to find the intersection point.

  PRECALCULUS:GRAPHICAL,...-NASTA ED., Chapter 7, Problem 70RE , additional homework tip 9

The  x -coordinates are about 6.8 and 13.3, representing the years 2006 and 2013, respectively.

Hence, the obtained years are 2006 and 2013.

d.

To determine: The models, which appears to be a better fit for the data and explain which model would you choose to make predictions beyond 2020

The first choice is logistic model and then linear model.

Given Information:

The table is defined,

    Time (years)Disbursements (billions of $)
    2005336.9
    2010521.2
    2011560.3
    2012550.1
    2013581.7
    2014600.3
    2015638.1

Calculation:

Consider the given information,

The logistic model seems to be a better fit for the data since it passes most points compared to the linear model. For predictions beyond 2020, I would choose the linear model because the trend of the disbursement appears to be increasing.

The logistic model has a limiting growth of about 696 billion dollars which does not make sense in real life.

Hence, the first choice is logistic model and then linear model.

Previous
Chapter 7, Problem 69RE
Next
Chapter 7, Problem 71RE

Chapter 7 Solutions

PRECALCULUS:GRAPHICAL,...-NASTA ED.

Ch. 7.1 - Prob. 1QRCh. 7.1 - Prob. 2QRCh. 7.1 - Prob. 3QRCh. 7.1 - Prob. 4QRCh. 7.1 - Prob. 5QRCh. 7.1 - Prob. 6QRCh. 7.1 - Prob. 7QRCh. 7.1 - Prob. 8QRCh. 7.1 - Prob. 9QRCh. 7.1 - Prob. 10QR
Ch. 7.1 - Prob. 1ECh. 7.1 - Prob. 2ECh. 7.1 - Prob. 3ECh. 7.1 - Prob. 4ECh. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Prob. 7ECh. 7.1 - Prob. 8ECh. 7.1 - Prob. 9ECh. 7.1 - Prob. 10ECh. 7.1 - Prob. 11ECh. 7.1 - Prob. 12ECh. 7.1 - Prob. 13ECh. 7.1 - Prob. 14ECh. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Prob. 18ECh. 7.1 - Prob. 19ECh. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Prob. 39ECh. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.1 - Prob. 45ECh. 7.1 - Prob. 46ECh. 7.1 - Prob. 47ECh. 7.1 - Prob. 48ECh. 7.1 - Prob. 49ECh. 7.1 - Prob. 50ECh. 7.1 - Prob. 51ECh. 7.1 - Prob. 52ECh. 7.1 - Prob. 53ECh. 7.1 - Prob. 54ECh. 7.1 - Prob. 55ECh. 7.1 - Prob. 56ECh. 7.1 - Prob. 57ECh. 7.1 - Prob. 58ECh. 7.1 - Prob. 59ECh. 7.1 - Prob. 60ECh. 7.1 - Prob. 61ECh. 7.1 - Prob. 62ECh. 7.1 - Prob. 63ECh. 7.1 - Prob. 64ECh. 7.1 - Prob. 65ECh. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Prob. 69ECh. 7.1 - Prob. 70ECh. 7.2 - Prob. 1QRCh. 7.2 - Prob. 2QRCh. 7.2 - Prob. 3QRCh. 7.2 - Prob. 4QRCh. 7.2 - Prob. 5QRCh. 7.2 - Prob. 6QRCh. 7.2 - Prob. 7QRCh. 7.2 - Prob. 8QRCh. 7.2 - Prob. 9QRCh. 7.2 - Prob. 10QRCh. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - Prob. 4ECh. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Prob. 7ECh. 7.2 - Prob. 8ECh. 7.2 - Prob. 9ECh. 7.2 - Prob. 10ECh. 7.2 - Prob. 11ECh. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Prob. 14ECh. 7.2 - Prob. 15ECh. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Prob. 19ECh. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Prob. 22ECh. 7.2 - Prob. 23ECh. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Prob. 26ECh. 7.2 - Prob. 27ECh. 7.2 - Prob. 28ECh. 7.2 - Prob. 29ECh. 7.2 - Prob. 30ECh. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Prob. 34ECh. 7.2 - Prob. 35ECh. 7.2 - Prob. 36ECh. 7.2 - Prob. 37ECh. 7.2 - Prob. 38ECh. 7.2 - Prob. 39ECh. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.2 - Prob. 45ECh. 7.2 - Prob. 46ECh. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Prob. 49ECh. 7.2 - Prob. 50ECh. 7.2 - Prob. 51ECh. 7.2 - Prob. 52ECh. 7.2 - Prob. 53ECh. 7.2 - Prob. 54ECh. 7.2 - Prob. 55ECh. 7.2 - Prob. 56ECh. 7.2 - Prob. 57ECh. 7.2 - Prob. 58ECh. 7.2 - Prob. 59ECh. 7.2 - Prob. 60ECh. 7.2 - Prob. 61ECh. 7.2 - Prob. 62ECh. 7.2 - Prob. 63ECh. 7.2 - Prob. 64ECh. 7.2 - Prob. 65ECh. 7.2 - Prob. 66ECh. 7.2 - Prob. 67ECh. 7.2 - Prob. 68ECh. 7.2 - Prob. 69ECh. 7.2 - Prob. 70ECh. 7.2 - Prob. 71ECh. 7.2 - Prob. 72ECh. 7.2 - Prob. 73ECh. 7.3 - Prob. 1QRCh. 7.3 - Prob. 2QRCh. 7.3 - Prob. 3QRCh. 7.3 - Prob. 4QRCh. 7.3 - Prob. 5QRCh. 7.3 - Prob. 6QRCh. 7.3 - Prob. 7QRCh. 7.3 - Prob. 8QRCh. 7.3 - Prob. 9QRCh. 7.3 - Prob. 10QRCh. 7.3 - Prob. 1ECh. 7.3 - Prob. 2ECh. 7.3 - Prob. 3ECh. 7.3 - Prob. 4ECh. 7.3 - Prob. 5ECh. 7.3 - Prob. 6ECh. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Prob. 9ECh. 7.3 - Prob. 10ECh. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Prob. 13ECh. 7.3 - Prob. 14ECh. 7.3 - Prob. 15ECh. 7.3 - Prob. 16ECh. 7.3 - Prob. 17ECh. 7.3 - Prob. 18ECh. 7.3 - Prob. 19ECh. 7.3 - Prob. 20ECh. 7.3 - Prob. 21ECh. 7.3 - Prob. 22ECh. 7.3 - Prob. 23ECh. 7.3 - Prob. 24ECh. 7.3 - Prob. 25ECh. 7.3 - Prob. 26ECh. 7.3 - Prob. 27ECh. 7.3 - Prob. 28ECh. 7.3 - Prob. 29ECh. 7.3 - Prob. 30ECh. 7.3 - Prob. 31ECh. 7.3 - Prob. 32ECh. 7.3 - Prob. 33ECh. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Prob. 36ECh. 7.3 - Prob. 37ECh. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - Prob. 40ECh. 7.3 - Prob. 41ECh. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - Prob. 45ECh. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - Prob. 48ECh. 7.3 - Prob. 49ECh. 7.3 - Prob. 50ECh. 7.3 - Prob. 51ECh. 7.3 - Prob. 52ECh. 7.3 - Prob. 53ECh. 7.3 - Prob. 54ECh. 7.3 - Prob. 55ECh. 7.3 - Prob. 56ECh. 7.3 - Prob. 57ECh. 7.3 - Prob. 58ECh. 7.3 - Prob. 59ECh. 7.3 - Prob. 60ECh. 7.3 - Prob. 61ECh. 7.3 - Prob. 62ECh. 7.3 - Prob. 63ECh. 7.3 - Prob. 64ECh. 7.3 - Prob. 65ECh. 7.3 - Prob. 66ECh. 7.3 - Prob. 67ECh. 7.3 - Prob. 68ECh. 7.3 - Prob. 69ECh. 7.3 - Prob. 70ECh. 7.3 - Prob. 71ECh. 7.3 - Prob. 72ECh. 7.3 - Prob. 73ECh. 7.3 - Prob. 74ECh. 7.3 - Prob. 75ECh. 7.3 - Prob. 76ECh. 7.3 - Prob. 77ECh. 7.3 - Prob. 78ECh. 7.3 - Prob. 79ECh. 7.3 - Prob. 80ECh. 7.3 - Prob. 81ECh. 7.3 - Prob. 82ECh. 7.3 - Prob. 83ECh. 7.3 - Prob. 84ECh. 7.3 - Prob. 85ECh. 7.3 - Prob. 86ECh. 7.3 - Prob. 87ECh. 7.3 - Prob. 88ECh. 7.3 - Prob. 89ECh. 7.3 - Prob. 90ECh. 7.3 - Prob. 91ECh. 7.3 - Prob. 92ECh. 7.3 - Prob. 93ECh. 7.3 - Prob. 94ECh. 7.3 - Prob. 95ECh. 7.3 - Prob. 96ECh. 7.3 - Prob. 97ECh. 7.3 - Prob. 98ECh. 7.3 - Prob. 99ECh. 7.3 - Prob. 100ECh. 7.3 - Prob. 101ECh. 7.3 - Prob. 102ECh. 7.3 - Prob. 103ECh. 7.3 - Prob. 104ECh. 7.3 - Prob. 105ECh. 7.3 - Prob. 106ECh. 7.3 - Prob. 107ECh. 7.3 - Prob. 108ECh. 7.3 - Prob. 109ECh. 7.3 - Prob. 110ECh. 7.4 - Prob. 1QRCh. 7.4 - Prob. 2QRCh. 7.4 - Prob. 3QRCh. 7.4 - Prob. 4QRCh. 7.4 - Prob. 5QRCh. 7.4 - Prob. 6QRCh. 7.4 - Prob. 7QRCh. 7.4 - Prob. 8QRCh. 7.4 - Prob. 9QRCh. 7.4 - Prob. 10QRCh. 7.4 - Prob. 1ECh. 7.4 - Prob. 2ECh. 7.4 - Prob. 3ECh. 7.4 - Prob. 4ECh. 7.4 - Prob. 5ECh. 7.4 - Prob. 6ECh. 7.4 - Prob. 7ECh. 7.4 - Prob. 8ECh. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Prob. 11ECh. 7.4 - Prob. 12ECh. 7.4 - Prob. 13ECh. 7.4 - Prob. 14ECh. 7.4 - Prob. 15ECh. 7.4 - Prob. 16ECh. 7.4 - Prob. 17ECh. 7.4 - Prob. 18ECh. 7.4 - Prob. 19ECh. 7.4 - Prob. 20ECh. 7.4 - Prob. 21ECh. 7.4 - Prob. 22ECh. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - Prob. 30ECh. 7.4 - Prob. 31ECh. 7.4 - Prob. 32ECh. 7.4 - Prob. 33ECh. 7.4 - Prob. 34ECh. 7.4 - Prob. 35ECh. 7.4 - Prob. 36ECh. 7.4 - Prob. 37ECh. 7.4 - Prob. 38ECh. 7.4 - Prob. 39ECh. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Prob. 44ECh. 7.4 - Prob. 45ECh. 7.4 - Prob. 46ECh. 7.4 - Prob. 47ECh. 7.4 - Prob. 48ECh. 7.4 - Prob. 49ECh. 7.4 - Prob. 50ECh. 7.4 - Prob. 51ECh. 7.4 - Prob. 52ECh. 7 - Prob. 1RECh. 7 - Prob. 2RECh. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - Prob. 14RECh. 7 - Prob. 15RECh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Prob. 19RECh. 7 - Prob. 20RECh. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - Prob. 34RECh. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Prob. 44RECh. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Prob. 51RECh. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 54RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - Prob. 62RECh. 7 - Prob. 63RECh. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 69RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - Prob. 75RECh. 7 - Prob. 76RECh. 7 - Prob. 77RECh. 7 - Prob. 78RECh. 7 - Prob. 79RECh. 7 - Prob. 80RECh. 7 - Prob. 81RE
Knowledge Booster
Background pattern image
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS