Chapter 6.3, Problem 14E

Solution

To find: the probability that a randomly selected x-value from the distribution is in the given interval

  $P\left(x\ge 25\right)=0.975$

Given information:

The given interval is: at least 25

A normal distribution has a mean of 33 and a standard deviation of 4.

Concept Used:

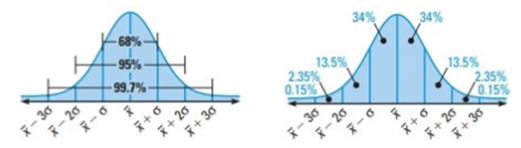
Areas under a Normal Curve

A normal distribution with mean $\overline{x}$ and standard deviation $\sigma$ has the following properties:

• The total area under the related normal curve is 1.
• About 68% of the area lies within 1 standard deviation of the mean.
• About 95% of the area lies within 2 standard deviation of the mean.
• About 99.7% of the area lies within 3 standard deviation of the mean.

  

Explanation:

The normal distribution curve for the given distribution with mean $\overline{x}=33$ and standard deviation $\sigma =4$ is:

  

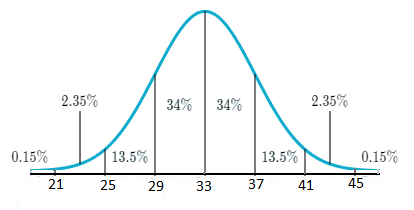
The required interval of at least 25 represents the shaded area under the normal curve (it is the area lies after $\overline{x}-2\sigma$ ) as shown below:

  

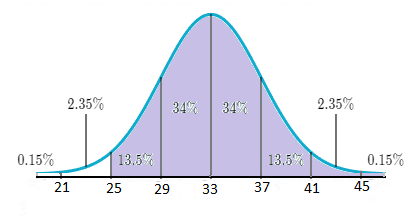
So, the probability that a randomly selected x-value from the distribution is in the given interval is:

  $\begin{array}{c}P\left(x\ge 25\right)=0.135+0.34+0.34+0.135+0.0235+0.0015\\ =0.975\end{array}$