Precalculus: Mathematics for Calculus - 6th Edition

6th Edition

ISBN: 9780840068071

Author: Stewart, James, Redlin, Lothar, Watson, Saleem

Publisher: Cengage Learning

See similar textbooks

Videos

Question

Chapter 5, Problem 56RE

(a)

To determine

To find: TheGraphing device to graph the function.

(a)

Expert Solution

Answer to Problem 56RE

The function has $Domain=(−∞,∞)$ and $Range=[1.5, 3]$ .

Explanation of Solution

Given: $y=1+2cosx$

Concept used:

$Cosx$ is even function over all equation change to $even$ .

Its $Domain=(−∞,∞)$ and $Range=[1.5, 3]$ .

Amplitude is $A=(3−1.5)=1.5$

Calculation:

Thee graph of the $y=1+2cosx$ .

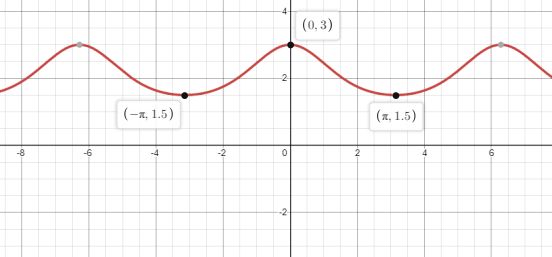
Precalculus: Mathematics for Calculus - 6th Edition, Chapter 5, Problem 56RE

Graphing device use here is Desmos graphing calculator. from the graph modulus symbolize the positivity of the function which is shown in the graph.

Through graph range and domain can Measured which is

$Domain=(−∞,∞)$ and $Range=[1.5, 3]$ .

Hence the function has $Domain=(−∞,∞)$ and $Range=[1.5, 3]$ .

(b)

To determine

To find:whether the Function is periodic if then described it.

(b)

Expert Solution

Answer to Problem 56RE

The period here is $2π$ .

Explanation of Solution

Given: $y=1+2cosx$

Concept used:

Period is measured as distance it takes for the entire graph to repeat.

Since the period of the Cosine function is $π$ .

Calculation:

$y=1+2cosx$

Form the graph its clearly verified the periods as:

$Periods=π−(−π)=2π.$

Hence the period here is $2π$ .

(c)

To determine

To find: The graph whether the function is even or odd.

(c)

Expert Solution

Answer to Problem 56RE

The given function is even.

Explanation of Solution

Given: $y=1+2cosx$

Concept used:

$f(-x)=f(x)$ the function is an even function.

$f(-x)=-f(x)$ the function is and odd function

Calculation:

$y=1+2cosx$

Since $Cosx$ even functions and overall becomes even function so, the function is even function.

$f(-x)=1+2cos(-x)=1+2cosx=f(x)∀x.$

It looks like infinitely many arches of length $π$ and of height 1 in the upper half plane touching the x-axis and symmetrical about y-axis. Therefore, the function takes the same value at points on the x-axis which are equidistant form the y-axis.

Hence the given function is even.

Chapter 5, Problem 55RE

Chapter 5, Problem 57RE

Chapter 5 Solutions

Precalculus: Mathematics for Calculus - 6th Edition

Ch. 5.1 - Prob. 1E Ch. 5.1 - Prob. 2E Ch. 5.1 - Prob. 3E Ch. 5.1 - Prob. 4E Ch. 5.1 - Prob. 5E Ch. 5.1 - Prob. 6E Ch. 5.1 - Prob. 7E Ch. 5.1 - Prob. 8E Ch. 5.1 - Prob. 9E Ch. 5.1 - Prob. 10E

Ch. 5.1 - Prob. 11E Ch. 5.1 - Prob. 12E Ch. 5.1 - Prob. 13E Ch. 5.1 - Prob. 14E Ch. 5.1 - Prob. 15E Ch. 5.1 - Prob. 16E Ch. 5.1 - Prob. 17E Ch. 5.1 - Prob. 18E Ch. 5.1 - Prob. 19E Ch. 5.1 - Prob. 20E Ch. 5.1 - Prob. 21E Ch. 5.1 - Prob. 22E Ch. 5.1 - Prob. 23E Ch. 5.1 - Prob. 24E Ch. 5.1 - Prob. 25E Ch. 5.1 - Prob. 26E Ch. 5.1 - Prob. 27E Ch. 5.1 - Prob. 28E Ch. 5.1 - Prob. 29E Ch. 5.1 - Prob. 30E Ch. 5.1 - Prob. 31E Ch. 5.1 - Prob. 32E Ch. 5.1 - Prob. 33E Ch. 5.1 - Prob. 34E Ch. 5.1 - Prob. 35E Ch. 5.1 - Prob. 36E Ch. 5.1 - Prob. 37E Ch. 5.1 - Prob. 38E Ch. 5.1 - Prob. 39E Ch. 5.1 - Prob. 40E Ch. 5.1 - Prob. 41E Ch. 5.1 - Prob. 42E Ch. 5.1 - Prob. 43E Ch. 5.1 - Prob. 44E Ch. 5.1 - Prob. 45E Ch. 5.1 - Prob. 46E Ch. 5.1 - Prob. 47E Ch. 5.1 - Prob. 48E Ch. 5.1 - Prob. 49E Ch. 5.1 - Prob. 50E Ch. 5.1 - Prob. 51E Ch. 5.1 - Prob. 52E Ch. 5.1 - Prob. 53E Ch. 5.1 - Prob. 54E Ch. 5.1 - Prob. 55E Ch. 5.1 - Prob. 56E Ch. 5.1 - Prob. 57E Ch. 5.1 - Prob. 58E Ch. 5.2 - Let P(x, y) be the terminal point on the unit...Ch. 5.2 - If P(x, y) is on the unit circle, then x2 + y2 =...Ch. 5.2 - Prob. 3E Ch. 5.2 - Prob. 4E Ch. 5.2 - Prob. 5E Ch. 5.2 - Prob. 6E Ch. 5.2 - Prob. 7E Ch. 5.2 - Prob. 8E Ch. 5.2 - Prob. 9E Ch. 5.2 - Prob. 10E Ch. 5.2 - Prob. 11E Ch. 5.2 - Prob. 12E Ch. 5.2 - Prob. 13E Ch. 5.2 - Prob. 14E Ch. 5.2 - Prob. 15E Ch. 5.2 - Prob. 16E Ch. 5.2 - Prob. 17E Ch. 5.2 - Prob. 18E Ch. 5.2 - Prob. 19E Ch. 5.2 - Prob. 20E Ch. 5.2 - Prob. 21E Ch. 5.2 - Prob. 22E Ch. 5.2 - Prob. 23E Ch. 5.2 - Prob. 24E Ch. 5.2 - Prob. 25E Ch. 5.2 - Prob. 26E Ch. 5.2 - Prob. 27E Ch. 5.2 - Prob. 28E Ch. 5.2 - Prob. 29E Ch. 5.2 - Prob. 30E Ch. 5.2 - Prob. 31E Ch. 5.2 - Prob. 32E Ch. 5.2 - Prob. 33E Ch. 5.2 - Prob. 34E Ch. 5.2 - Prob. 35E Ch. 5.2 - Prob. 36E Ch. 5.2 - Prob. 37E Ch. 5.2 - Prob. 38E Ch. 5.2 - Prob. 39E Ch. 5.2 - Prob. 40E Ch. 5.2 - Prob. 41E Ch. 5.2 - Prob. 42E Ch. 5.2 - Prob. 43E Ch. 5.2 - Prob. 44E Ch. 5.2 - Prob. 45E Ch. 5.2 - Prob. 46E Ch. 5.2 - Prob. 47E Ch. 5.2 - Prob. 48E Ch. 5.2 - Prob. 49E Ch. 5.2 - Prob. 50E Ch. 5.2 - Prob. 51E Ch. 5.2 - Prob. 52E Ch. 5.2 - Prob. 53E Ch. 5.2 - Prob. 54E Ch. 5.2 - Prob. 55E Ch. 5.2 - Prob. 56E Ch. 5.2 - Prob. 57E Ch. 5.2 - Prob. 58E Ch. 5.2 - Prob. 59E Ch. 5.2 - Prob. 60E Ch. 5.2 - Prob. 61E Ch. 5.2 - Prob. 62E Ch. 5.2 - Prob. 63E Ch. 5.2 - Prob. 64E Ch. 5.2 - Prob. 65E Ch. 5.2 - Prob. 66E Ch. 5.2 - Prob. 67E Ch. 5.2 - Prob. 68E Ch. 5.2 - Prob. 69E Ch. 5.2 - Prob. 70E Ch. 5.2 - Prob. 71E Ch. 5.2 - Prob. 72E Ch. 5.2 - Prob. 73E Ch. 5.2 - Prob. 74E Ch. 5.2 - Prob. 75E Ch. 5.2 - Prob. 76E Ch. 5.2 - Prob. 77E Ch. 5.2 - Prob. 78E Ch. 5.2 - Prob. 79E Ch. 5.2 - Prob. 80E Ch. 5.2 - Prob. 81E Ch. 5.2 - Circadian Rhythms Everybodys blood pressure varies...Ch. 5.2 - Electric Circuit After the switch is closed in the...Ch. 5.2 - Bungee Jumping A bungee jumper plummets from a...Ch. 5.2 - Prob. 85E Ch. 5.2 - Prob. 86E Ch. 5.3 - Prob. 1E Ch. 5.3 - Prob. 2E Ch. 5.3 - Prob. 3E Ch. 5.3 - Prob. 4E Ch. 5.3 - Prob. 5E Ch. 5.3 - Prob. 6E Ch. 5.3 - Prob. 7E Ch. 5.3 - Prob. 8E Ch. 5.3 - Prob. 9E Ch. 5.3 - Prob. 10E Ch. 5.3 - Prob. 11E Ch. 5.3 - Prob. 12E Ch. 5.3 - Prob. 13E Ch. 5.3 - Prob. 14E Ch. 5.3 - Prob. 15E Ch. 5.3 - Prob. 16E Ch. 5.3 - Prob. 17E Ch. 5.3 - Prob. 18E Ch. 5.3 - Prob. 19E Ch. 5.3 - Prob. 20E Ch. 5.3 - Prob. 21E Ch. 5.3 - Prob. 22E Ch. 5.3 - Prob. 23E Ch. 5.3 - Prob. 24E Ch. 5.3 - Prob. 25E Ch. 5.3 - Prob. 26E Ch. 5.3 - Prob. 27E Ch. 5.3 - Prob. 28E Ch. 5.3 - Prob. 29E Ch. 5.3 - Prob. 30E Ch. 5.3 - Prob. 31E Ch. 5.3 - Prob. 32E Ch. 5.3 - Prob. 33E Ch. 5.3 - Prob. 34E Ch. 5.3 - Prob. 35E Ch. 5.3 - Prob. 36E Ch. 5.3 - Prob. 37E Ch. 5.3 - Prob. 38E Ch. 5.3 - Prob. 39E Ch. 5.3 - Prob. 40E Ch. 5.3 - Prob. 41E Ch. 5.3 - Prob. 42E Ch. 5.3 - Prob. 43E Ch. 5.3 - Prob. 44E Ch. 5.3 - Prob. 45E Ch. 5.3 - Prob. 46E Ch. 5.3 - Prob. 47E Ch. 5.3 - Prob. 48E Ch. 5.3 - Prob. 49E Ch. 5.3 - Prob. 50E Ch. 5.3 - Prob. 51E Ch. 5.3 - Prob. 52E Ch. 5.3 - Prob. 53E Ch. 5.3 - Prob. 54E Ch. 5.3 - Prob. 55E Ch. 5.3 - Prob. 56E Ch. 5.3 - Prob. 57E Ch. 5.3 - Prob. 58E Ch. 5.3 - Prob. 59E Ch. 5.3 - Prob. 60E Ch. 5.3 - Prob. 61E Ch. 5.3 - Prob. 62E Ch. 5.3 - Prob. 63E Ch. 5.3 - Prob. 64E Ch. 5.3 - Prob. 65E Ch. 5.3 - Prob. 66E Ch. 5.3 - Prob. 67E Ch. 5.3 - Prob. 68E Ch. 5.3 - Prob. 69E Ch. 5.3 - Prob. 70E Ch. 5.3 - Prob. 71E Ch. 5.3 - Prob. 72E Ch. 5.3 - Prob. 73E Ch. 5.3 - Prob. 74E Ch. 5.3 - Prob. 75E Ch. 5.3 - Prob. 76E Ch. 5.3 - Height of a Wave As a wave passes by an offshore...Ch. 5.3 - Sound Vibrations A tuning fork is struck,...Ch. 5.3 - Blood Pressure Each time your heart beats, your...Ch. 5.3 - Variable Stars Variable stars are ones whose...Ch. 5.3 - Prob. 81E Ch. 5.3 - Prob. 82E Ch. 5.3 - Prob. 83E Ch. 5.3 - Prob. 84E Ch. 5.4 - The trigonometric function y = tan x has period...Ch. 5.4 - The trigonometric function y = csc x has period...Ch. 5.4 - Prob. 3E Ch. 5.4 - Prob. 4E Ch. 5.4 - Prob. 5E Ch. 5.4 - Prob. 6E Ch. 5.4 - Prob. 7E Ch. 5.4 - Prob. 8E Ch. 5.4 - Prob. 9E Ch. 5.4 - Prob. 10E Ch. 5.4 - Prob. 11E Ch. 5.4 - Prob. 12E Ch. 5.4 - Prob. 13E Ch. 5.4 - Prob. 14E Ch. 5.4 - Prob. 15E Ch. 5.4 - Prob. 16E Ch. 5.4 - Prob. 17E Ch. 5.4 - Prob. 18E Ch. 5.4 - Prob. 19E Ch. 5.4 - Prob. 20E Ch. 5.4 - Prob. 21E Ch. 5.4 - Prob. 22E Ch. 5.4 - Prob. 23E Ch. 5.4 - Prob. 24E Ch. 5.4 - Prob. 25E Ch. 5.4 - Prob. 26E Ch. 5.4 - Prob. 27E Ch. 5.4 - Prob. 28E Ch. 5.4 - Prob. 29E Ch. 5.4 - Prob. 30E Ch. 5.4 - Prob. 31E Ch. 5.4 - Prob. 32E Ch. 5.4 - Prob. 33E Ch. 5.4 - Prob. 34E Ch. 5.4 - Prob. 35E Ch. 5.4 - Prob. 36E Ch. 5.4 - Prob. 37E Ch. 5.4 - Prob. 38E Ch. 5.4 - Prob. 39E Ch. 5.4 - Prob. 40E Ch. 5.4 - Prob. 41E Ch. 5.4 - Prob. 42E Ch. 5.4 - Prob. 43E Ch. 5.4 - Prob. 44E Ch. 5.4 - Prob. 45E Ch. 5.4 - Prob. 46E Ch. 5.4 - Prob. 47E Ch. 5.4 - Prob. 48E Ch. 5.4 - Prob. 49E Ch. 5.4 - Prob. 50E Ch. 5.4 - Prob. 51E Ch. 5.4 - Prob. 52E Ch. 5.4 - Prob. 53E Ch. 5.4 - Prob. 54E Ch. 5.4 - Prob. 55E Ch. 5.4 - Prob. 56E Ch. 5.4 - Lighthouse The beam from a lighthouse completes...Ch. 5.4 - Length of a Shadow On a day when the sun passes...Ch. 5.4 - Prob. 59E Ch. 5.5 - (a) To define the inverse sine function, we...Ch. 5.5 - The cancellation property sin1(sin x) = x is valid...Ch. 5.5 - Prob. 3E Ch. 5.5 - Prob. 4E Ch. 5.5 - Prob. 5E Ch. 5.5 - Prob. 6E Ch. 5.5 - Prob. 7E Ch. 5.5 - Prob. 8E Ch. 5.5 - Prob. 9E Ch. 5.5 - Prob. 10E Ch. 5.5 - Prob. 11E Ch. 5.5 - Prob. 12E Ch. 5.5 - Prob. 13E Ch. 5.5 - Prob. 14E Ch. 5.5 - Prob. 15E Ch. 5.5 - Prob. 16E Ch. 5.5 - Prob. 17E Ch. 5.5 - Prob. 18E Ch. 5.5 - Prob. 19E Ch. 5.5 - Prob. 20E Ch. 5.5 - Prob. 21E Ch. 5.5 - Prob. 22E Ch. 5.5 - Prob. 23E Ch. 5.5 - Prob. 24E Ch. 5.5 - Prob. 25E Ch. 5.5 - Prob. 26E Ch. 5.5 - Prob. 27E Ch. 5.5 - Prob. 28E Ch. 5.5 - Prob. 29E Ch. 5.5 - Prob. 30E Ch. 5.5 - Prob. 31E Ch. 5.5 - Prob. 32E Ch. 5.5 - Prob. 33E Ch. 5.5 - Prob. 34E Ch. 5.5 - Prob. 35E Ch. 5.5 - Prob. 36E Ch. 5.5 - Prob. 37E Ch. 5.5 - Prob. 38E Ch. 5.5 - Prob. 39E Ch. 5.5 - Prob. 40E Ch. 5.5 - Prob. 41E Ch. 5.5 - Prob. 42E Ch. 5.5 - Prob. 43E Ch. 5.5 - Prob. 44E Ch. 5.5 - Prob. 45E Ch. 5.5 - Prob. 46E Ch. 5.5 - Prob. 47E Ch. 5.6 - For an object in simple harmonic motion with...Ch. 5.6 - For an object in damped harmonic motion with...Ch. 5.6 - Prob. 3E Ch. 5.6 - Prob. 4E Ch. 5.6 - Prob. 5E Ch. 5.6 - Prob. 6E Ch. 5.6 - Prob. 7E Ch. 5.6 - Prob. 8E Ch. 5.6 - Prob. 9E Ch. 5.6 - Prob. 10E Ch. 5.6 - Prob. 11E Ch. 5.6 - Prob. 12E Ch. 5.6 - Prob. 13E Ch. 5.6 - Prob. 14E Ch. 5.6 - Prob. 15E Ch. 5.6 - Prob. 16E Ch. 5.6 - Prob. 17E Ch. 5.6 - Prob. 18E Ch. 5.6 - Prob. 19E Ch. 5.6 - Prob. 20E Ch. 5.6 - Prob. 21E Ch. 5.6 - Prob. 22E Ch. 5.6 - Prob. 23E Ch. 5.6 - Prob. 24E Ch. 5.6 - Prob. 25E Ch. 5.6 - Prob. 26E Ch. 5.6 - A Bobbing Cork A cork floating in a lake is...Ch. 5.6 - FM Radio Signals The carrier wave for an FM radio...Ch. 5.6 - Blood Pressure Each time your heart beats, your...Ch. 5.6 - Predator Population Model In a predator/prey...Ch. 5.6 - Prob. 31E Ch. 5.6 - Tides The graph shows the variation of the water...Ch. 5.6 - Tides The Bay of Fundy in Nova Scotia has the...Ch. 5.6 - Prob. 34E Ch. 5.6 - Prob. 35E Ch. 5.6 - Prob. 36E Ch. 5.6 - Ferris Wheel A Ferris wheel has a radius of 10 m,...Ch. 5.6 - Cock Pendulum The pendulum in a grandfather clock...Ch. 5.6 - Variable Stars The variable star Zeta Gemini has a...Ch. 5.6 - Variable Stars Astronomers believe that the radius...Ch. 5.6 - Biological Clocks Circadian rhythms are biological...Ch. 5.6 - Electric Generator The armature in an electric...Ch. 5.6 - Electric Generator The graph shows an oscilloscope...Ch. 5.6 - Doppler Effect When a car with its horn blowing...Ch. 5.6 - Motion of a Building A strong gust of wind strikes...Ch. 5.6 - Shock Absorber When a car hits a certain bump on...Ch. 5.6 - Tuning Fork A tuning fork is struck and oscillates...Ch. 5.6 - Guitar String A guitar string is pulled at point P...Ch. 5 - Prob. 1RCC Ch. 5 - Prob. 2RCC Ch. 5 - Prob. 3RCC Ch. 5 - Prob. 4RCC Ch. 5 - Prob. 5RCC Ch. 5 - Prob. 6RCC Ch. 5 - Prob. 7RCC Ch. 5 - Prob. 8RCC Ch. 5 - Prob. 9RCC Ch. 5 - Prob. 10RCC Ch. 5 - Prob. 11RCC Ch. 5 - Prob. 12RCC Ch. 5 - Prob. 1RE Ch. 5 - Prob. 2RE Ch. 5 - Prob. 3RE Ch. 5 - Prob. 4RE Ch. 5 - Prob. 5RE Ch. 5 - Prob. 6RE Ch. 5 - Prob. 7RE Ch. 5 - Prob. 8RE Ch. 5 - Prob. 9RE Ch. 5 - Prob. 10RE Ch. 5 - Prob. 11RE Ch. 5 - Prob. 12RE Ch. 5 - Prob. 13RE Ch. 5 - Prob. 14RE Ch. 5 - Prob. 15RE Ch. 5 - Prob. 16RE Ch. 5 - Prob. 17RE Ch. 5 - Prob. 18RE Ch. 5 - Prob. 19RE Ch. 5 - Prob. 20RE Ch. 5 - Prob. 21RE Ch. 5 - Prob. 22RE Ch. 5 - Prob. 23RE Ch. 5 - Prob. 24RE Ch. 5 - Prob. 25RE Ch. 5 - Prob. 26RE Ch. 5 - Prob. 27RE Ch. 5 - Prob. 28RE Ch. 5 - Prob. 29RE Ch. 5 - Prob. 30RE Ch. 5 - Prob. 31RE Ch. 5 - Prob. 32RE Ch. 5 - Prob. 33RE Ch. 5 - Prob. 34RE Ch. 5 - Prob. 35RE Ch. 5 - Prob. 36RE Ch. 5 - Prob. 37RE Ch. 5 - Prob. 38RE Ch. 5 - Prob. 39RE Ch. 5 - Prob. 40RE Ch. 5 - Prob. 41RE Ch. 5 - Prob. 42RE Ch. 5 - Prob. 43RE Ch. 5 - Prob. 44RE Ch. 5 - Prob. 45RE Ch. 5 - Prob. 46RE Ch. 5 - Prob. 47RE Ch. 5 - Prob. 48RE Ch. 5 - Prob. 49RE Ch. 5 - Prob. 50RE Ch. 5 - Prob. 51RE Ch. 5 - Prob. 52RE Ch. 5 - Prob. 53RE Ch. 5 - Prob. 54RE Ch. 5 - Prob. 55RE Ch. 5 - Prob. 56RE Ch. 5 - Prob. 57RE Ch. 5 - Prob. 58RE Ch. 5 - Prob. 59RE Ch. 5 - Prob. 60RE Ch. 5 - Prob. 61RE Ch. 5 - Prob. 62RE Ch. 5 - Prob. 63RE Ch. 5 - Prob. 64RE Ch. 5 - Prob. 65RE Ch. 5 - Prob. 66RE Ch. 5 - Prob. 67RE Ch. 5 - Prob. 68RE Ch. 5 - Prob. 69RE Ch. 5 - Prob. 70RE Ch. 5 - Prob. 71RE Ch. 5 - Prob. 72RE Ch. 5 - Prob. 1T Ch. 5 - The point P in the figure at the left has...Ch. 5 - Prob. 3T Ch. 5 - Express tan t in terms of sin t, if the terminal...Ch. 5 - If cost=817 and if the terminal point determined...Ch. 5 - Prob. 6T Ch. 5 - Prob. 7T Ch. 5 - Prob. 8T Ch. 5 - Prob. 9T Ch. 5 - Prob. 10T Ch. 5 - The graph shown at left is one period of a...Ch. 5 - Prob. 12T Ch. 5 - A mass suspended from a spring oscillates in...Ch. 5 - An object is moving up and down in damped harmonic...Ch. 5 - Prob. 1P Ch. 5 - Prob. 2P Ch. 5 - Prob. 3P Ch. 5 - Prob. 4P Ch. 5 - Prob. 5P Ch. 5 - Prob. 6P Ch. 5 - Prob. 7P Ch. 5 - Prob. 8P Ch. 5 - Prob. 9P

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.