Chapter 4.3, Problem 33PPS

(a)

To determine

To Write: The conditional statement that shows the relationship between the areas of a pair of congruent triangles.

Answer to Problem 33PPS

If triangles are congruent, then they have the same area.

Explanation of Solution

Given information: The given statement is “the areas of congruent triangles are equal”.

As we know that congruent triangles have the same sides and equal three angles.

Therefore, the two triangles will have the same area.

Hence, the conditional statement is ‘If triangles are congruent, then they have the same area’.

(b)

To determine

To explain: Whether the converse of conditional statement is true or false.

Answer to Problem 33PPS

The converse condition of conditional statement is false.

Explanation of Solution

Given information: If triangles are congruent, then they have the same area.

The converse of the conditional statement ‘If triangles are congruent, then they have the same area’ is ‘the triangles have the same area when they are congruent’.

We can see that these are false because two triangles can have the same area but can’t be congruent, depicted below.

  

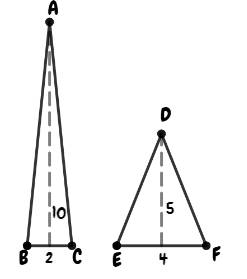
Area of the first triangle,

  $\begin{array}{l}{A}_1=\frac{1}{2}\times Va\times a_1\\ A_1=\frac{1}{2}\times 10\times 2\\ A_1=10\end{array}$

Area of the second triangle,

  $\begin{array}{l}{A}_2=\frac{1}{2}\times Vd\times a_2\\ A_2=\frac{1}{2}\times 10\times 2\\ A_2=10\end{array}$

Thus, $A_1=A_2$ but $\Delta ABC\cancel{\cong }\Delta DEF$

(c)

To determine

To explain: The possibility of two equilateral triangles can have the same area but are not congruent.

Answer to Problem 33PPS

It is impossible to have two non congruent equilateral triangles with the same areas.

Explanation of Solution

Given information: Two equilateral triangles are given.

Two non congruent triangles can’t have the same area because their side’s length and angles not equal.

(d)

To determine

To explain: The possibility of two rectangles can have the same area but are not congruent.

Answer to Problem 33PPS

Yes! It is possible to have two non congruent rectangles with the same area.

Explanation of Solution

Given information: Two non congruent rectangles are given.

Two non congruent triangles can have the same area.

  

  $\begin{array}{l}{A}_1=6\times 5\\ A_1=30\end{array}$ and $\begin{array}{l}{A}_2=3\times 10\\ A_2=30\end{array}$

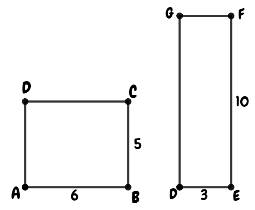
But, we can see from the sketch that sides are not congruent.

Therefore, $A_1=A_2\&ABCD\cancel{\cong }DEFG$

(e)

To determine

To explain: The possibility of two squares can have the same area but are not congruent.

Answer to Problem 33PPS

No! It is not possible to have two non congruent squares with the same area.

Explanation of Solution

Given information: Two non congruent squares are given.

Two non congruent squares can’t have the same area.

As we know, $A=s^2$

Where, s is side of square.

If the sides of the squares are equal, then its area will be equal. In this condition, its sides also become congruent.

Hence, it is not possible to draw two non congruent squares with the same area.

(f)

To determine

To find: The polygon for which the conditional statement and its converse both be true.

Answer to Problem 33PPS

The given conditional statement is valid for regular polygons.

Explanation of Solution

Given information: The conditional statement is given, If a pair of ……. Are congruent, then they have the same area.

The given condition will be true only for equilateral triangle, squares and shapes that have all sides of the same length.

Therefore, we can say that it is valid for regular polygon.