Chapter 3.7, Problem 44E

To determine

To find the intercept, asymptotes, domain, range and sketch the graph of the rational function.

Answer to Problem 44E

The rational function has $x$ -intercept is $\frac{1}{2}$ , $y$ -intercept is $\frac{1}{3}$ , vertical asymptote is $x=-\frac{3}{2}$ , horizontal asymptote is $y=-1$ , domain is $\left\{x|x\ne -\frac{3}{2}\right\}$ and range is $\left\{y|y\ne -1\right\}$ .

Explanation of Solution

Given information :

The rational function is $r\left(x\right)=\frac{1-2x}{2x+3}$

Calculation:

Intercept:

The $x$ -intercept are the zeros of the numerator,

  $\begin{array}{l}1-2x=0\\ 2x=1\\ x=\frac{1}{2}\end{array}$

So, $x$ -intercept is $\frac{1}{2}$ .

To find $y$ -intercept, substitute $x=0$ into original form of the function,

  $\begin{array}{l}r\left(0\right)=\frac{1-2\left(0\right)}{2\left(0\right)+3}\\ r\left(0\right)=\frac{1}{3}\end{array}$

The $y$ -intercept is $\frac{1}{3}$ .

Vertical asymptote:

The vertical asymptote occurs where the denominator is 0, that is, where the function is undefined.

  $\begin{array}{l}2x+3=0\\ 2x=-3\\ x=-\frac{3}{2}\end{array}$

The vertical asymptote is a line $x=-\frac{3}{2}$ .

Horizontal asymptote:

Here, the degree of the numerator is $n=1$ and denominator is $m=1$ .

Since, $n=m$ ,

Therefore,

  $\frac{\text{leading coefficient of numerator}}{\text{leading coefficient of denominator}}=\frac{-2}{2}=-1$

So, the horizontal asymptote is the line $y=-1$ .

Use the above information together with some additional values which is show in table below to sketch the graph:

$x$	$r\left(x\right)$
$-18$	$-5.3$
$-12$	$-8$
$-6$	$22$
$6$	$-1.1$
$12$	$-1.7$
$18$	$-2$

The graph is obtained as:

  

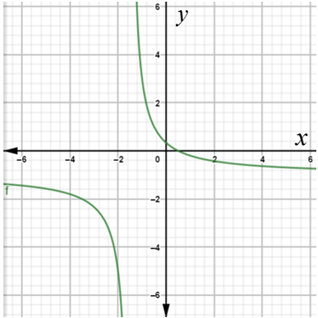
From the above graph, it can be observed that the domain of the rational function is $\left\{x|x\ne -\frac{3}{2}\right\}$ and range is $\left\{y|y\ne -1\right\}$ .

To check the result graph the rational function using graphing calculator,

  

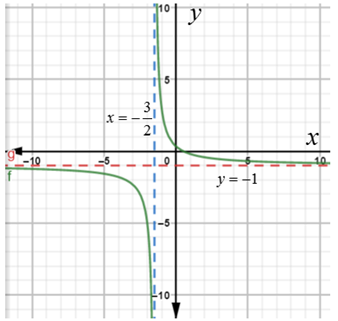
Hence,

The rational function has $x$ -intercept is $\frac{1}{2}$ , $y$ -intercept is $\frac{1}{3}$ , vertical asymptote is $x=-\frac{3}{2}$ , horizontal asymptote is $y=-1$ , domain is $\left\{x|x\ne -\frac{3}{2}\right\}$ and range is $\left\{y|y\ne -1\right\}$ .