
Concept explainers
A converging lens has a focal length of 10.0 cm. Construct accurate ray diagrams for object distances of (i) 20.0 cm and (ii) 5.00 cm. (a) From your ray diagrams, determine the location of each image. (b) Is the image real or virtual? (c) Is the image upright or inverted? (d) What is the magnification of the image? (c) Compare your results with the values found algebraically. (f) Comment on difficulties in constructing the graph that could lead to differences between the graphical and algebraic answers.
(i)
To draw: The ray diagram for the given focal lengthy of the lens and the given object distance.
Answer to Problem 36.44P
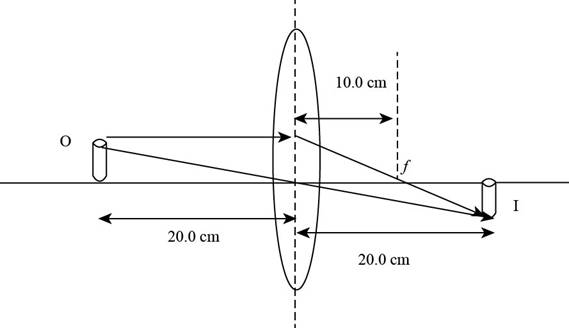
Explanation of Solution
Introduction:
In a ray diagram in the case of lens or mirror the image is formed where two at least refracted or reflected rays coincide with each other.
Explanation:
Given info: The position of object is at
The ray diagram is shown in the figure below.
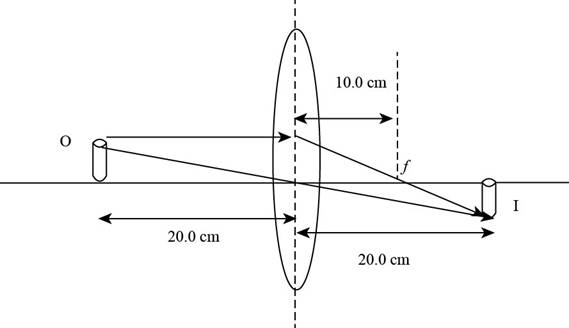
Figure (1)
(ii)
To draw: The ray diagram for the given focal length of the lens and the given object distance.
Answer to Problem 36.44P
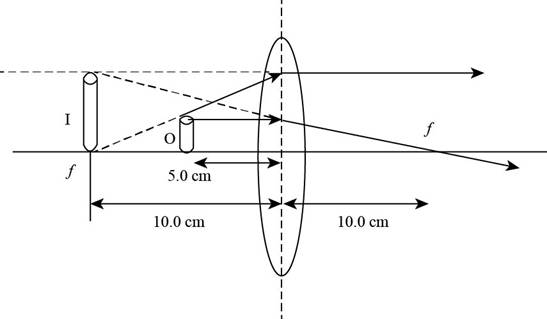
Explanation of Solution
Introduction:
In a ray diagram in the case of lens or mirror the image is formed where two at least refracted or reflected rays coincide with each other.
Explanation:
Given info: The position of object is at
The ray diagram is shown in the figure below.
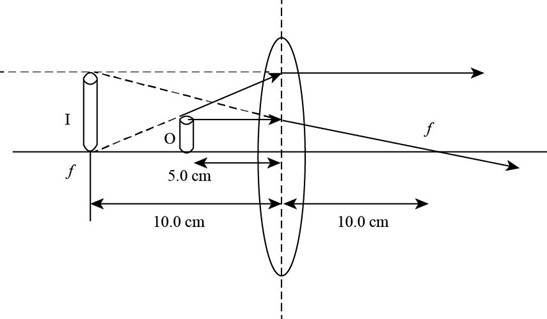
Figure (2)
(a)
Answer to Problem 36.44P
Explanation of Solution
From Figure (1), it is evident that the image is formed on the rear end of the lens and the image distance measured is
From Figure (2), the image is formed at
Conclusion:
Therefore, the measured distance for the image for the case when object is at
(b)
Answer to Problem 36.44P
Explanation of Solution
From Figure (1), it is evident that the image is formed on the rear side and is real and the images formed at the back side of the lens are real.
From Figure (2), the image is formed at
Conclusion:
The images formed by the lens in front of it are virtual and erect and images formed on the back side are real and inverted. Hence, image formed by the object kept at.
(c)
Answer to Problem 36.44P
Explanation of Solution
From Figure (1), it is evident that the image is formed on the rear side and is real. and
the real images are always inverted
From Figure (2), the image is formed at
The virtual images are always upright.
Conclusion:
Therefore, the images formed by the lens in front of it are virtual and erect and images formed on the back side are real and inverted. Hence, image formed by the object kept at.
(d)
Answer to Problem 36.44P
Explanation of Solution
Formula to calculate the magnification is
For the object at
For the object at the distance of
Conclusion:
Therefore, for the case of object at
(e)
Answer to Problem 36.44P
Explanation of Solution
Given Info: The focal length of the give lens is
From Figure (1) the image distance for the object at
For algebraic calculation, the formula for the image distance is,
Here,
Substitute
Form figure (1) the magnification is
Formula to calculate the magnification of the image
Here
Substitute
From figure (2) the image distance is
From equation (4) formula to calculate the image distance is,
Substitute
The image distance is
From equation (6) the formula to calculate the magnification is,
Substitute
From equation (6) and equation (7) it is evident that for the case of object at
From equation (8) and (9) the image distance and magnification is same for the ray diagram and the algebraic case when the object is
Conclusion:
Therefore, the result for the ray diagrams and algebraic calculations are same.
(f)
Answer to Problem 36.44P
Explanation of Solution
While drawing the graph the possible errors are human hand errors, parallax errors and scale measurement errors.
Human Hand Errors are while making the ray diagrams the rays might not converge with extreme precision. Parallax error/Human eye errors occur due to human eye. Scale errors are during the scale measurement.
Conclusion:
Therefore, the three most common errors that can lead to difficulties in constructing the graph which might lead to change the algebraic and graphical values are human hand errors, parallax errors and Scale errors.
Want to see more full solutions like this?
Chapter 36 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- A lamp of height S cm is placed 40 cm in front of a converging lens of focal length 20 cm. There is a plane mirror 15 cm behind the lens. Where would you find the image when you look in the mirror?arrow_forward(i) When an image of an object is formed by a converging lens, which of the following statements is always true? More than one statement may be correct. (a) The image is virtual. (b) The image is real. (c) The image is upright. (d) The image is inverted. (e) None of those statements is always true. (ii) When the image of an object is formed by a diverging lens, which of the statements is always true?arrow_forwardTwo converging lenses having focal lengths of f1 = 10.0 cm and f2 = 20.0 cm are placed a distance d = 50.0 cm apart as shown in Figure P35.48. The image due to light passing through both lenses is to be located between the lenses at the position x = 31.0 cm indicated. (a) At what value of p should the object be positioned to the left of the first lens? (b) What is the magnification of the final image? (c) Is the final image upright or inverted? (d) Is the final image real or virtual?arrow_forward
- The left face of a biconvex lens has a radius of curvature of magnitude 12.0 cm, and the right face has a radius of curvature of magnitude 18.0 cm. The index of refraction of the glass is 1.44. (a) Calculate the focal length of the lens for light incident from the left. (b) What If? After the lens is turned around to interchange the radii of curvature of the two faces, calculate the focal length of the lens for light incident from the left.arrow_forwardIn Figure P35.30, a thin converging lens of focal length 14.0 cm forms an image of the square abed, which is he = hb = 10.0 cm high and lies between distances of pd = 20.0 cm and pa = 30.0 cm from the lens. Let a, b, c. and d represent the respective corners of the image. Let qa represent the image distance for points a and b, qd represent the image distance for points c and d, hb, represent the distance from point b to the axis, and hc represent the height of c. (a) Find qa, qd, hb, and hc. (b) Make a sketch of the image. (c) The area of the object is 100 cm2. By carrying out the following steps, you will evaluate the area of the image. Let q represent the image distance of any point between a and d, for which the object distance is p. Let h represent the distance from the axis to the point at the edge of the image between b and c at image distance q. Demonstrate that h=10.0q(114.01q) where h and q are in centimeters. (d) Explain why the geometric area of the image is given by qaqdhdq (e) Carry out the integration to find the area of the image. Figure P35.30arrow_forwardHow far should you hold a 2.1 cm-focal length magnifying glass from an object to obtain a magnification of 10 x ? Assume you place your eye 5.0 cm from the magnifying glass.arrow_forward
- You view an object by holding a 2.5 cm-focal length magnifying glass 10 cm away from it. How far from your eye should you hold the magnifying glass to obtain a magnification of 10 ?arrow_forwardAn amoeba is 0.305 cm away from the 0.300 cm- focal length objective lens of a microscope. (a) Where is the image formed by the objective lens? (b) What is this image’s magnification? (C) An eyepiece with a 2.00-cm focal length is placed 20.0 cm from the objective. Where is the final image? (d) What angular magnification is produced by the eyepiece? (e) What is the overall magnification? (See Figure 2.39.)arrow_forwardA converging lens has a focal length of 20.0 cm. Locate the image for object distances of (a) 40.0 cm, (b) 20.0 cm, and (c) 10.0 cm. For each case, state whether the image is real or virtual and upright or inverted. Find the magnification in each case.arrow_forward
- What is the angular size of the Moon if viewed from a binocular that has a focal length of 1.2 cm for the eyepiece and a focal length of 8 cm for the objective? Use the radius of the moon 1.74106 m and the distance of the moon from the observer to be 3.8108m .arrow_forwardTwo thin lenses of focal lengths f1 = 15.0 and f2 = 10.0 cm, respectively, are separated by 35.0 cm along a common axis. The f1 lens is located to the left of the f2 lens. An object is now placed 50.0 cm to the left of the f1 lens, and a final image due to light passing though both lenses forms. By what factor is the final image different in size from the object? (a) 0.600 (b) 1.20 (c) 2.40 (d) 3.60 (e) none of those answersarrow_forwardWhat is the magnification of a magnifying lens with a focal length of 10 cm if it is held 3.0 cm from the eye and the object is 12 cm from the eye?arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





